惹某人de集训第4周学习摘录（习题+感悟）

（一）课堂内容

创建二叉树

根据先序遍历和中序遍历建树输出后序遍历

后面例题中有类似延伸（根据二叉树的中序遍历和按层遍历输出先序遍历等等）
注：任何一棵二叉树都可以根据中序遍历+先序遍历/后序遍历/层序遍历来构建

#include 
using namespace std;
const int N = 1000 + 5;
int pre[N],in[N],post[N];	//先序，中序，后序 
int idx = 0;				//遍历数组下标的位置 
struct node{
	int value;			//结点的值
	node *left,*right;	//结点的左子树和右子树 
	//构造函数，初始化 
	node(int v = 0,node *l = NULL,node *r = NULL){
		value = v;
		left = l;
		right = r;
	} 
};
//创建二叉树
void build(int left,int right,int& layer,node* &tree); 
//后序遍历
void postOrder(node *root);
//先序遍历
void preOrder(node *root);
//中序遍历
void inOrder(node *root);
//删树
void remove(node *root); 

int main(){
//	freopen("data.in","r",stdin); 
	int n;
	while(cin >> n){
		//1.读入数据
		//1)先序遍历的数据读入pre数组 
		for(int i = 0;i < n;i++)
			cin >> pre[i];
		//2)中序遍历的数据读入in数组 
		for(int i = 0;i < n;i++)
			cin >> in[i];	 
		//2.建树
		node *root; 		//定义树根结点 
	//	cout << root -> value;
		int t = 1;			//树根的层次为1 
		build(0,n - 1,t,root); 
		//3.后序遍历 
		idx = 0; 
		postOrder(root);
		//4.输出数据 
		for(int i = 0;i < n - 1;i++)
			cout << post[i] << " ";
		cout << post[n - 1] << endl;
		/*测试代码 
		//4.先序遍历-测试 
		preOrder(root);
		cout << endl;			
		//5.中序遍历-测试
		inOrder(root);
		cout << endl; 
		*/
		remove(root);	//释放内存 
	}
	return 0;
}

//创建二叉树
void build(int left,int right,int& layer,node* &tree)
{
	//1.在先序遍历中找到树根结点pre[layer - 1] 
	int t = pre[layer - 1];
	//2.在中序遍历中找到树根的位置pos,初始化为-1 
	int pos = -1; 
	for(int i = left;i <= right;i++){
		if(in[i] == t){	//找到树根 
			pos = i;	//记录树根的位置 
			break; 
		}
	} 
	//3.如果没找到，直接结束
	if(pos == -1)	return; 
	//4.创建树根结点
	tree = new node(t);	
	//中间输出
//	printf("layer:%d,pos:%d,root:%d,left:%d,right:%d\n",layer,pos,tree -> value,left,right); 	
	layer++;		//层次加1 
	//5.创建左子树[left,pos - 1]
	if(left < pos)
		build(left,pos - 1,layer,tree -> left); 
	//6.创建右子树[pos + 1,right]
	if(right > pos)
		build(pos + 1,right,layer,tree -> right); 
} 
//后序遍历
void postOrder(node *root)
{
	if(root == NULL)	return;	//递归出口
	postOrder(root -> left);	//左子树
	postOrder(root -> right);	//右子树
	post[idx++] = root -> value;//保存树根 
//	cout << root -> value << " "; 
} 

//先序遍历
void preOrder(node *root)
{
	if(root == NULL)	return;	//递归出口	
	cout << root -> value << " ";//树根 
	preOrder(root -> left);		//左子树
	preOrder(root -> right);	//右子树
} 

//中序遍历
void inOrder(node *root)
{
	if(root == NULL)	return;	//递归出口	
	inOrder(root -> left);		//左子树	
	cout << root -> value << " ";//树根 
	inOrder(root -> right);	//右子树
} 

//删树 
void remove(node *root)
{
	if(root == NULL)	
		return; 
	remove(root -> left);	//删除左子树 
	remove(root -> right);	//删除右子树 
	delete root;			//删除树根 
} 

贪心！贪心！

归并排序经典题

题目描述

天宝想做一项问卷调查，为了调查的客观性，他先用计算机生成了N（N≤100）个1000以内的随机正整数，重复的数字只保留一个，随机数与学号一一对应，然后再把这些数从小到大排序，按照排好的顺序去找同学做调查。请你帮天宝完成“去重”与“排序”的工作。

Input

    输入有2行，第1行为正整数N（N≤100），第2行为N个用空格隔开的正整数x（x≤1000），表示生成的N个随机数。

Output

    输出有2行，第1行输出去重后的随机正整数个数，第2行为升序排列的随机数，中间用空格隔开。

Sample Input

10
20 40 32 67 40 20 89 300 400 15

Sample Output

8
15 20 32 40 67 89 300 400

AC代码

#include
using namespace std;
const int N = 100 + 5;
//归并排序,对数组a[ns,ne]进行归并排序  
void mergeSort(int a[],int ns,int ne){
    //1.递归分解 
    //1)递归出口,分到只有1个数 
    if(ns == ne - 1)
        return; 
    //2)分解 ,一分为二 
    //2.1 取中点 
    int m = ns + ((ne - ns) >> 1);
    //2.2左半区间[ns,m)进行归并排序 
    mergeSort(a,ns,m); 
    //2.2右半区间[m,ne)进行归并排序 
    mergeSort(a,m,ne);
    //2. 2个有序数组的合并 
    //1)新开一个ne-ns临时空间 
    int *temp = new int[ne - ns];
    //2)开始[ns,m)和[m,ne)合并后存入temp
    int i = ns,j = m,n = 0; //左指针ns,右指针ne,临时指针n 
    while(i < m && j < ne){
        if(a[i] < a[j]){ 
            temp[n] = a[i];
            i++; //左指针右移 
        }
        else{
            temp[n] = a[j];
            j++; //右指针右移 
        }
        n++; //临时指针右移 
    }
    while(i < m) temp[n++] = a[i++]; //左边没取完 
    while(j < ne) temp[n++] = a[j++]; //右边没取完 
    for(int i = ns;i < ne;i++){
        a[i] = temp[i - ns];
    } 
    delete[] temp; 
} 
int main(){
    int n;
    cin >> n;
    int a[N];
    for(int i = 0;i < n;i++){
        cin >> a[i];
    }
    mergeSort(a,0,n);
    int sum = 1;
    for(int i = 1;i < n;i++){
        if(a[i]!=a[i-1]) sum++;
    }
    cout << sum << endl << a[0];
    for(int i = 1;i < n;i++)
        if(a[i]!=a[i-1])
            cout << " " << a[i] ;
    cout << endl;
    return 0;
}

求逆序对

题目描述

给定一个序列a1,a2,…,an，如果存在iaj，那么我们称之为逆序对，求逆序对的数目。
注意：n<=105，ai<=105

Input

第一行为n,表示序列长度。
接下来的n行，第i+1行表示序列中的第i个数。

Output

所有逆序对总数。

Sample Input

4
3
2
3
2

Sample Output

3

理解

其实这题就是对归并排序的一个考察，通过归并排序的次数来得知逆序对的数量

AC代码

#include
using namespace std;
int n;
long long ans = 0;
int a[100005],temp[100005];
//归并排序 
void merge(int l,int m,int r){
    int i = l,k = l,j = m + 1;
    while(i <= m && j <= r){
        if(a[i] <= a[j]) temp[k++] = a[i++];
        else{
            temp[k++] = a[j++];
            ans += m - i + 1;
        }
    }
    while(i <= m) temp[k++] = a[i++];
    while(j <= r) temp[k++] = a[j++];
    for(int i = l;i <= r;i++) a[i] = temp[i];
}
 
void mergesort(int l,int r){
    if(l < r){
        int mid = l + (r - l)/2;
        mergesort(l,mid);
        mergesort(mid+1,r);
        merge(l,mid,r);
    }
}
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++) cin >> a[i];
    mergesort(1,n);
    printf("%lld",ans);
    return 0; 
}

Huffman 树 Entropy POJ - 1521

题目描述

An entropy encoder is a data encoding method that achieves lossless data compression by encoding a message with “wasted” or “extra” information removed. In other words, entropy encoding removes information that was not necessary in the first place to accurately encode the message. A high degree of entropy implies a message with a great deal of wasted information; english text encoded in ASCII is an example of a message type that has very high entropy. Already compressed messages, such as JPEG graphics or ZIP archives, have very little entropy and do not benefit from further attempts at entropy encoding.
English text encoded in ASCII has a high degree of entropy because all characters are encoded using the same number of bits, eight. It is a known fact that the letters E, L, N, R, S and T occur at a considerably higher frequency than do most other letters in english text. If a way could be found to encode just these letters with four bits, then the new encoding would be smaller, would contain all the original information, and would have less entropy. ASCII uses a fixed number of bits for a reason, however: it’s easy, since one is always dealing with a fixed number of bits to represent each possible glyph or character. How would an encoding scheme that used four bits for the above letters be able to distinguish between the four-bit codes and eight-bit codes? This seemingly difficult problem is solved using what is known as a “prefix-free variable-length” encoding.
In such an encoding, any number of bits can be used to represent any glyph, and glyphs not present in the message are simply not encoded. However, in order to be able to recover the information, no bit pattern that encodes a glyph is allowed to be the prefix of any other encoding bit pattern. This allows the encoded bitstream to be read bit by bit, and whenever a set of bits is encountered that represents a glyph, that glyph can be decoded. If the prefix-free constraint was not enforced, then such a decoding would be impossible.
Consider the text “AAAAABCD”. Using ASCII, encoding this would require 64 bits. If, instead, we encode “A” with the bit pattern “00”, “B” with “01”, “C” with “10”, and “D” with “11” then we can encode this text in only 16 bits; the resulting bit pattern would be “0000000000011011”. This is still a fixed-length encoding, however; we’re using two bits per glyph instead of eight. Since the glyph “A” occurs with greater frequency, could we do better by encoding it with fewer bits? In fact we can, but in order to maintain a prefix-free encoding, some of the other bit patterns will become longer than two bits. An optimal encoding is to encode “A” with “0”, “B” with “10”, “C” with “110”, and “D” with “111”. (This is clearly not the only optimal encoding, as it is obvious that the encodings for B, C and D could be interchanged freely for any given encoding without increasing the size of the final encoded message.) Using this encoding, the message encodes in only 13 bits to “0000010110111”, a compression ratio of 4.9 to 1 (that is, each bit in the final encoded message represents as much information as did 4.9 bits in the original encoding). Read through this bit pattern from left to right and you’ll see that the prefix-free encoding makes it simple to decode this into the original text even though the codes have varying bit lengths.
As a second example, consider the text “THE CAT IN THE HAT”. In this text, the letter “T” and the space character both occur with the highest frequency, so they will clearly have the shortest encoding bit patterns in an optimal encoding. The letters “C”, "I’ and “N” only occur once, however, so they will have the longest codes.
There are many possible sets of prefix-free variable-length bit patterns that would yield the optimal encoding, that is, that would allow the text to be encoded in the fewest number of bits. One such optimal encoding is to encode spaces with “00”, “A” with “100”, “C” with “1110”, “E” with “1111”, “H” with “110”, “I” with “1010”, “N” with “1011” and “T” with “01”. The optimal encoding therefore requires only 51 bits compared to the 144 that would be necessary to encode the message with 8-bit ASCII encoding, a compression ratio of 2.8 to 1.

Input

The input file will contain a list of text strings, one per line. The text strings will consist only of uppercase alphanumeric characters and underscores (which are used in place of spaces). The end of the input will be signalled by a line containing only the word “END” as the text string. This line should not be processed.

Output

For each text string in the input, output the length in bits of the 8-bit ASCII encoding, the length in bits of an optimal prefix-free variable-length encoding, and the compression ratio accurate to one decimal point.

Sample Input

AAAAABCD
THE_CAT_IN_THE_HAT
END

Sample Output

64 13 4.9
144 51 2.8

理解

WA了好多次因为没有考虑AAAA这样子的情况，特判一下即可。

AC代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int N = 330 + 5;	//字符串有字母和数字构成A-Z,a-z,0-9 
struct node{
	char c;		//字符 
	int n;		//频次 
	node *left,*right;	//左子树，右子树 
	node(char c = 0,int n = 0,node *left = NULL,node *right = NULL):c(c),n(n),left(left),right(right){}
};
struct comp{
    bool operator () (node *x, node *y){
        if(x -> n != y -> n) 
			return x -> n > y -> n;
    	if(x -> left != NULL) 
			return x -> n >= y -> n;
    	if(y -> left != NULL) 
			return y -> n >= x -> n;
		return false;
    }
}; 
int a[N]; 				//统计每个字符出现的次数 
map<char,string> mp;	//保存字符串中的字符以及Huffman编码 		
//根据字符串s创建Huffman树 
void build(node* &root,string s); 	
//遍历树，求出每个字符的编码 
void dfs(node *root,string s);
void remove(node *root); 
int main(){
	string s;
	while(cin >> s){
		if(s == "END") break;
		//1.全局变量初始化 
		memset(a,0,sizeof(a));	//初始化字符统计数组为0 
		mp.clear();				//初始化Huffman编码为空
		node *root = NULL;		//定义Huffman树 
		build(root,s); 			//根据字符串s创建Huffman树 
		dfs(root,"");			//遍历树，求出每个字符的编码
		remove(root);
		int n = s.length() * 8;		//等长编码的长度
		map<char,string>::iterator it; 
		int ans = 0;
		int f = 0;
		for(int i = 0;i < 335;i++){
			if(a[i]==s.size()){
				f = 1;
				printf("%d %d %.1f\n",n,s.size(),1.0*n/s.size());
				break;
			}
		}
		if(f) continue;
		for(it = mp.begin();it != mp.end();it++)
			ans += (it -> second).length() * a[it -> first];
		printf("%d %d %.1f\n",n,ans,(float)1.0 * n / ans);
	}
	return 0;
}
void build(node* &root,string s)
{
	//1.预处理，统计字符串中都有那些字符以及每个字符出现的次数 
	for(int i = 0;i < s.length();i++)
		a[s[i]]++;
    priority_queue <node*,vector<node*>,comp> pq;	
	for(int i = 0;i < N;i++){
		if(a[i]){
			node *x = new node(i,a[i]);
			pq.push(x);
		}
	}		
	while(pq.size() > 1){
		node *n1 = pq.top();	pq.pop();
		node *n2 = pq.top();	pq.pop();	
		//创建父节点
		node *n3 = new node(0,n1 -> n + n2 -> n); 
		n3 -> left = n1;
		n3 -> right = n2;
		pq.push(n3);
	}
	root = pq.top();
}
//遍历树，求出每个字符的编码 
void dfs(node *root,string s)
{
	if(root -> left == NULL && root -> right == NULL){
		mp[root -> c] = s;
		return;
	}
	if(root -> left != NULL)  dfs(root -> left,s + "0");
	if(root -> right != NULL) dfs(root -> right,s + "1");	
}
void remove(node *root){
	if(root == NULL) 
		return;
	remove(root -> left);
	remove(root -> right);
	delete root;
} 

（二）有趣的题目

A - 二叉树遍历（中序遍历+按层遍历->先序遍历）

题目描述

    树和二叉树基本上都有先序、中序、后序、按层遍历等遍历顺序，给定中序和其它一种遍历的序列就可以确定一棵二叉树的结构。假定一棵二叉树一个结点用一个字符描述，现在给出中序和按层遍历的字符串，求该树的先序遍历字符串。

Input

    输入共两行，每行是由字母组成的字符串（一行的每个字符都是唯一的），分别表示二叉树的中序遍历和按层遍历的序列。

Output

    输出就一行，表示二叉树的先序序列

Sample Input

DBEAC
ABCDE

Sample Output

ABDEC

理解

	只要弄清楚了如何建树（详情参考课堂内容中的二叉树创建），就可以根据中序遍历+另外任意遍历建树并求出其他遍历结果。
	因为我太菜了，上课没听懂，后来还找紫妈妈帮我重新理了一遍建树的思路和构架，在此感恩一波紫妈（嘻嘻）

AC代码

#include 
using namespace std;
const int N = 1000 + 5;
string a,b;
struct node{
    char value;         //结点的值
    node *left,*right;  //结点的左子树和右子树 
    node(char v = 0,node *l = NULL,node *r = NULL){
        value = v;
        left = l;
        right = r;
    }
};
//创建二叉树
void build(int left,int right,int t,node* &tree); 
//先序遍历
void preOrder(node *root);
//删树
void remove(node *root); 
 
int main(){
    cin >> a >> b; //中序+层序 
    int n = a.size();
    node *root;         //定义树根结点 
    int t = 0; //下标从0开始 
    build(0,n - 1,t,root);
    preOrder(root);
    cout << endl;         
    remove(root);   //释放内存 
    return 0;
}
//创建二叉树
void build(int left,int right,int t,node* &tree){
    int pos;
    //1.在层序遍历中找到树根结点
    for(int i = t;i < b.size();i++){
        pos = -1; //层序 a 
        for(int j = left;j <= right;j++){ //中序 a  
            if(a[j] == b[i]){
                pos = j;
                break;
            }
        }
        if(pos != -1) break;
    }
 
    if(pos == -1)   return; //3.如果没找到，直接结束
    //4.创建树根结点
    tree = new node(a[pos]); 
    //5.创建左子树[left,pos - 1]
    if(left < pos)
        build(left,pos - 1,t + 1,tree -> left); 
    //6.创建右子树[pos + 1,right]
    if(right > pos)
        build(pos + 1,right,t + 1,tree -> right); 
} 
//先序遍历
void preOrder(node *root){
    if(root == NULL)    return; //递归出口  
    cout << root -> value;//树根 
    preOrder(root -> left);      //左子树
    preOrder(root -> right); //右子树
} 
//删树 
void remove(node *root){
    if(root == NULL)    
        return; 
    remove(root -> left);    //删除左子树 
    remove(root -> right);   //删除右子树 
    delete root;            //删除树根 
}

B - 二叉树凹入法输出

题目描述

     树的凹入表示法主要用于树的屏幕或打印输出，其表示的基本思想是兄弟间等长，一个结点要不小于其子结点的长度。二叉树也可以这样表示，假设叶结点的长度为1，一个非叶结点的长并等于它的左右子树的长度之和。
    一棵二叉树的一个结点用一个字母表示（无重复），输出时从根结点开始：
    每行输出若干个结点字符（相同字符的个数等于该结点长度），
    如果该结点有左子树就递归输出左子树；
     如果该结点有右子树就递归输出右子树。
     假定一棵二叉树一个结点用一个字符描述，现在给出先序和中序遍历的字符串，用树的凹入表示法输出该二叉树。

Input

    输入共两行，每行是由字母组成的字符串（一行的每个字符都是唯一的），分别表示二叉树的先序遍历和中序遍历的序列。

Output

    输出行数等于该树的结点数，每行的字母相同。

Sample Input

ABCDEFG
CBDAFEG

Sample Output

AAAA
BB
C
D
EE
F
G

理解

由题意可以画出这颗二叉树	，题目要求根据一个结点的子结点数来输出
所以接下来我们要做的就是！没错！还是建树！，然后dfs搜索该结点的最多有多少结点，然后存在数组里就阔以输出啦！

AC代码

#include 
using namespace std;
const int N = 1000 + 5;
string pre,in;  //先序，中序
int idx = 0;
struct node{
    char value;
    node *left,*right;
    node(char v = 0,node *l = NULL,node *r = NULL){
        value = v;
        left = l;
        right = r;
    }
};
void build(int left,int right,int& layer,node* &tree){
    //1.在先序遍历中找到树根结点pre[layer - 1] 
    int t = pre[layer - 1];
    //2.在中序遍历中找到树根的位置pos,初始化为-1 
    int pos = -1; 
    for(int i = left;i <= right;i++){
        if(in[i] == t){ //找到树根 
            pos = i;    //记录树根的位置 
            break;
        }
    } 
    if(pos == -1)   return;     //没找到，直接结束
    tree = new node(t);     //创建树根结点
    layer++;
    if(left < pos)
        build(left,pos - 1,layer,tree -> left); 
    if(right > pos)
        build(pos + 1,right,layer,tree -> right); 
}
int sum[N] = {0};
int dfs(node *root){
    if(root == NULL) return 1;
    sum[root->value -'A'] += dfs(root->left);
    sum[root->value -'A'] += dfs(root->right);
    return sum[root -> value -'A'];
}
//先序遍历
void preOrder(node *root){
    if(root == NULL) return;    //递归出口
    for(int j = 0;j < sum[root->value -'A']/2;j++){
        cout << root -> value;
    }
    cout << endl; 
    preOrder(root -> left);      //左子树
    preOrder(root -> right); //右子树
} 
//删树 
void remove(node *root){
    if(root == NULL) return; 
    remove(root -> left);    //删除左子树 
    remove(root -> right);   //删除右子树 
    delete root;            //删除树根 
}
int main(){
    cin >> pre >> in;    
    int n = in.size();
    //2.建树
    node *root;         //定义树根结点 
    int t = 1;          //树根的层次为1 
    build(0,n - 1,t,root);
    dfs(root);
    preOrder(root);
    remove(root);   //释放内存 
    return 0;
}

C - FBI树

题目描述

     我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。
     FBI树是一种二叉树[ 二叉树：二叉树是结点的有限集合，这个集合或为空集，或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。]，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：
    T的根结点为R，其类型与串S的类型相同；
    若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。
    现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历。

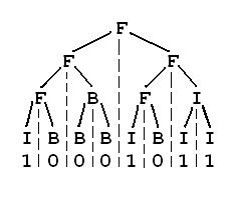
Input

    输入的第一行是一个整数N（0 <= N <= 10），第二行是一个长度为2N的“01”串。

Output

    输出包括一行，这一行只包含一个字符串，即FBI树的后序遍历序列。

Sample Input

3
10001011

Sample Output

IBFBBBFIBFIIIFF

理解

FBI树实质上就是一个从二叉树子结点推导父节点的过程。
就以样例来说，最小的子结点为10001011，1 -> i ,0 -> B 
当一个节点的两个子结点为 i 和 B 时 他的父节点为F，当一个节点的两个子结点为 B 和 B 时 他的父节点为B，当一个节点的两个子结点为 i 和 i 时 他的父节点为i。
由此一步一步递推即可，当该节点没有父节点时，说明已经找到了根

AC代码

#include 
using namespace std;
int ans = 1;
string s;
int tree[10010] = {0};
int FBI(int begin,int end){
    int mid = (begin + end)/2; //中间对半分 
    if(begin == end){ //只剩一个字母了
        tree[++ans] = s[begin];
        return ans;
    }
    int L = FBI(begin,mid); //左半段 
    int R = FBI(mid+1,end); //右半段 
    if(tree[L]==tree[R]) tree[++ans] = tree[R];
    else tree[++ans] = '2';
    return ans;
}
int main(){
    int n;
    cin >> n; 
    cin >> s;
    int l = s.size();
    if(l == 1){
        if(s[0] == '0') cout << "B";
        else cout << "I";
        return 0; 
    }
    FBI(0,l-1);
    for(int i = 1;i <= ans;i++){
        if(tree[i] == '0') cout << "B";
        if(tree[i] == '1') cout << "I";
        if(tree[i] == '2') cout << "F";
    }
    return 0;
}

D - 小球

题目描述

    许多的小球一个一个的从一棵满二叉树上掉下来组成FBT（Full Binary Tree，满二叉树），每一时间，一个正在下降的球第一个访问的是非叶子节点。然后继续下降时，或者走右子树，或者走左子树，直到访问到叶子节点。决定球运动方向的是每个节点的布尔值。最初，所有的节点都是FALSE，当访问到一个节点时，如果这个节点是FALSE，则这个球把它变成TRUE，然后从左子树走，继续它的旅程。如果节点是TRUE，则球也会改变它为FALSE，而接下来从右子树走。满二叉树的标记方法如下图。

    因为所有的节点最初为FALSE，所以第一个球将会访问节点1，节点2和节点4，转变节点的布尔值后在在节点8停止。第二个球将会访问节点1、3、6,在节点12停止。明显地，第三个球在它停止之前，会访问节点1、2、5，在节点10停止。
    现在你的任务是，给定FBT的深度D，和I，表示第I个小球下落，你可以假定I不超过给定的FBT的叶子数，写一个程序求小球停止时的叶子序号。

Input

    输入仅一行包含两个用空格隔开的整数D和I。其中2<=D<=20，1<=I<=524288。

Output

    对应输出第I个小球下落停止时的叶子序号。

Sample Input

4 2

Sample Output

12

理解

其实我用的是模拟的方法，后来又在vj遇到了这道题！
因为数字太大，模拟会tle，然后就换了个写法。后面会贴出来的。

AC代码

#include
using namespace std;
 
int main(){
    int n,ball,r;
    int y[2000005];
    cin >> n >> ball;
    memset(y,0,sizeof(y));
    for(int i = 0;i < ball;i++){
        int j = 0;
        while(j * 2 <= pow(2,n)-1){
            if(!y[j]){
                y[j] = !y[j];
                j *= 2; //往左 
            }
            else{
                y[j] = !y[j];
                j = j * 2 + 1; //往右 
            }
        }
        r = j;
    }
    cout << r << endl;
    return 0;
} 

E - 导弹拦截

题目描述

    某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统，但是这种拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，由于该系统还在试用阶段。所以一套系统有可能不能拦截所有的导弹。
     输入导弹依次飞来的高度（雷达给出的高度不大于30000的正整数）。计算要拦截所有导弹最小需要配备多少套这种导弹拦截系统。

Input

    n颗依次飞来的高度（1≤n≤1000）

Output

    要拦截所有导弹最小配备的系统数k

Sample Input

389 207 155 300 299 170 158 65

Sample Output

2

理解

提示
输入：导弹高度： 7 9 6 8 5
输出：导弹拦截系统K=2
输入：导弹高度： 4 3 2
输出：导弹拦截系统K=1
起先我理解错题意了，以为换了一个导弹前一个就不能继续接收了！
按照贪心的想法，应该是把每个系统可拦截的高度存起来，每一颗导弹来
就从头遍历一遍，若所有的系统都无法拦截则开一个新系统
15555 这题WA了好多次（哭）

AC代码

#include 
using namespace std;
const int N = 1000 + 5;
int a[N] = {0};
int high[N];
int main(){
    int n = 0; 
    while(cin >> a[n++]){}
    for(int i = 0;i < n;i++){
        high[i] = 30005;
    }
    for(int i = 0;i < n;i++){
        for(int j = 0;j <= i;j++){
            if(high[j] >= a[i]){
                high[j] = a[i];
                break;
            }
        }
    }
    int cnt = 0;
    for(int i = 0;i < n;i++){
        if(high[i] != 30005){
            cnt++;
        }
    }
    cout << cnt << endl;
}

F - 删数问题

题目描述

    输入一个高精度的正整数N，去掉其中任意S个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的N和S，寻找一种方案使得剩下的数字组成的新数最小。
输出新的正整数。（N不超过240位）输入数据均不需判错。

Input

n
s

Output

最后剩下的最小数。

Sample Input

175438
4

Sample Output

13

理解

起先我以为删掉最大的数就ok，样例看起来仿佛也就那么回事
然后果断的写完提交一气呵成，然后一个大写的WA！
后来发现并不是从前到后删除最大的数
应该是找从前往后开始递减时，最大的值

AC代码

#include 
using namespace std;
int main(){
    char a[250];
    int n,i;
    cin >> a >> n;
    int l = strlen(a);
    while(n--){
        i = 0;
        while(i<l&&a[i]<=a[i+1]){
            i++;
        }
        while(i<=l){
            a[i] = a[i+1];
            i++;
        }
        a[i+1]='\0';
        l--;
        l = strlen(a);
        while(l >1 && a[0]=='0'){
            for(int i = 0;i <= l;i++){
                a[i] = a[i+1]; 
            }
        }
        l--;
    }
    printf("%s",a);
    return 0;
} 

G - 最大整数

题目描述

    设有n个正整数（n≤20），将它们联接成一排，组成一个最大的多位整数。 例如：n=3时，3个整数13，312，343联接成的最大整数为：34331213 又如：n=4时，4个整数7，13，4，246联接成的最大整数为：7424613

Input

    输入格式如下： 第一行为正整数n，第2行为n个正整数，2个正整数之间用空格间隔。

Output

    输出n个数连接起来的最大整数

Sample Input

3
13 312 343

Sample Output

34331213

理解

这题和饭饭姐姐一起讨论了很久，自己拟了很多样例推翻了自己全部的思路类似于第一位比较等等，后来在大佬的点拨下，发现这题用字符串写更为快捷
以为c++中字符串可以直接加减然后用字典序比较大小，知道这点后题目就很简单了

AC代码

#include 
using namespace std;
 
int main(){
    int n;
    cin >> n;
    string a[n];
    for(int i = 0;i < n;i++){
        cin >> a[i];
    }
    for(int i = 1;i < n;i++){
        for(int j = 0;j < n - i;j++){
            if(a[j]+a[j+1] < a[j+1]+a[j]){
                string s;
                s = a[j];
                a[j] = a[j+1];
                a[j+1] = s;
            }
        }
    }
    for(int i = 0;i < n;i++){
        cout << a[i];
    }
    cout << endl;
    return 0;
}

H - 马克与美元

题目描述

    假期到了，天宝要学习马克与美元的汇率。请编写程序帮天宝计算一下，如何买卖马克和美元，使他从100美元开始，最后能获得最高可能的价值。

Input

     输入的第一行是一个自然数N，1≤N≤100，表示天宝学习的天数。
     接下来的N行中每行是一个自然数x，1≤x≤1000。第i+1行的x表示已知道的第i+1天的平均汇率，在这一天中，天宝既能用100美元买A马克也能用A马克购买100美元。

Output

     输出只有1行，请输出天宝获得的最大价值（美元单位，留两位小数)。
     注意：天宝必须在最后一天结束之前将他的钱都换成美元。

Sample Input

5
400
300
500
300
250

Sample Output

266.66

理解

既然是贪心！当然要考虑眼前的利益，当第二天的汇率比前一天低时，只要前一天换成马克第二天换回来就能赚钱
所以本着贪心的思想，要做到最贪，就是每当后一天比前一天低就立刻换成马克再换回来。
这样既保证了天宝手里结束时肯定是美元且肯定赚到了最大的利益。

AC代码

#include 
using namespace std;
 
int main(){
    int n;
    cin >> n;
    int a[n];
    for(int i = 0;i < n;i++){
        cin >> a[i];
    }
    double sum = 100;
    for(int i = 0;i < n-1;i++){
        if(a[i]>a[i+1]){
            sum *= (double)a[i]/a[i+1];
        }
    }
    printf("%.2lf\n",sum);
    return 0;
}

I - 胖子计划

题目描述

    Mr.L正在完成自己的增肥计划。
    为了增肥，Mr.L希望吃到更多的脂肪。然而也不能只吃高脂肪食品，那样的话就会导致缺少其他营养。Mr.L通过研究发现：真正的营养膳食规定某类食品不宜一次性吃超过若干份。比如就一顿饭来说，肉类不宜吃超过1份，鱼类不宜吃超过1份，蛋类不宜吃超过1份，蔬菜类不宜吃超过2份。Mr.L想要在营养膳食的情况下吃到更多的脂肪，当然Mr.L的食量也是有限的。

Input

    第一行包含三个正整数n（n≤200）,m（m≤100）和k（k≤100）。表示Mr.L每顿饭最多可以吃m份食品，同时有n种食品供Mr.L选择，而这n种食品分为k类。第二行包含k个不超过10的正整数，表示可以吃1到k类食品的最大份数。接下来n行每行包括2个正整数，分别表示该食品的脂肪指数ai和所属的类别bi，其中ai≤100，bi≤k。

Output

    包括一个数字即Mr.L可以吃到的最大脂肪指数和

Sample Input

6 6 3
3 3 2
15 1
15 2
10 2
15 2
10 2
5 3

Sample Output

60

理解

这题的意思就是要求得到的能量最多，所以按照食物的能量从大到小排序
当该种类食物还能吃的数量不为零时，就吃，否则就跳过
这样就可以保证在有限的数量内吃到最多的能量。

AC代码

#include 
using namespace std;
const int MAXN = 200 + 5;
struct node{
    int x,y;
}food[MAXN];
bool cmp(node a,node b){
    return a.x > b.x;
}
int main(){
    int n,m,k;
    cin >> n >> m >> k;
    int b[105];
    for(int i = 1;i <= k;i++){
        cin >> b[i];
    }
    for(int i = 1;i <= n;i++){
        cin >> food[i].x >> food[i].y;
    }
    sort(food+1,food+n+1,cmp);
    int sum = 0;
    int ans = 0;
    for(int j = 1;j <= n;j++){
        if(b[food[j].y] != 0){
            ans++;
            sum += food[j].x;
            b[food[j].y]--;
        }
        if(ans == m) break;
    }
    cout << sum << endl;
    return 0;
}

J - 一元三次方程求解

是个水题没错了，但我WA了三次！！！注意精度啊朋友们

题目描述

有形如：ax3+bx2+cx+d＝0这样的一个一元三次方程。给出该方程中各项的系数（a,b,c,d均为实数），并约定该方程存在三个不同实根（根的范围在-100至100之间），且根与根之差的绝对值≥1。
要求由小到大依次在同一行输出这三个实根（根与根之间留有空格），并精确到小数点后2位。
提示：记方程f（x）=0，若存在2个数x1和x2，且x1

Input

a，b，c，d

Output

三个实根（根与根之间留有空格）

Sample Input

1 -5 -4 20

Sample Output

-2.00 2.00 5.00

理解

首先判断找到第一个解，然后继续循环找到一个i使得f(i)*f(i+1) < 0 说明在i 到 i + 1的范围内存在一个解，然后就可以不断缩小范围来找到解

正常AC代码

#include 
using namespace std;
double a,b,c,d;
double func(double x){
    return a*x*x*x+b*x*x+c*x+d;
}
void find(double l,double r){
    if(r - l < 0.001){
        printf("%.2lf ",l);
        return;
    }
    double mid = (l+r)/2;
    if(func(mid)==0){
        printf("%.2lf ",mid);
        return;
    }
    if(func(mid)*func(l)<0) find(l,mid);
    else if(func(mid)*func(r)<0) find(mid,r);
}
int main(){
    cin >> a >> b >> c >> d;
    for(double i = -100;i <= 100;i++){
        if(func(i)==0){
            printf("%.2lf ",i);
            continue;
        }
        if(func(i)*func(i+1)<0) find(i,i+1);
    }
    return 0;
}

暴力代码（不会tle居然！）

#include 
using namespace std;
int main(){
    double a,b,c,d;
    cin >> a >> b >> c >> d;
    int f = 0;
    for(double i = -100;i <= 100;i+=0.01){
        if(abs(a*i*i*i+b*i*i+c*i+d)<=1e-6){
            if(!f){
                printf("%.2f",i);
                f = 1;
            }
            else printf(" %.2f",i);
        }
    }
    return 0;
}

K - 求逆序对

题目描述

给定一个序列a1,a2,…,an，如果存在iaj，那么我们称之为逆序对，求逆序对的数目。

注意：n<=105，ai<=105

Input

第一行为n,表示序列长度。
接下来的n行，第i+1行表示序列中的第i个数。

Output

所有逆序对总数。

Sample Input

4
3
2
3
2

Sample Output

3

理解

其实这题就是对归并排序的一个考察，通过归并排序的次数来得知逆序对的数量

AC代码

#include
using namespace std;
int n;
long long ans = 0;
int a[100005],temp[100005];
//归并排序 
void merge(int l,int m,int r){
    int i = l,k = l,j = m + 1;
    while(i <= m && j <= r){
        if(a[i] <= a[j]) temp[k++] = a[i++];
        else{
            temp[k++] = a[j++];
            ans += m - i + 1;
        }
    }
    while(i <= m) temp[k++] = a[i++];
    while(j <= r) temp[k++] = a[j++];
    for(int i = l;i <= r;i++) a[i] = temp[i];
}
 
void mergesort(int l,int r){
    if(l < r){
        int mid = l + (r - l)/2;
        mergesort(l,mid);
        mergesort(mid+1,r);
        merge(l,mid,r);
    }
}
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++) cin >> a[i];
    mergesort(1,n);
    printf("%lld",ans);
    return 0; 
}

L - 麦森数（mason）（压位做法）

题目描述

形如2P-1的素数称为麦森数，这时P一定也是个素数。但反过来不一定，即如果P是个素数，2P-1不一定也是素数。到2016年底，人们已找到了49个麦森数。

美国中央密苏里大学数学家库珀领导的研究小组通过参加一个名为“互联网梅森素数大搜索”(GIMPS)项目，于2016年1月7日发现了第49个梅森素数——274207281-1。该素数也是目前已知的最大素数，有22338618位。这是库珀教授第四次通过GIMPS项目发现新的梅森素数，刷新了他的记录。他上次发现第48个梅森素数257,885,161-1是在2013年1月，有17425170位。

梅森素数在当代具有重大意义和实用价值。它是发现已知最大素数的最有效途径，其探究推动了“数学皇后”——数论的研究，促进了计算技术、密码技术、程序设计技术和计算机检测技术的发展。难怪许多科学家认为，梅森素数的研究成果，在一定程度上反映了一个国家的科技水平。英国数学协会主席马科斯 索托伊甚至认为它的研究进展不但是人类智力发展在数学上的一种标志，也是整个科技发展的里程碑之一。

Input

    输入P（1000

Output

输出共11行。
第1行：十进制高精度数2P-1的位数；
第2-11行：十进制高精度数2P-1的最后500位数字（每行输出50位，共输出10行，不足500位时高位补0）；
不必验证2P-1与P是否为素数。

Sample Input

1279

Sample Output

386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087

理解

代码里写了注释，感恩紫妈教我的这种方法！耐心地讲了三遍（哭）

AC代码

#include 
using namespace std;
int main(){
    long long p,k;
    long long t = 10000000000;
    cin >> p;
    // 2的p次个位数:2,4,8,6(循环) 所以位数log10(2^p-1)==log10(2^p)+1==p*log10(2)+1; 
    cout << (int)(p * log10(2) + 1) << endl;
    long long a[55]={0}; //每十位看做一组存起来 ,相当于十进制改十亿进制 
    a[1] = 1;
    while(p >= 25){
        k = 0;
        for(int i = 1;i <= 50;i++){
            a[i] = (a[i] << 25) + k;
            k = a[i] / t; //大于10亿的进位 
            a[i] %= t;
        }
        p -= 25; // 每次*(1<<25) 不断更新每一个值 
    }
    k = 0;
    for(int i = 1;i <= 50;i++){
        a[i] = (a[i] << p) + k;
        k = a[i] / t;
        a[i] %= t;
    }
    a[1]--;
    int cnt = 0;
    for(int i = 50;i >= 1;i--){
        printf("%010lld",a[i]);
        cnt++;
        if(cnt == 5){
            cout << endl;
            cnt = 0;
        }
    }
    return 0;
}

M - Strange fuction HDU - 2899

题目描述

Now, here is a fuction:
F(x) = 6 * x^7+8*x6+7x^3+5*x2-yx (0 <= x <=100)
Can you find the minimum value when x is between 0 and 100.

Input

The first line of the input contains an integer T(1<=T<=100) which means the number of test cases. Then T lines follow, each line has only one real numbers Y.(0 < Y <1e10)

Output

Just the minimum value (accurate up to 4 decimal places),when x is between 0 and 100.

Sample Input

2
100
200

Sample Output

-74.4291
-178.8534

AC代码

#include 
using namespace std;
const double eps = 1e-8;
double y;
double func(double x){
	return 6*pow(x,7.0)+8*pow(x,6.0)+7*pow(x,3.0)+5*pow(x,2.0)-y*x;
}
double solve(){
	double T = 100;
	double delta = 0.98;
	double x = 50.0;
	double now = func(x);
	double ans = now;
	while(T>eps){
		int f[2]={1,-1};
		double newx = x + f[rand()%2]*T;
		if(newx >= 0 && newx <= 100){
			double next = func(newx);
			ans = min(ans,next);
			if(now - next > eps){
				x = newx;
				now = next;
			}
		}
		T *= delta;
	}
	return ans;
}
int main(){
	int cas;
	cin >> cas;
	while(cas--){
		cin >> y;
		printf("%.4f\n",solve());
	}
	return 0;
}

N - Intervals POJ - 1089

题目描述

There is given the series of n closed intervals [ai; bi], where i=1,2,…,n. The sum of those intervals may be represented as a sum of closed pairwise non−intersecting intervals. The task is to find such representation with the minimal number of intervals. The intervals of this representation should be written in the output file in acceding order. We say that the intervals [a; b] and [c; d] are in ascending order if, and only if a <= b < c <= d.
Task
Write a program which:
reads from the std input the description of the series of intervals,
computes pairwise non−intersecting intervals satisfying the conditions given above,
writes the computed intervals in ascending order into std output

Input

In the first line of input there is one integer n, 3 <= n <= 50000. This is the number of intervals. In the (i+1)−st line, 1 <= i <= n, there is a description of the interval [ai; bi] in the form of two integers ai and bi separated by a single space, which are respectively the beginning and the end of the interval,1 <= ai <= bi <= 1000000.

Output

The output should contain descriptions of all computed pairwise non−intersecting intervals. In each line should be written a description of one interval. It should be composed of two integers, separated by a single space, the beginning and the end of the interval respectively. The intervals should be written into the output in ascending order.

Sample Input

5
5 6
1 4
10 10
6 9
8 10

Sample Output

1 4
5 10

理解

这题我的方法不是优解，算是勉强AC ，一直卡tle了很久，然后把cin改成了scanf嘻嘻
谢谢学长帮我找bug，大半夜的头铁莽夫惹某人提交了五次菜A了这题

AC代码

#include 
#include 
#include 
#include 
#include 
using namespace std;
struct node{
	int start,end;
}a[50005],b[50005];
bool cmp(node a,node b){
	if(a.start == b.start) return a.end < b.end;
	return a.start < b.start;
}
int main(){
    int n;
	while(~scanf("%d",&n) && n){
		for(int i = 0;i < n;i++){
			int x,y;
			scanf("%d %d",&x,&y);
			a[i].start = x,a[i].end = y;
		}
		sort(a,a+n,cmp);
		memset(b,0,sizeof(b));
		b[0].start = a[0].start,b[0].end = a[0].end;
		for(int i = 1;i < n;i++){
			for(int j = 0;j < n;j++){
				if(b[j].start!=0){
					if(a[i].start <= b[j].end){
						if(a[i].end >= b[j].end){
							b[j].end = a[i].end;
						}
						break;					
					}
					else continue;
				}
				else{
					b[j].start = a[i].start,b[j].end = a[i].end;
					break;
				}
			}
		}
		for(int i = 0;i < n;i++){
			if(b[i].start != 0){
				printf("%d %d\n",b[i].start,b[i].end);
			}
		}
	}
    return 0;
}

（三）个人感受

本周感想

果然是头秃的一周，but！！！贪心救我狗命！贪心只要你够‘贪’，就能想到很多方法来解一题
最重要的是考虑眼前的利益。这一周难得能ak日常题集了，继续加油鸭。
这周的atcoder（题目有点水），本惹终于A了四题，嘻嘻
这次的学习摘录因为时间原因没有摘录Atcdoer和百度之星的一些题目（写周记写晚了15555）