动态规划（线性）

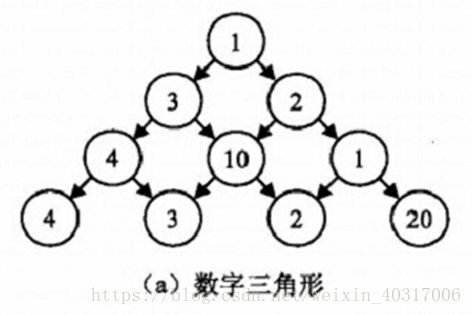
【数字三角形】

【问题】从三角形的顶至底的一条路径，使该路径经过的数字总和最大

• 方法一：递归求解

【分析】：用二维数组存放数字三角形，D( x, y) : 第x行第 y 个数字(x,y从1 开始算) , MaxSum(x,y ) : 从D(x,y)到底边的各条路径中，最佳路径的数字之和。 求 MaxSum(1,1) ,D(x, y)出发，下一步只能走D(x+1,y)或者D(x+1,yj+1)。故对于N行的三角形：

//递归
#include 
#include 
#define Max 101
using namespace std;
int D[Max][Max];
int num;
int MaxSum(int x, int y)
{
	if(x == num)             //当加到最后一行 递归结束
       return D[x][y];
    return max(MaxSum(x+1, y),MaxSum(x+1, y + 1))+ D[x][y]; //选取左孩子或者右孩子最大的那个
}
int main()
{
	int i, j;
    cin >> num;
	for(i = 1; i <= num; i ++)
       for(j = 1; j <= i; j ++)
		   cin >> D[i][j];
	cout <

• 方法二：动态规划求解

【分析】找子问题dp[i][j]：a[i][j]到第n层的最大值。自顶向下分析，从底向上递推出最后一行外，每一行的每个点的最大值等于自身加上下面一行对应左右两个点的最大值，从下往上递推，最顶部的即所求。注意边界。DP高效的原因：重叠子问题、记录子问题结果. 

#include
#define M 101
using namespace std;
int dp[M][M];
int main()
{
	int num;
	cin >> num;
	for (int i = 1; i <= num; i++)
	{
		for (int j = 1; j <= i; j++)
			cin >> dp[i][j];
	}
	for (int i = num - 1; i >= 1; i--) //从下往上找最大值加上去
	{
		for (int j = 1; j <= i; j++)
			dp[i][j] = (dp[i + 1][j], dp[i + 1][j + 1]) + dp[i][j];
	}
	cout << endl;
	for (int i =1; i<=num; i++)
	{
		for (int j = 1; j <= i; j++)
			cout << dp[i][j] << " ";
		cout << endl;
	}
    //最终答案为dp[1][1]
	return 0;
}

【最大连续序列和】

【问题】   给定一个长度为n的序列a[1],a[2]...a[n-1],a[n]，求一个连续的子序列a[i],a[i+1]...a[j-1],a[j]，使得a[i]+a[i+1]...a[j-1]+a[j]最大。

【分析】

步骤 1：令状态 dp[i] 表示以 A[i] 作为末尾的连续序列的最大和（这里是说 A[i] 必须作为连续序列的末尾）。

步骤 2：因为 dp[i] 要求是必须以 A[i] 结尾的连续序列，那么只有两种情况：

• 这个最大和的连续序列只有一个元素，即以 A[i] 开始，以 A[i] 结尾。
• 这个最大和的连续序列有多个元素，即从前面某处 A[p] 开始 (p

对第一种情况，最大和就是 A[i] 本身。 dp[i]=A[i];

对第二种情况，最大和是 dp[i-1]+A[i]。dp[i]=dp[i-1]+A[i]

于是得到状态转移方程：　dp[i] = max{A[i], dp[i-1]+A[i]}

这个式子只和 i 与 i 之前的元素有关，且边界为 dp[0] = A[0]，由此从小到大枚举 i，即可得到整个 dp 数组。接着输出 dp[0]，dp[1]，...，dp[n-1] 中的最大子即为最大连续子序列的和。

#include
#include
#include
#include
using namespace std;
int dp[200];
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> dp[i];
	int m = dp[1];
	for (int i = 2; i <= n; i++)
	{
		dp[i] = max(dp[i], dp[i] + dp[i - 1]);   //dp[i]代表，前i个元素中连续最大序列和
		if (dp[i] > m)
			m = dp[i];
	}
	cout << m << endl << endl;
	for (int i = 1; i <= n; i++)
	{
		cout << dp[i] << " ";
	}
}

 

【最长上升子序列=最长非降序子序列】

【问题】  给出一个序列a1,a2,a3,a4,a5,a6,a7....an,求它的一个子序列（设为s1,s2,...sm），使得这个子序列满足这样的性质，s1

【例子】

让我们举个例子：求 2 7 1 5 6 4 3 8 9 的最长上升子序列。我们定义d(i) (i∈[1,n])来表示前i个数以A[i]结尾的最长上升子序列长度。

前1个数 d(1)=1 子序列为2；

前2个数 7前面有2小于7 d(2)=d(1)+1=2 子序列为2 7

前3个数 在1前面没有比1更小的，1自身组成长度为1的子序列 d(3)=1 子序列为1

前4个数 5前面有2小于5 d(4)=d(1)+1=2 子序列为2 5

前5个数 6前面有2 5小于6 d(5)=d(4)+1=3 子序列为2 5 6

前6个数 4前面有2小于4 d(6)=d(1)+1=2 子序列为2 4

前7个数 3前面有2小于3 d(3)=d(1)+1=2 子序列为2 3

前8个数 8前面有2 5 6小于8 d(8)=d(5)+1=4 子序列为2 5 6 8

前9个数 9前面有2 5 6 8小于9 d(9)=d(8)+1=5 子序列为2 5 6 8 9

#include
#include
#include
using namespace std;
int main()
{
	int a[2000];
	int dp[2000];
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	dp[1]=1;        // 以第一个数结尾的最长上升子序列个数为1,设这个为最长上升子序列长度
	int mm=dp[1];
	for(int i=2;i<=n;i++)
	{
		int sum=0;       //还未开始遍历，子序列个数为0
		for(int j=1;j<=i;j++)
		{
			if(a[i]>=a[j])  //此时非递减
				sum=max(sum,dp[j]);
		}
		dp[i]=sum+1;
		if(dp[i]>mm)   //这个序列长度大于上一个最大序列长度
			mm=dp[i];
	}
	printf("%d\n",mm);
	return 0;
}

【最长子序列长度的排好序的最小序列】

https://www.cnblogs.com/GodA/p/5180560.html

【最长公共子序列】

【问题】给定两个序列X(x1,x2,x3…xm)和Y(y1, y2, y3…yn)，求长度最大的公共子序列的长度。例如：1,5,2,6,8,7 和 2,3,5,6,9,8,4 的LCS为5,6,8（另一个解是2,6,8）

公共子序列 ：

对序列 1,3,5,4,2,6,8,7和序列 1,4,8,6,7,5 来说

序列1,8,7是它们的一个公共子序列。

最长公共子序列：最长公共子序列不唯一。

1,4,8,7

1,4,6,7

【分析】Ax= a1,a2,……ax, By= b1,b2,……by, Ax、Bx分别表示序列A、B续前x项构成的子序列我们用L(x, y)表示它们的最长公共子序列长度，那原问题等价于求dp[m,n]

• Ax=By

求(Ax, By)    L(Ax, By) = L(x - 1, y - 1) + 1

• Ax ≠ By

L(x,y) = L(x – 1, y)；

LCS(x,y) = LCS(x, y – 1)；