给定两个字符串A,B,判断T是否为S的子串(变式:寻找子串B在串A中的位置)。
要求一个O(|A|+|B|)的做法。
通常称A为目标串(或主串),B为模式串。
算法过程:
我们假设串A的长度为n,串B的长度为m,每个字符串的开头下标默认为1。
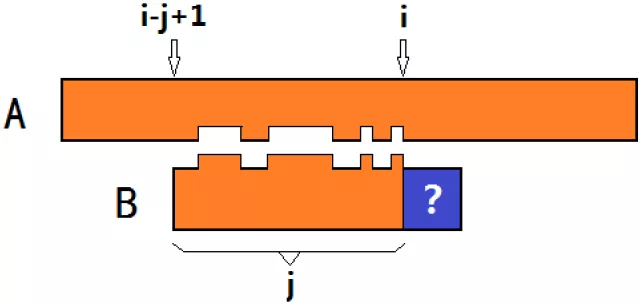
定义两个变量i和j,这两个变量共同表示:A[i-j+1~i]与B[1~j]均匹配,即:A中以第i个字符结尾的、长度为j的字符串,和B从头开始长度为j的字符串完全匹配。
继续往下匹配:如果i+1和j+1不匹配。
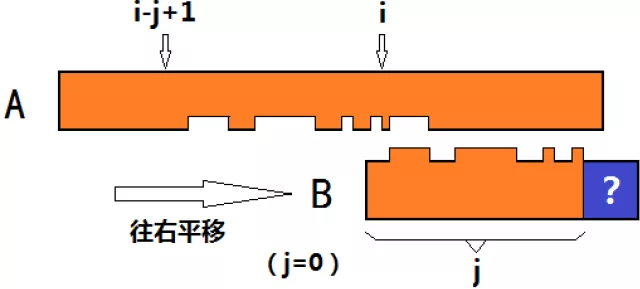
现在,就是用到了KMP算法的核心:它对这一情况的处理方式是减少j,就相当于将子串向右平移。
平移的目的是为了让“A[i-j+1~i]与B[1~j]均匹配”这个条件重新满足。
在上图中,j一直减小到了0,因为向右平移的过程中,始终不能让这个条件满足(最右边"?"部分已经越界)
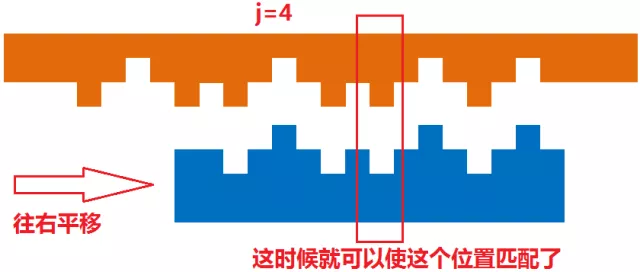
但有时候,将j减少一点点之后,是可以重新满足条件的,例如:
那么我们将j从7减小到4时,有:
这样就可以完全匹配啦!但是后面还有没有匹配的机会我们就不管了,至少我们已经保证A[4~7]和B[1~4]完全匹配上了。
现在考虑一个问题:我们每次把j减小1(一位一位地平移B字符串),这样太慢了,我们在这里预处理一个next[]数组,表示当j匹配不下去的时候,我们可以把j减少到next[j],继续尝试匹配。
预处理过程:让j自己和自己匹配一下,一旦匹配发现B[k-m+1~k] 和 B[1~m] 匹配,则说明在A与B匹配过程中,j等于k匹配不下去时,j可以尝试减小到m。
过程如下:
/**************************************///靓丽的分界线
一些代码:
/*核心内容*/
for (int i = 1, j = 0; i <= n; i++) { while (j&&B[j + 1] != A[i]) j = next[j]; if (B[j + 1] == A[i]) j++; if (j == m) { printf("%d\n", i - j + 1);//输出找到的"B字串在 A中位置" //如果要求的是出现次数,这里也有可能是ans++什么的 j = next[j];//让循环进行下去 } } for (int i = 2, j = 0; i <= m; i++)/*预处理next[]数组*/ {//j在每次循环开始都表示next[i]的值,同时也表示需要比较的下一个位置 while (j&&B[j + 1] != B[i]) j = next[j]; if (B[j + 1] == B[i]) j++; next[i] = j; }
经典例题:Blue jeans(POJ 3080)
给定m个串,求字典序最小的公共子串。找一个串,使得这个串是所有串的子串,并且字典序最小。
m≤10,每个串的长度≤60.
解题思路:一个串,如果是所有串的子串,那么肯定是第一个串的子串。
枚举所有子串,复杂度为60*60。
验证其它串是否包含这个子串,复杂度为10*60。
每次更新答案即可。
时间复杂度为:O(603×10)
经典例题:Seek the Name,Seek the Fame(POJ 2752)
给定一个字符串S,求所有既是S的前缀又是S的后缀的子串,从小到大输出这些串的长度。
|S|<=500000。
N为字符串S的长度。
解题思路:
回到KMP算法,我们令P[j]表示找最大的数x,使得B中位置是1~x的字符与j-x+1~j的字符完全相同,也就是上面讲的KMP算法中的next[]。
考虑P[|S|]的意义,也就是最大的前缀等于后缀的长度(不包括其本身)。
那P[P[|S|]]就是次大的。
因此所有P[P[…P[|S|]]]就是答案了,一直这样递归下去就可以找到答案。
或者用Hash来做,这样更容易想到也比较方便,但效率没有KMP高。