数论基础：斐波那契数列全讲

在烧脑之前的骚话

我仿佛在逗你玩。

Fibonacci数列

题目描述 Description
斐波纳契数列是这样的数列：
f1 = 1
f2 = 1
f3 = 2
f4 = 3
…
fn = fn-1 + fn-2
输入一个整数n
求fn

输入描述 Input Description
一个整数n, n<= 40

输出描述 Output Description
一个整数fn

数据范围及提示 Data Size & Hint
n<=10^16

样例输入 Sample Input	样例输出 Sample Output
3	2

时间限制: 1 s
空间限制: 64000 KB

初步构想——朴素递归法

写这道题最简短的代码就是递归。

#include
#include
using namespace std;
#define maxm 1001
int n;

int f(int x){
	if(x==1||x==2) return 1;
	return f(x-1)+f(x-2);
}

int main(){
	std::ios::sync_with_stdio(false);
	cin>>n;
	cout<<f(n);
	return 0;
}

不到二十行就可以敷衍的代码，每一次求x得值时就询问f(x-1)+f(x-2); 最后问道递归的x 为1，然后逐级return 回来。
然而递归法的缺点也是很大，那就是你每一次询问到1，n个数时的复杂度就是O(N),但是传递 到1之后还要回归 ，又是O(N)的复杂度。这一下就是O(2N)，因此，通常在递归写法下使用下一个小工具可以稍微优化时间复杂度。

二次思考——记忆化搜索

记忆化搜索在DP中是初学者常用的技巧，我们创建一个表，每一次递归出结果都把他记录在这个表上，下一次使用递归的时候，只需要在递归过程中额外询问一次表中是否有直接的结果，如果有，那就不需要继续递归了，直接使用表中数据，具体代码只是在原来的基础上改一下。

#include
#include
#include
using namespace std;
#define maxm 1001
int num[maxm],n;

int main(){
	std::ios::sync_with_stdio(false);
	cin>>n;
	
	if(n==1||n==2){cout<<"1";return 0;}
	num[1]=1;num[2]=1;
	for(int i=3;i<=n;i++)
		num[i]=num[i-1]+num[i-2];
	
	cout<<num[n];
	return 0;
}

代码似乎长了一点，但是也能在20行以内搞定。

终极写法——递归变递推

上一种写法看起来很好，但是如果我每次只查询一次，或者每一次故意就是查一些新的元素，让你非递过去归回来不可 （说实话很多题目的样例都会这样水你，然后测试数据都很恶心）
这样，我们的记忆化搜索似乎也没有优化多少。
所以，教练们一般教我们使用递推，递推不仅可以记忆化，还去掉了递过去归回来 的过程，可以使时间复杂度达到真正的O(N)。
线性复杂度是很诱人的呢。
上个代码先：

#include
#include
#include
using namespace std;
#define maxm 1001
int num[maxm],n;

int main(){
	std::ios::sync_with_stdio(false);
	cin>>n;
	
	if(n==1||n==2){cout<<"1";return 0;}
	num[1]=1;num[2]=1;
	for(int i=3;i<=n;i++)
		num[i]=num[i-1]+num[i-2];
	
	cout<<num[n];
	return 0;
}

分分钟搞定的简单代码。。。。。。

然而你真的以为这样写就可以AC了？
你会说：线性都不能AC难道你还有小于线性？
(⊙o⊙)…

重要的事情说三遍

看数据规模！！！！！！

看数据规模！！！！！！

看数据规模！！！！！！

时间限制1秒哦[淫荡的笑声 ]

所以你不管怎么样递推，超时都是必然的。
当然写成递归更刺激，直接崩栈。。。。。。

怎么优化呢？
话说没有小于线性的时间复杂度我写这个博客是闲得蛋疼。。。。。。
这是我学完RMQ算法后的小话题了。。。。。。
一开始我也不是很相信会有logN级别的斐波那契优化，且听我细细道来

快速幂

首先，你在求2^n次方时是怎么求的？
初步想法是：

int a=1;
for(int i=1;i<=n;i++){a*=2;}

先想到暴力是一个好习惯。
但是N的复杂度还是太慢了，如果像刚刚斐波那契数列那道题一样的变态数据规模你又如何处理？
我们可以这样思考：

求2^n的话
我们可以试着先求两个2^(n/2) 次方，然后乘一乘就可以得到 2^n
我们利用这样的分治思想可以快速求得2^n ，那么显然递归可以胜任这种逐步缩小范围最后返回正确答案的写法。

如果你这么认为的话，你还是太天真。
我也曾被这句话骗了好久，仿佛是这么个道理，但是做起来却绝对不符合事实。如果你不妨试试求一个奇数次方的，就用这种 “快速幂法” ，写起来就会有点点像线段树了。
[淫荡的笑声 ]当然你要真的想知道线段树这个东西我也不拦你，呵呵让你无语线段树
当然牛老们可以，然而很麻烦。有的又会开始想二分递归之类的东西。

我们这里不进行递归求解，我们使用倍增递推法。

二进制是个好东西，懂二进制的童鞋应该知道这一点。
二进制的1等于1
二进制10等于2
二进制100等于4
同理：
1000=8
10000=16
100000=32
1000000=64
10000000=128
100000000=256
……
那么，150该怎么用二进制表示？
其实就是10010110，等价于二进制下的10000000+10000+100+10。
也就是十进制的128+16+4+2。
那么2¹⁵⁰=2¹²⁸*2¹⁶*2⁴*2²
而150的二进制中的1对应着第几位的实际数就是2的几次方
比如二进制下第五位的1对应的就是16，也就是指2的16次方中的16。
那么存在这样的快速幂：

int fpow(int a,int p){
	int ans=1;
	for(;p;p>>=1,a*=a)
		if(p&1) ans*=a;
	return ans;
}

这里使用的位运算，对于位运算不了解的同学看这儿：
位运算包学包会
这个for循环没有初始条件，只要p不为零就会不停的循环。只要发现当前位下存在1，那就乘以当前位置的实际数，而a对应的就是当前位置的a的实际数次方，所以直接乘以ans即可。最后循环结束答案就是你要求得幂。本做法的复杂度是logN

高等数学基础——矩阵运算

这里讲三则基本矩阵运算。
首先是矩阵加减法。直接按位相加或相减。
如图：
1 3
2 4
加上
1 2
3 4
其实就是
2 5
5 8
相减就是
0 1
-1 0
简单提供以下矩阵加法的AC代码

#include
#include
#include
using namespace std;

#define maxm 1001
int n,m,a;
int e[maxm][maxm],b[maxm][maxm];

int main(){
	std::ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>e[i][j];
		}
	}
	
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>b[i][j];
		}
	}
	
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cout<<b[i][j]+e[i][j]<<" ";
		}cout<<endl;
	}
	return 0;
}

这里还有一段相加的WA。。。。。。说实话不知道哪儿错了
大佬指教！！！
大佬指教！！！
过了8个测试点两个WA。。。。。。

#include
#include
#include
using namespace std;

#define maxm 1001
int n,m,a;
int e[maxm][maxm];

int main(){
	std::ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>e[i][j];
		}
	}
	
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a;
			cout<<e[i][j]+a<<" ";
		}cout<<endl;
	}
	return 0;
}

关键是矩阵乘法
我概括出以下几点：

1. 矩阵A乘以B的时候，必须要求A的列数=B的行数，否则无法进行乘法运算。因此矩阵乘法也不满足交换律。
2. 设A是XN的矩阵，B是NY的矩阵，用A的每一行乘以B的每一列，得到一个XY的矩阵。 对于某一行乘以某一列的运算，我们称之 为向量运算，即对应位置的每个数字相乘之后求和。
   写为公式就是：
   C[i,j] = Sigma(A[i,k] * B[k,j])

比如：
1 3
2 4
乘以
1 2
3 4
答案就是
10 14
14 20
说白了就是酱紫：

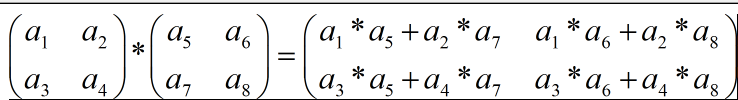
这里提供一下乘法的AC代码：

#include
#include
#include
using namespace std;
#define maxm 1001
int a[maxm][maxm],b[maxm][maxm],c[maxm][maxm],n1,m1,n2,m2;

int main(){
	std::ios::sync_with_stdio(false);
	cin>>n1>>m1;
	
	for(int i=1;i<=n1;i++){
		for(int j=1;j<=m1;j++){
			cin>>a[i][j];
		}
	}
	
	cin>>n2>>m2;
	for(int i=1;i<=n2;i++){
		for(int j=1;j<=m2;j++){
			cin>>b[i][j];
		}
	}
	
	for(int i=1;i<=n1;i++){
		for(int j=1;j<=m2;j++){
			for(int k=1;k<=n2;k++){	
				c[i][j]+=a[i][k]*b[k][j];
			}
		}
	}
	
	for(int i=1;i<=n1;i++){
		for(int j=1;j<=m2;j++){
			cout<<c[i][j]<<" ";
		}cout<<endl;
	}
	return 0;
}

矩阵快速幂

这里使用矩阵快速幂优化斐波那契数列
构造这样一个矩阵
0 1
1 1
然后把斐波那契数列的前两项也都构造矩阵：
也就是（长2宽1）
1 1
令这两个矩阵相乘，结果是
1 2
再乘以
0 1
1 1
这个矩阵。
结果是
2 3
我们发现，对于任意斐波那契数列中的数字a,b
乘以这个矩阵后都有b,a+b。
那么就满足了斐波那契数列的构造。
我们乘以1个这样的矩阵，那么结果矩阵的第一个数字就是第1个斐波那契数。
我们乘以n个这样的矩阵，那么结果矩阵的第一个数字就是第n个斐波那契数。
这样，我们就可以把斐波那契数列转换为[1,1]乘以n个[0111矩阵]的问题
既然这样，就可以直接使用快速幂解决。
但是原本快速幂的乘号都要换成矩阵乘法。
代码写起来会稍稍复杂。

#include
#include
#include
#include
using namespace std;
int n,k,ans[2][3],a[3][3],t[3][3];

void fpow(int p){
	for(;p;p>>=1){
		if(p&1){
			memset(t,0,sizeof(t));
			for(int i=1;i<=2;i++){
				for(int j=1;j<=2;j++){
					t[1][i]+=ans[1][j]*a[j][i];
				}
			}
			for(int i=1;i<=2;i++){
				ans[1][i]=t[1][i];
			}
		}
		
		memset(t,0,sizeof(t));
		for(int i=1;i<=2;i++){
			for(int j=1;j<=2;j++){
				for(int k=1;k<=2;k++){
					t[i][j]+=a[i][k]*a[k][j];
				}
			}
		}
		
		for(int i=1;i<=2;i++){
			for(int j=1;j<=2;j++){
				a[i][j]=t[i][j]; 
			}
		}
	}	
	return;
}

void init(){
	ans[1][1]=1;ans[1][2]=1;
	a[1][1]=0;a[1][2]=1;
	a[2][1]=1;a[2][2]=1;
	return;
}

int main(){
	std::ios::sync_with_stdio(false);
	init();
	cin>>k;
	fpow(k-1);
	
	cout<<ans[1][1];
	return 0;
}

以上求斐波那契数列的代码复杂度为logN，可以轻轻松松AC顶部例题而不超时。