AC自动机详解

请务必保证已经学会了kmp和Trie，如果对kmp和Trie还不熟练，请先阅读这两篇博客进行学习：

kmp ：http://blog.csdn.net/hao_zong_yin/article/details/75165028

Trie： http://blog.csdn.net/hao_zong_yin/article/details/77127070

参考资料

1.http://blog.csdn.net/niushuai666/article/details/7002823

一开始看不懂他写的什么意思，但翻了翻其他博客对ac自动机有了一定了解之后发现他写的真心不错

2.http://blog.csdn.net/mobius_strip/article/details/22549517

极力推荐，我的模板差不多就是受了他的启发

3.http://blog.csdn.net/creatorx/article/details/71100840

这篇博客对初学者很友好，推荐初学时先按照他的思路走一遍，再去看前两篇博客，有助于加深理解

4.蓝书

刘汝佳的模板应该是效率最高的模板了，采用了Trie图优化和last数组优化，但是last数组比较难懂，所以我只参考了他的trie图优化，另外刘汝佳的模板和这个博主的差不多：http://blog.csdn.net/u012350533/article/details/18097301

5.kuangbin的总结http://www.cnblogs.com/kuangbin/p/3164106.html

kuangbin总结的题目一向很好

看了三天AC自动机，总算把模板外加HDU2222弄出来了，这里以HDU2222为例写一下总结：

一。什么是AC自动机

AC自动机解决的是多个模式串匹配一个文本串的问题， 比如HDU2222，给你多个模式串，问你有多少个模式串在文本串中出现过

假设有n个模式串，文本串长度为len，并且只考虑查询时的复杂度

如果我们用kmp解决这个问题，那么就要用所有模式串与文本串进行匹配，复杂度为O（len * n）。

但是ac自动机却可以在线性时间内解决这个问题，复杂度为O（len）。

二。怎样实现AC自动机

实现ac自动机需要3步：

1.建Trie

2.构造fail指针

3.查询

在具体分析之前先说说大体流程：

众所周知kmp的模式串在失配时会根据一个预先构造好的数组进行跳转，从而不用逐个比较，提高了效率； ac自动机的思想和kmp差不多，也是在失配时进行跳转，不过ac自动机不只是在一个模式串中进行跳转，还能在不同模式串之间进行跳转。

kmp在进行跳转时是遵循的是最长相同前后缀的原则； ac自动机在跳转的时候也是遵循最长相同前后缀的原则，不过后缀是当前字符串的后缀，前缀是跳转后的模式串的前缀

这就用到了Trie，想象一下，你已经根据所有模式串构造出了一棵字典树，现在你需要拿着文本串从root节点开始查找。当你发现文本串的一部分和当前的模式串刚好匹配时，那么就说明当前的模式串在文本串中出现过，然后继续拿着剩下的文本串进行查找；当你发现文本串不能继续匹配时，一般思想是重新从root开始查找，但是ac自动机是根据失配节点的fail指针跳转到另一个节点，然后从这个节点继续查找，如此往复直到查找结束。

fail指针的跳转规则：保证【当前字符串后缀】与【跳转后模式串的前缀】【相同】且【长度最长】（长度最长是为了方便用bfs构造fail指针），比如有三个模式串abcd、bcd、cd，现在要构造模式串abcd中d的失配指针，当前字符串为abc（不包括d），后缀是bc和c，能够匹配模式串bcd和cd的前缀，根据长度最长原则，我们选择另后缀bc匹配模式串bcd的前缀bc，即另4号节点的fail指针指向7号节点。同理对于7号节点，它代表的字符串bc的后缀c只能匹配模式串cd的前缀c，所以7号节点的fail指针指向9号节点，9号节点代表的字符串c没有可以匹配的模式串前缀，所以指向root（0），流程图如下：

仔细理解一下你会发现这个过程和kmp非常类似，说白了就是在上面三条链上用kmp啪啪地跳。

大体流程说完了再来看看具体实现，这里用到了HDU2222的例子：

假设有5个模式串she he say shr her和一个文本串yasherhs，要求在文本串中查找有多少个模式串出现过（she he her3个）

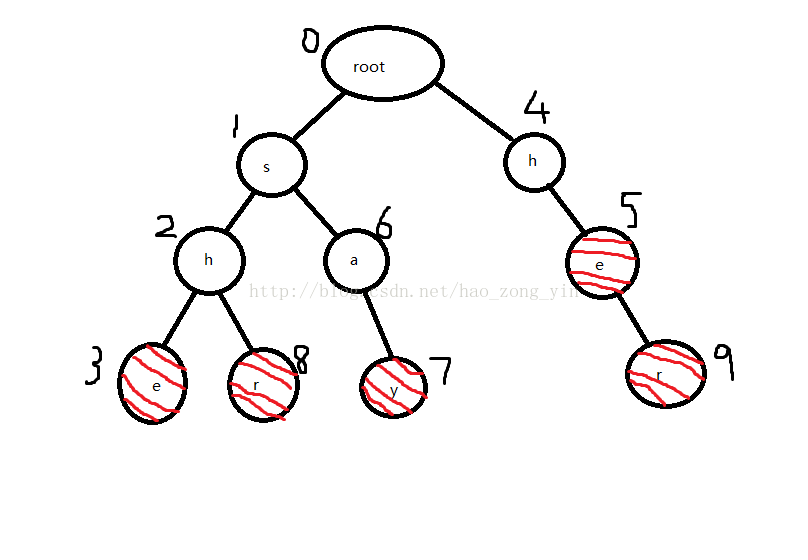
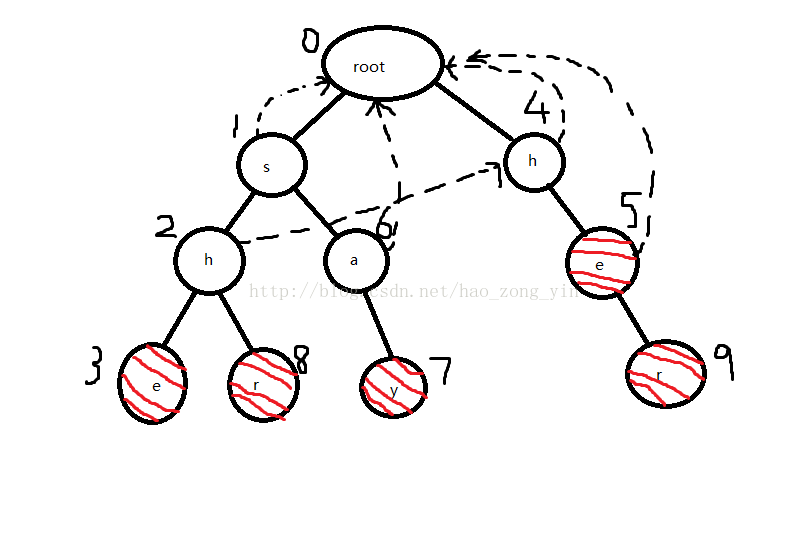
1.建Trie

2.构造fail指针

fail指针在跳转后的深度一定小于跳转前的深度，所以我们用bfs求解。

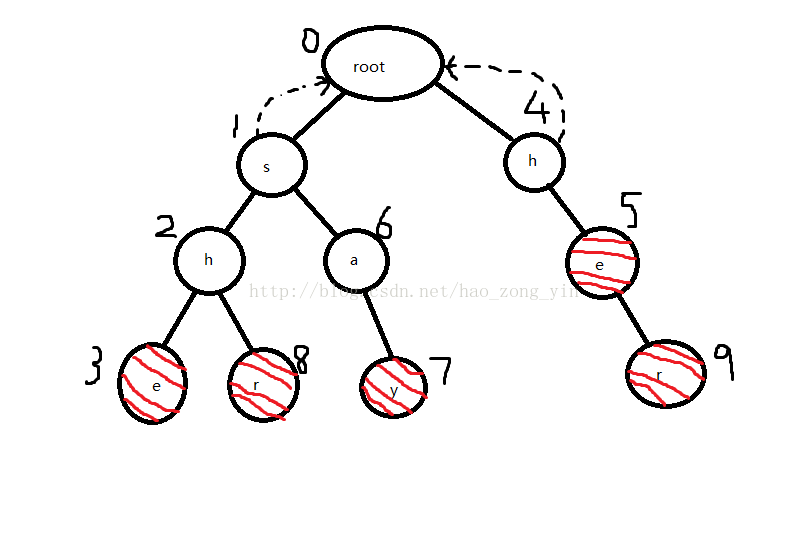
创建一个队列，把root的孩子s和h入队，然后把他们的fail指针指向root

当前队列：sh

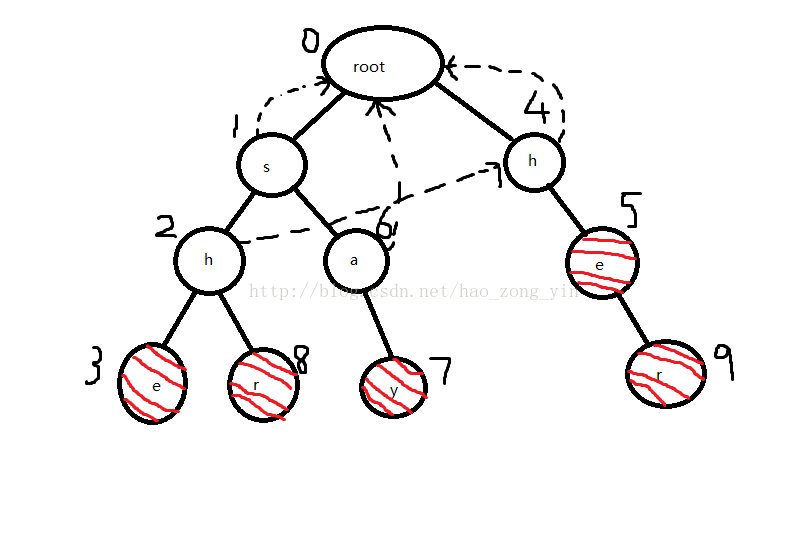
然后s出队，他的孩子h（2）和a（6）入队，对于h（2），先找到s的fail指针指向的节点root，发现root的孩子中有h，故把2号节点的fail指针指向4号节点，对于a（6），同样先找到s的fail指针指向的节点root，发现root的孩子中没有a，故直接把2的fail指针指向0。

为什么要先找s的fail指针指向的节点，并进行判断呢？因为根据bfs的顺序，s的fail指针一定已经构造好了，【s节点代表的字符串的后缀】一定与【s的fail指针指向的节点代表的字符串的前缀】匹配，所以要找h、a的fail指针指向的节点，只需要看看s的fail指针指向的root节点的孩子中有没有h、a即可，有的话指向这个节点（比如2指向4），没有的话指向0（比如6指向0）

当前队列：hha

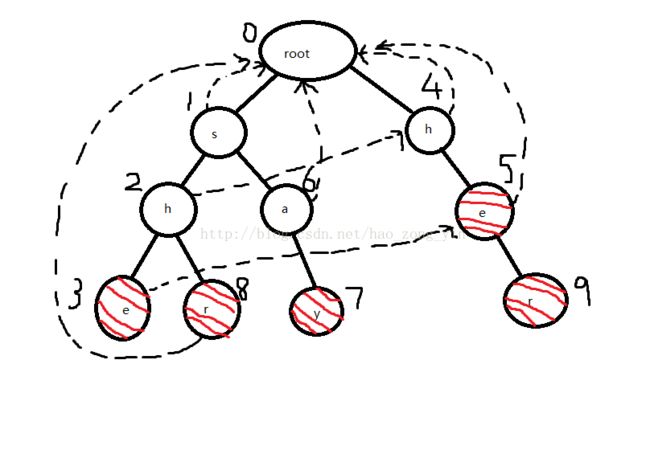
然后h（4）出队，他的孩子e（5）入队，并且把5的fail指针指向0。

当前队列：hae

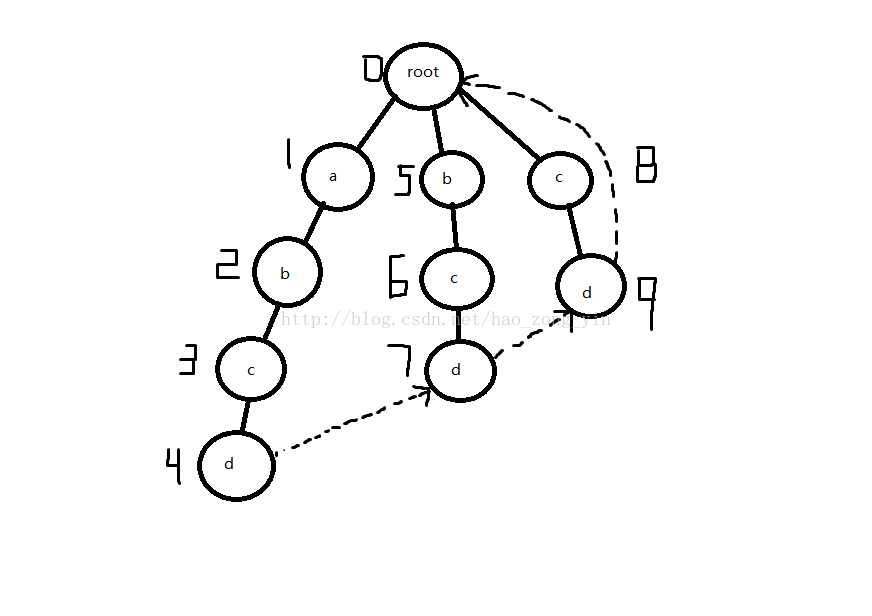
然后h（2）出队，他的孩子e（3）、r（8）入队，根据规则e（5）要找2的fail指针指向的节点4，发现4的孩子5也是e，所以3指向5，同理8指向0

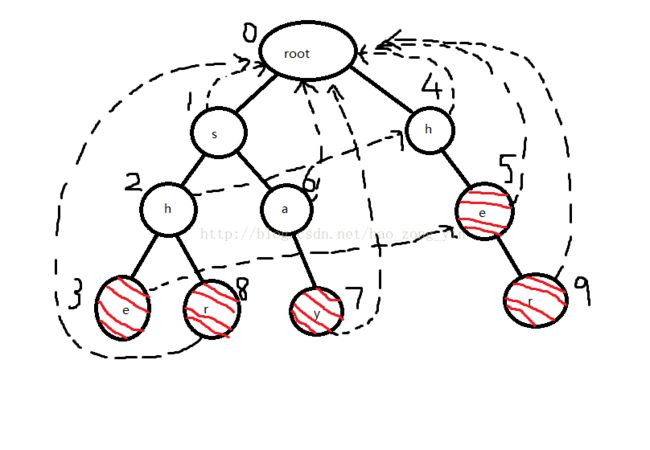
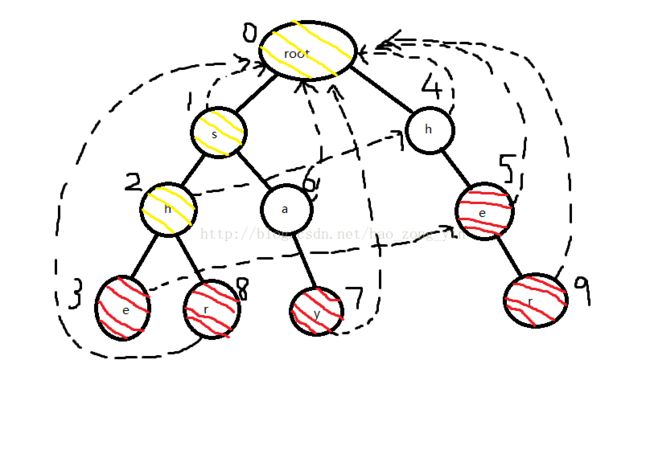
之后7和9都会指向0，就不多说明了，最终fail指针图：

3.查询

查询过程最终要的就是不重不漏，为了不重，我们统计完一个模式串节点后就把这个节点的值设为0防止再次统计，为了不漏，我们每经过一个节点就要走一遍他的fail路径，统计路径上的所有模式串节点（就是那些红色的点。。。）

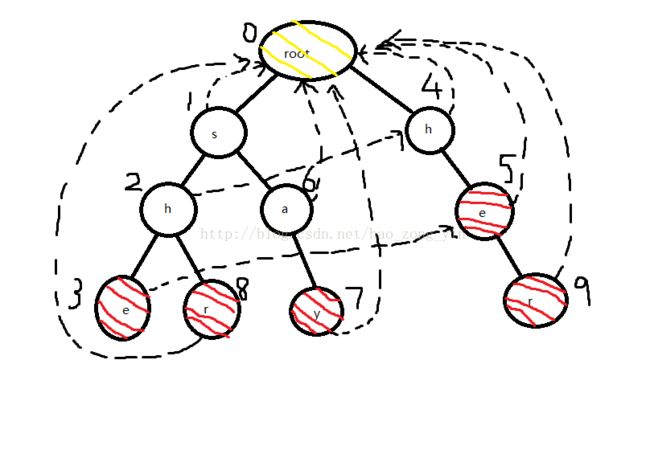
下面就来查询一下yasherhs：

对于前两个ya，在Trie中走不动，还是停留在root（黄色节点仅仅是为了好看，没有实际意义）

当前文本串：sherhs

对于s，可以走到1，然后遍历一遍1的fail路线，并没有红色节点可以统计，对于2也是

当前文本串：erhs

对于e（3）就不同了，他的fail路径上有3 5是红色的，所以ans会加2（把3 5清空防止重复统计），并且下一个点应该从5开始

当前文本串：rhs

然后走到r（9）,他的fail路径中9是红色的，统计一次，ans加1，并且下一个点从root开始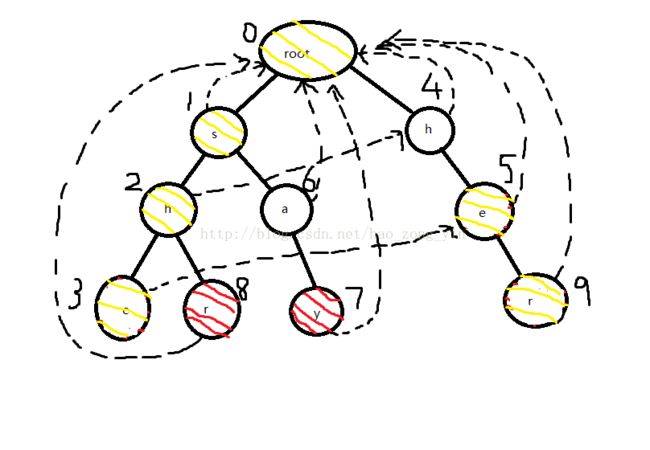

对于剩下的hs，什么也查不到，我就不画图了，最终结果是ans=3；

三。Trie图优化AC自动机

Trie图优化实在构建fail指针补充失配边从而优化查找过程，这个优化非常方便，而且比起不优化的过程更容易理解，具体过程就是在失配时直接把更改Trie，把失配点和他的fail指针指向的点连接起来，这样在查找时完全不用考虑fail指针直接一路走到底即可，具体参考模板的注释。

四。模板

struct AC {
    int ans, total, val[MAXN], fail[MAXN];//ans保存题目解，total分配新节点，val存节点值，fail是失配指针
    int child[MAXN][SIZE];

    void init() {//使用ac自动机前务必初始化
        ans = 0; total = 1;
        memset(val, 0, sizeof(val));
        memset(fail, 0, sizeof(fail));
        memset(child[0], 0, sizeof(child[0]));
    }
    void Insert(const char *P) {//构造字典树
        int root = 0;
        for (int i = 0; P[i]; i++) {
            if (!child[root][P[i] - 'a']) {
                memset(child[total], 0, sizeof(child[total]));
                child[root][P[i] - 'a'] = total++;
            }
            root = child[root][P[i] - 'a'];
        }
        val[root]++;
    }
    void Getfail() {//bfs构造fail指针
        queue q;
        for (int i = 0; i < SIZE; i++) {//首先把root的所有儿子的fail指针都指向root
            if (child[0][i]) q.push(child[0][i]);//因为节点的fail指针默认为root所以就简写了
        }
        while (!q.empty()) {
            int root = q.front(); q.pop();
            for (int i = 0; i < SIZE; i++) {
                int u = child[root][i];
                if (!u) { child[root][i] = child[fail[root]][i]; continue; }//Trie图优化，建立失配边
                q.push(u);
                int v = fail[root];
                while (v && !child[v][i]) v = fail[v];//构造fail指针的关键，推荐画图辅助理解
                fail[u] = child[v][i];
            }
        }
    }
    void Search(const char *T) {
        Getfail();
        int root = 0, temp;
        for (int i = 0; T[i]; i++) {
            temp = root = child[root][T[i] - 'a'];//因为经过了Trie图优化，所以这里只要沿着root走就可以
            while (temp && val[temp]) {//遍历fail路径，防止遗漏
                ans += val[temp];
                val[temp] = 0;//防止重复统计，根据题目而定
                temp = fail[temp];
            }
        }
    }
}ac;