【数据结构】线段树的扩展与应用

线段树是一种非常基础的数据结构，但有的时候仅仅是普通的线段树无法满足需求，那么我们就要对其进行一些扩展。

Chapter1：标记永久化

实现

普通的线段树通过懒标记(Lazy Tag)以$O(nlogn)$的复杂度实现对序列的区间修改和查询。但有些时候想要向下$push\_down$标记和向上$push\_up$维护并不是那么方便，这个时候就需要用到标记永久化了。

标记永久化的思想和懒标记相反：既然我不能方便地下传标记和合并答案，那么干脆就直接更新， 只有当这个区间整个被修改的时候才打标记。（其实与之前的区间开平方的思想有些类似，只要一整个区间都变为1了，我就打个标记表示不需要处理）

以区间加、区间求和为例，如果我当前访问的线段树节点所代表的区间包含了我要修改的区间，那么很明显修改完后的贡献是可以直接算出来的，也就是修改的区间长乘上增加的值，那么我们就可以直接更新当前点的答案。

那么如果我们朴素地更新，那么一次修改肯定会变为$nlogn$的，因为我们会一直更新到叶子节点。那么这个时候我们还是需要打上一个标记，只不过这个标记只打在整个区间都被修改的节点上，而且不需要下传。

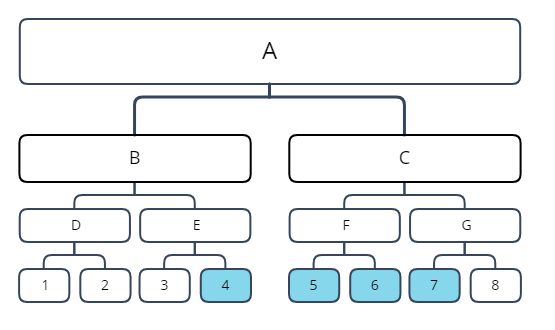
举个栗子，对于一个元素个数为8的序列，假设我们要给图中染色的节点加上$k$，那么我们修改的过程应该是这样的：

对于根节点$A$，它包含了一整个修改区间（长度为$4$），那么我们将它的答案加上$4k$，但由于它不是被完整修改的，所以我们不能打标记，接着向下递归。

对于$B$节点，他包含了$1$个待修改的元素，那么它的值就应该加上$k$，$E$节点同理。

然后到了底层叶子结点$4$，首先它的答案也应该加上$4$，然后由于它被完整覆盖了，所以需要打上一个值为$k$的标记。

然后来到$C$节点，它包含$3$个待修节点，答案加上$3k$，然后来到$F$。

$F$答案加上$2k$，但此时我们发现它被完整覆盖了，于是我们打上$2k$的标记，然后不再向下递归。

对于$G$，答案加上$k$，然后在$7$节点答案加$k$，打上标记。

于是我们可以给出修改的代码：

//s为节点代表的的区间和,tag是节点的标记
void update(int p, int l, int r, int ul, int ur, ll k){
    s[p] += (ur-ul+1)*k;		//直接统计答案
    if(l == ul && r == ur){		//被完全覆盖,打标记
        tag[p] += k;
        return;
    }
    //从上述分析可以看出,与普通线段树不同,在标记永久化的时候,由于需要判断节点是否被完全覆盖
    //我们需要同时二分节点代表的区间和询问的区间,这样才可以保证询问区间包含在当前区间内,才可以直接统计答案
    if(ul > mid) update(rc(p), mid+1, r, ul, ur, k);
    else if(ur <= mid) update(lc(p), l, mid, ul, ur, k);
    else update(lc(p), l, mid, ul, mid, k), update(rc(p), mid+1, r, mid+1, ur, k);
}

接着考虑如何查询答案。

其实只要理解了我们在修改时打标记的意义，查询就变得非常简单了。由于我们的标记表示的是对整段区间进行的修改，那么只要这个节点包含查询区间，那么它的标记就会对查询结果产生影响。于是我们只要在查询的时候累加经过的节点上的标记，当整个节点都是查询区间的时候，我们就返回这个节点自身的答案加上累加的标记对区间的影响。

那么查询的代码也就十分简单：

ll query(int p, int l, int r, int ul, int ur, ll sum){	//sum是路径上累加的标记和
    if(l == ul && r == ur) return s[p]+sum*(r-l+1);
    //和修改一样，也要二分查询区间
    if(ul > mid) return query(rc(p), mid+1, r, ul, ur, sum+tag[p]);
    else if(ur <= mid) return query(lc(p), l, mid, ul, ur, sum+tag[p]);
    else return query(lc(p), l, mid, ul, mid, sum+tag[p])+query(rc(p), mid+1, r, mid+1, ur, sum+tag[p]);
}

完整代码可以参考我的提交记录：线段树1

小结

标记永久化相对标记下传没那么好理解，并且局限性较强，比如不能像传统线段树那样维护如区间最大子段和这种相对复杂、不能直接统计答案的信息。但是在一些特定的场合，标记下传会显得非常不方便，那么就需要标记永久化。

---

Chapter2：二维线段树（树套树 Tree Tao Tree）

题意：

维护一个矩阵中的信息：支持修改子矩阵，查询子矩阵和（或最大/最小值）。

实现

现在一维序列上的操作被扔到了二维平面上，那么一个最直接的想法就是通过一些方法强行转换成一维操作（比如在树上可以利用$dfs$序）。

我们可以把两维分开考虑，如果我们把每一列看成一个点，那么我们就可以把整个矩阵拍扁，看成一个序列，就可以进行常规的线段树操作了。

那么每一列内的信息怎么维护呢？显然对每一列开一个内层线段树就完了。

所以我们使用树套树，外层线段树维护行，内层线段树维护列。这时候我们会发现外层线段树区间修改的时候标记没法下传，那就要用到上文介绍的标记永久化了。

代码

P3437 TET-Tetris 3D

只要对标记永久化比较熟练，代码总体就非常好理解。

#include 
#include 
#define MAX 2050
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
using namespace std;

template<typename T>
inline void read(T &n){
    n = 0;
    T f = 1;
    char c = getchar();
    while(!isdigit(c) && c != '-') c = getchar();
    if(c == '-') f = -1, c = getchar();
    while(isdigit(c)) n = n*10+c-'0', c = getchar();
    n *= f;
}

template<typename T>
inline void write(T n){
    if(n < 0) putchar('-'), n = -n;
    if(n > 9) write(n/10);
    putchar(n%10+'0');
}

int n, m, q;

inline int max(int x, int y){
    return x>y?x:y;
}

struct segy{
    int mx[MAX], tag[MAX];

    void update(int p, int l, int r, int ul, int ur, int k){
        mx[p] = max(mx[p], k);
        if(l == ul && r == ur){
            tag[p] = max(tag[p], k);
            return;
        }
        int mid = (l+r)>>1;
        if(ur <= mid) update(lc(p), l, mid, ul, ur, k);
        else if(ul > mid) update(rc(p), mid+1, r, ul, ur, k);
        else update(lc(p), l, mid, ul, mid, k), update(rc(p), mid+1, r, mid+1, ur, k);
    }
    int query(int p, int l, int r, int ul, int ur){
        if(l == ul && r == ur) return mx[p];
        int res = tag[p], mid = (l+r)>>1;
        if(ur <= mid) res = max(res, query(lc(p), l, mid, ul, ur));
        else if(ul > mid) res = max(res, query(rc(p), mid+1, r, ul, ur));
        else res = max(res, max(query(lc(p), l, mid, ul, mid), query(rc(p), mid+1, r, mid+1, ur)));
        return res;
    }
};
struct segx{
    segy mx[MAX], tag[MAX];

    void update(int p, int l, int r, int ul, int ur, int yl, int yr, int k){
        mx[p].update(1, 1, m, yl, yr, k);
        if(l == ul && r == ur){
            tag[p].update(1, 1, m, yl, yr, k);
            return;
        }
        int mid = (l+r)>>1;
        if(ur <= mid) update(lc(p), l, mid, ul, ur, yl, yr, k);
        else if(ul > mid) update(rc(p), mid+1, r, ul, ur, yl, yr, k);
        else update(lc(p), l, mid, ul, mid, yl, yr, k), update(rc(p), mid+1, r, mid+1, ur, yl, yr, k);
    }

    int query(int p, int l, int r, int ul, int ur, int yl, int yr){
        if(l == ul && r == ur) return mx[p].query(1, 1, m, yl, yr);
        int res = tag[p].query(1, 1, m, yl, yr), mid = (l+r)>>1;
        if(ur <= mid) res = max(res, query(lc(p), l, mid, ul, ur, yl, yr));
        else if(ul > mid) res = max(res, query(rc(p), mid+1, r, ul, ur, yl, yr));
        else{
            res = max(res, query(lc(p), l, mid, ul, mid, yl, yr));
            res = max(res, query(rc(p), mid+1, r, mid+1, ur, yl, yr));
        }
        return res;
    }
}a;

int main()
{
    read(n), read(m), read(q);
    int x, y, d, s, h;
    while(q--){
        read(d), read(s), read(h), read(x), read(y);
        x++, y++;
        int mx = a.query(1, 1, n, x, x+d-1, y, y+s-1);
        a.update(1, 1, n, x, x+d-1, y, y+s-1, mx+h);
    }
    write(a.query(1, 1, n, 1, n, 1, m));

    return 0;
}

Chapter3：线段树合并

在某些情况下，我们的权值线段树需要合并（一般区间树是不进行合并的）。那么最简单的方法就是启发式合并，复杂度$O(nlo{g}^{2}n)$，但由于线段树的一些优美的性质，我们可以把线段树的合并在$O(nlogn)$复杂度内完成。

实现

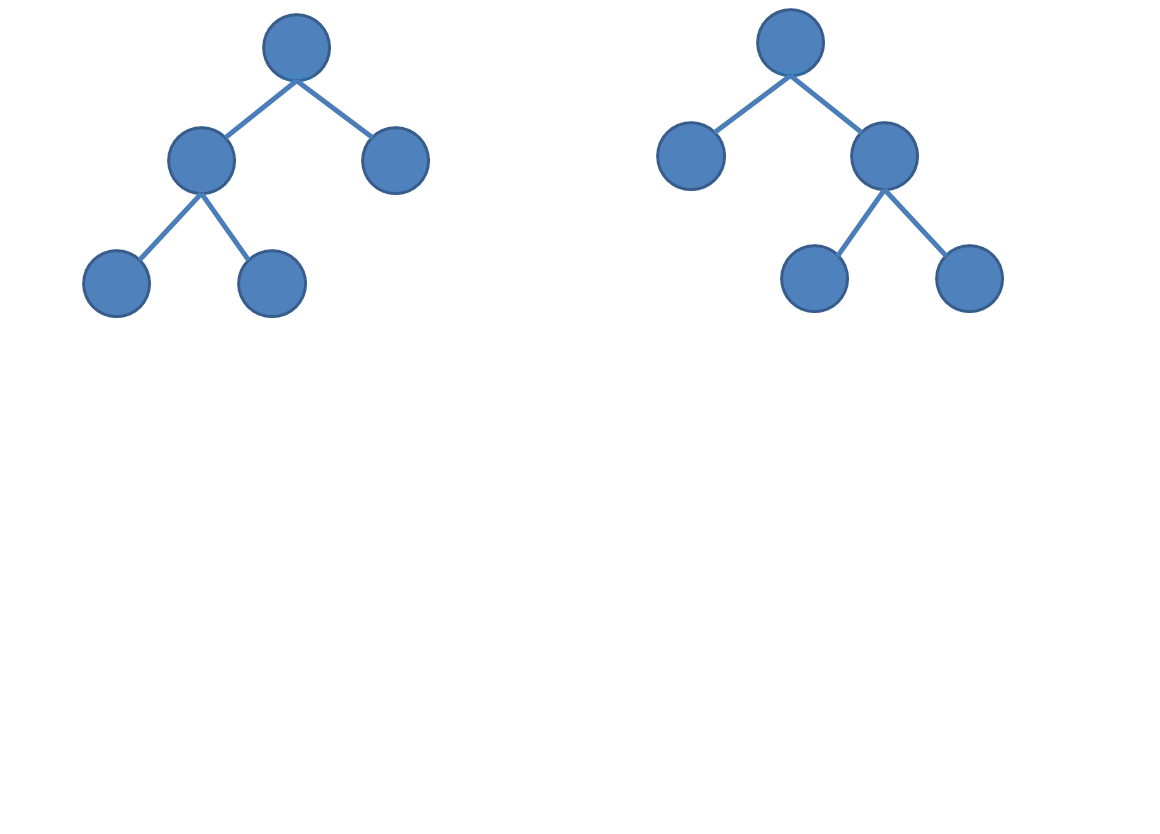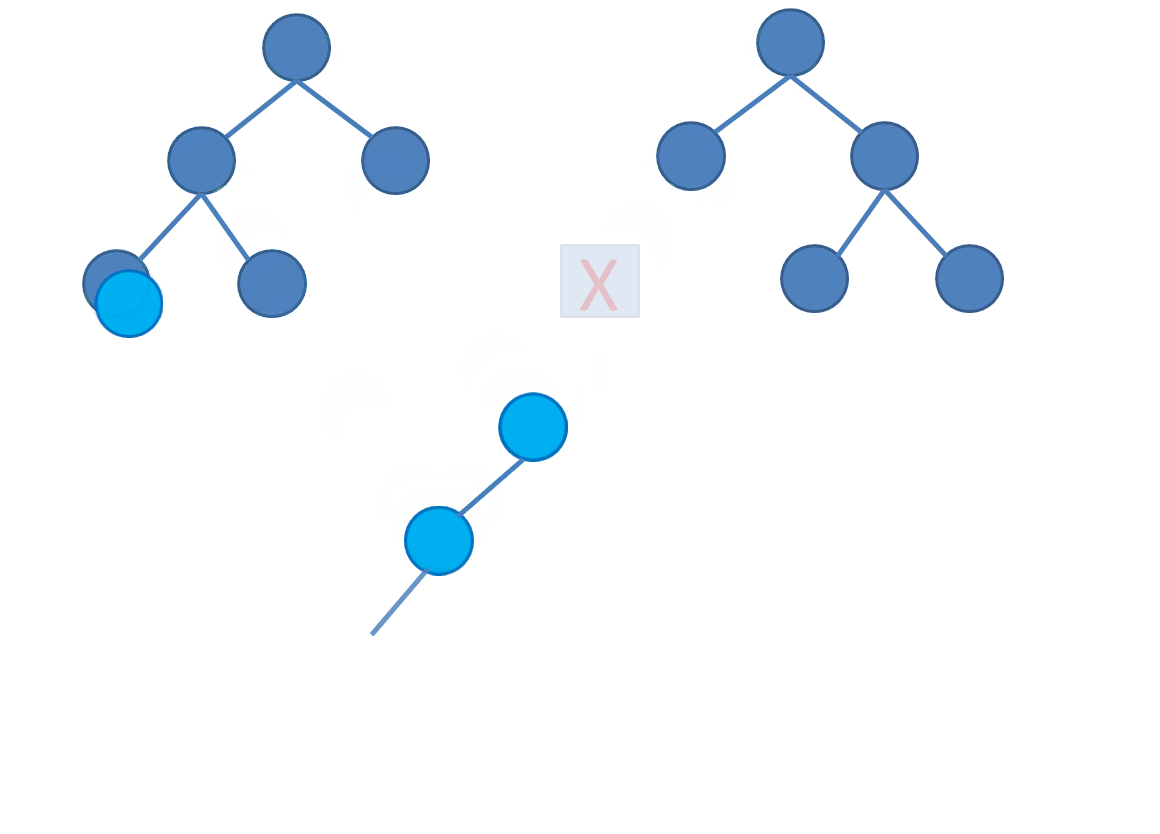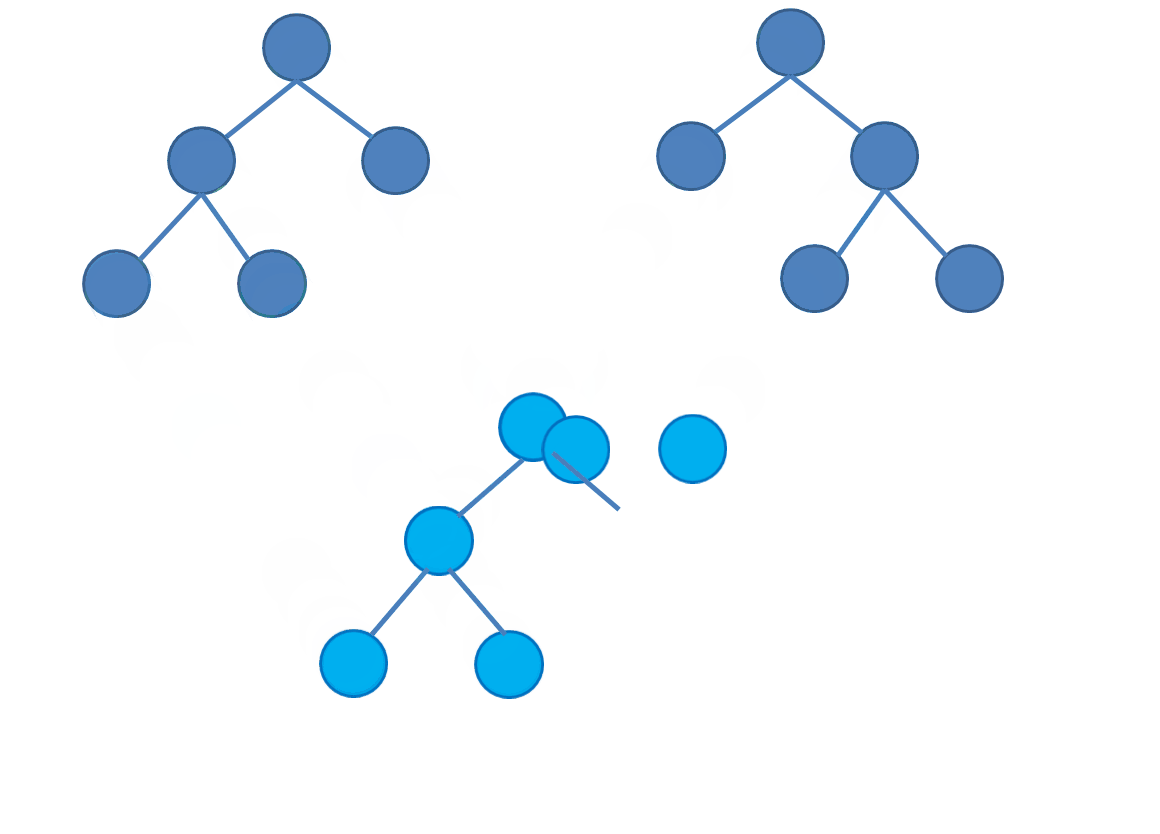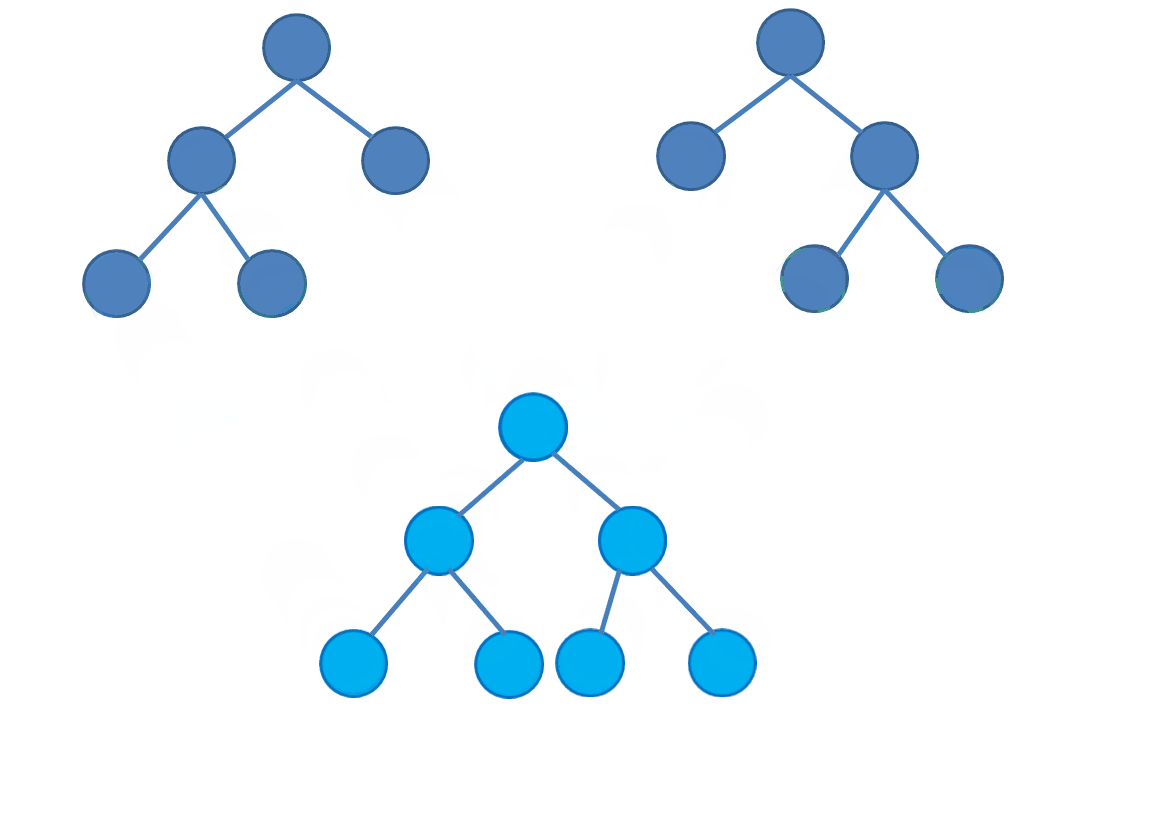
先上图感受一下：

其实线段树合并非常简单，只要在普通的线段树上二分的时候进行一些判断就可以了。

具体操作（可以结合上图感性理解）：

1. 如果当前节点和另一棵树上对应位置的节点都有左儿子，那么递归到左子树合并。
2. 如果当前节点和对应位置节点只有一个有左儿子，那么直接把唯一的左儿子作为合并后这个位置节点的左儿子。（直接拉过来接上去）
3. 如果都没有左儿子，就不进行合并。
4. 右儿子同理。

是不是非常简单啊！！

代码

线段树合并有两种实现方式，一种是动态开点，优点是可以不影响原线段树的形态，但是空间复杂度较高；还有一种是直接把另一颗线段树合并到当前线段树上，这样会破坏原线段树的结构，但是空间复杂度较低（适合询问离线）。

下面的实现节选自P4556 雨天的尾巴 的代码，本题可以离线询问，所以使用第二种方式。

void merge(int x, int y, int l, int r){		//线段树合并
    if(l == r){
        s[x] += s[y];
        return;
    }
    if(lc[x] && lc[y]) merge(lc[x], lc[y], l, mid);		//如果都有左孩子，递归合并
    else if(lc[y]) lc[x] = lc[y];		//否则直接接上去
    if(rc[x] && rc[y]) merge(rc[x], rc[y], mid+1, r);		//右儿子同理
    else if(rc[y]) rc[x] = rc[y];
    push_up(x);
}

完结撒花

线段树虽然很基础，但是还是有很多巧妙的扩展和应用，还有猫树、zkw各种变种~~（挖坑警告！）~~。