acm--manacher（马拉车算法）（HDU 3294）

HDU3294(求最长回文)

Girls’ research

Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 3075 Accepted Submission(s): 1177

Problem Description
One day, sailormoon girls are so delighted that they intend to research about palindromic strings. Operation contains two steps:
First step: girls will write a long string (only contains lower case) on the paper. For example, “abcde”, but ‘a’ inside is not the real ‘a’, that means if we define the ‘b’ is the real ‘a’, then we can infer that ‘c’ is the real ‘b’, ‘d’ is the real ‘c’ ……, ‘a’ is the real ‘z’. According to this, string “abcde” changes to “bcdef”.
Second step: girls will find out the longest palindromic string in the given string, the length of palindromic string must be equal or more than 2.

Input
Input contains multiple cases.
Each case contains two parts, a character and a string, they are separated by one space, the character representing the real ‘a’ is and the length of the string will not exceed 200000.All input must be lowercase.
If the length of string is len, it is marked from 0 to len-1.

Output
Please execute the operation following the two steps.
If you find one, output the start position and end position of palindromic string in a line, next line output the real palindromic string, or output “No solution!”.
If there are several answers available, please choose the string which first appears.

Sample Input

b babd
a abcd

Sample Output

0 2
aza
No solution!

普通方法解

遍历每个位置，判断是否能用某位置为中心形成回文。

不过回文可能是奇或者偶，比如qaq与qaaq都是回文。

/**
 * hdu3294
 * 法一：普通方法
 * 模拟着向两边扩散搜
 */

#include
#include
#include

using namespace std;
const int mmax = 200005;

int main()
{
    char c;
    char s[mmax];
    char result[mmax];

    while(scanf("%c", &c) == 1)
    {
        int t = c-'a';

        scanf("%s", s);
        memset(result, 0, sizeof(result));

        int len = strlen(s);
        int maxl = 0;
        int left,right;

        for(int i = 1; i < len; i++)
        {
            int l;
            //为奇数时
            for (l = 1; ; l++)
            {
                if(i+l > len-1 || i-l < 0)
                {
                    break;
                }
                if(s[i+l] != s[i-l])
                {
                    break;
                }
                if(l*2+1 > maxl)
                {
                    maxl = l*2+1;
                    left = i - l;
                    right = i + l;
                }
            }
            //为偶数时
            for(int l = 1; ; l++)
            {
                if(i+l-1 > len-1 || i-l < 0)
                {
                    break;
                }
                if(s[i+l-1] != s[i-l])
                {
                    break;
                }
                if(l*2 > maxl)
                {
                    maxl = l * 2;
                    left = i - l;
                    right = i + l - 1;
                }
            }
        }

        if(maxl == 0)
        {
            printf("No solution!\n");
        }
        else
        {
            printf("%d %d\n", left, right);
            for(int i = left; i <= right; i++)
            {
                if(s[i] - t >= 'a')
                    printf("%c", s[i]-t);
                else
                    printf("%c", s[i]-t+('z'-'a'+1));
            }
            printf("\n");
        }
        getchar();
    }

    return 0;
}

manacher算法

简介

这个马拉车算法Manacher‘s Algorithm是用来查找一个字符串的最长回文子串的线性方法，由一个叫Manacher的人在1975年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性，即复杂度变为O(n)。

1.我们先无论奇偶，把字符串变为奇数个，这样就不用分奇偶两种情况了。（如下所示）
qaq => #q#a#q#
qaaq => #q#a#a#q#
原因也很简单，即n*2+1一定是奇数

另外，大多数人选择在前面加一个标识用来判断边界，比如
qaq => *#q#a#q#

2.manacher充分利用了回文串的性质。比如一个回文（这里使用奇数回文，因为根据上一条可以知道偶回文可以转化为奇回文）

下标	0	1	2	3	4	5	6	7	8
字符	g	b	a	b	c	b	a	b	k

在遍历下标为6的字符时，普通的方法就看下标为5和下标为7所代表的字符是否相等，如果相等则判断4和8

而我们的manacher，在遍历下标为6的字符时，（此时最长串为”babcbab”，下标从1~7，中心为下表为4的’c’），由于下标6在1~7内，直接利用回文的对称性，下标6和下标2（2 = 4 * 2 - 6）关于4对称。于是直接判断第4位和第8位是否相等。

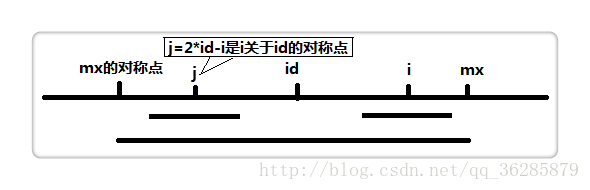
3.我们新增两个变量，大多数人取名为mx（对称中心的幅射范围，幅射半径）与id（对称中心），然后再创建一个p数组，用来存每个下标所对应的最长回文的半径。如下图（网上找的，侵删）：

下标i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
字符	*	#	g	#	b	#	a	#	b	#	c	#	b	#	a	#	b	#	k	#
p[i]	1	1	2	1	2	1	3	1	2	1	2	1	2	1	3	1	2	1	2	1

先判断i与mx的关系，
i < mx，则p[i] = min(p[2*id-i], mx - i);
i > mx, 则p[i] = 1;表示该点没有优化，还是老老实实按普通方法来。

然后和普通方法一样，只不过是从p[i]开始向两边扩展。

代码实现

/**
 * 法二：
 * 马拉车算法
 */

#include
#include
#include

using namespace std;

const int mmax = 200005;
char str1[mmax];
char str2[mmax*2];
int p[mmax*2];

int main()
{
    char s[5];

    int id, mx;
    int resi, resl;

    while(scanf("%s %s", s, str1) == 2)
    {
        int len = strlen(str1);
        memset(str2, '#', sizeof(str2));
        memset(p, 0, sizeof(p));
        mx = 0;
        id = 0;
        resi = 0;
        resl = 0;

        str2[0] = '*';
        for(int i = 0; i < len; i++)
        {
            str1[i] = (str1[i]-'a'-(s[0]-'a')+26)%26+'a';
            str2[i*2+2] = str1[i];
        }

        for(int i = 2; i < len*2+2; i++)
        {
            p[i] = i < mx? min(p[2*id-i], mx - i) : 1;

            while(str2[i + p[i]] == str2[i - p[i]])
                ++p[i];
            if(mx < i + p[i])
            {
                mx = i + p[i];
                id = i;
            }
            if(p[i]-1 > resl)
            {
                resl = p[i]-1;
                resi = i;
            }

        }

        if(resi < 2)
            printf("No solution!\n");
        else
        {
            printf("%d %d\n", (resi - resl - 1) / 2, (resi + resl + 1) / 2 - 2);
            for (int i = (resi - resl - 1) / 2; i < (resi + resl + 1) / 2 - 1; i++)
            {
                printf("%c", str1[i]);
            }
            printf("\n");
        }

    }


    return 0;
}

复杂度分析

只要在i < mx就可以进行优化，所以只进行扩展mx的复杂度，即O(mx)=O(2n)=O(n)，其中2n表示进行加’#’操作后长度变为两倍。