MIMO信号处理学习笔记
最近学习了MIMO雷达信号处理的部分基础知识,现将我的学习笔记与大家分享,不对之处请多指教。
本文主要包含的内容有
- MIMO雷达的发射信号
- 回波信号模型
- 双基地MIMO雷达的DOD、DOA估计
MIMO雷达的发射信号
在MIMO雷达系统中,假设有N个发射阵元构成了一个均匀线阵,以第一个阵元为参考阵元,则发射信号可写为:
s n ( t ) = u n ( t ) e − j 2 π f c t s_{n}(t)=u_{n}(t)e^{-j2\pi f_{c}t} sn(t)=un(t)e−j2πfct其中 u n ( t ) u_{n}(t) un(t)为基带正交波形, f c f_{c} fc为载频, t ∈ [ 0 , T ] t\in [0,T] t∈[0,T], T T T为脉冲宽度,PRI为脉冲重复周期。
发射信号矩阵为: S = [ s 1 ( t ) , s 2 ( t ) , . . . , s N ( t ) ] T S=[s_{1}(t),s_{2}(t),...,s_{N}(t)]^{T} S=[s1(t),s2(t),...,sN(t)]T通常在Matlab中仿真的时候,正交基带波形 u n ( t ) u_{n}(t) un(t)通过Hadamard函数实现,例如
N = 10; % 发射阵元个数
h = 64;
H = hadamard(h); %此处h必须是2的整数幂
St = (H(1:N,:)+1i*H(N+1:2*N,:))/sqrt(2); % 得到归一化的复信号矩阵,信号长度为h
回波信号模型
此部分主要涉及阵列的发射导引矩阵和接收导引矩阵
假设,收、发阵列中阵元间距均为半波长: d = λ / 2 = c / ( 2 f c ) d=\lambda /2=c/(2f_{c}) d=λ/2=c/(2fc),发射阵列有N个阵元,接收阵列有M个阵元。共有K个目标,各目标的信息为:
波离角(DOD): φ \varphi φ=[40°,20°,-30°]
波达交(DOA): θ \theta θ=[10°,50°,0°]
径向速度:vel=[100, 50, 20]
此处需要注意的是:在MIMO雷达系统中,运动速度不同的目标被称为非相干目标,运动速度相同的目标被称为相干目标。MUSIC算法及Capon算法只能估计非相干目标的参数。
因此,发射导引矩阵可以写为:
A = [ a ( φ 1 ) , a ( φ 2 ) , . . . , a ( φ K ) ] A=[a(\varphi _{1}),a(\varphi _{2}),...,a(\varphi _{K})] A=[a(φ1),a(φ2),...,a(φK)]其中
a ( φ k ) = [ 1 , e − j 2 π f c ⋅ 1 ⋅ d s i n ( φ k ) , . . . , e − j 2 π f c ⋅ ( N − 1 ) ⋅ d s i n ( φ K ) ] T a(\varphi _{k})=[1,e^{-j2\pi f_{c}\cdot 1\cdot dsin(\varphi _{k})},...,e^{-j2\pi f_{c}\cdot (N-1)\cdot dsin(\varphi _{K})}]^{T} a(φk)=[1,e−j2πfc⋅1⋅dsin(φk),...,e−j2πfc⋅(N−1)⋅dsin(φK)]T
接收导引矩阵为:
B = [ b ( θ 1 ) , b ( θ 2 ) , . . . , b ( θ K ) ] B=[b(\theta _{1}),b(\theta _{2}),...,b(\theta _{K})] B=[b(θ1),b(θ2),...,b(θK)]其中
b ( ϑ k ) = [ 1 , e − j 2 π f c ⋅ 1 ⋅ d s i n ( θ k ) , . . . , e − j 2 π f c ⋅ ( M − 1 ) ⋅ d s i n ( θ K ) ] T b(\vartheta _{k})=[1,e^{-j2\pi f_{c}\cdot 1\cdot dsin(\theta _{k})},...,e^{-j2\pi f_{c}\cdot (M-1)\cdot dsin(\theta _{K})}]^{T} b(ϑk)=[1,e−j2πfc⋅1⋅dsin(θk),...,e−j2πfc⋅(M−1)⋅dsin(θK)]T
多普勒频移为
f d k = 2 f c v k / c f_{dk}=2f_{c}v_{k}/c fdk=2fcvk/c其中 v k v_{k} vk为第k个目标的径向运动速度,当条件:
2 π f d k T ≪ 1 2\pi f_{dk}T\ll 1 2πfdkT≪1满足时,多普勒慢变化成立。即可认为同一个脉冲回波内的多普勒包络是不变的,所以第 m m m个阵元接收的回波信号为:
x m ( t ) = ∑ k = 1 K e − j 2 π f c ( m − 1 ) d s i n ( θ k ) e − j 2 π f d k l ⋅ P R I a ( φ k ) S x_{m}(t)=\sum_{k=1}^{K}e^{-j2\pi f_{c}(m-1)dsin(\theta _{k})}e^{-j2\pi f_{dk}l\cdot PRI}a(\varphi _{k})S xm(t)=k=1∑Ke−j2πfc(m−1)dsin(θk)e−j2πfdkl⋅PRIa(φk)S
信号处理-双基地MIMO雷达的DOD、DOA估计
快拍(snapshot),是ADC采集数据的一个时间窗内的采样
此处,可将一个脉冲内的ADC采样点数设为h。所以,第 l l l个快拍得到的信号矩阵为 X l X_{l} Xl,其维度为 M × h M\times h M×h。
所以,当快拍数为 L L L时,可以得到 L L L个 M × h M\times h M×h维的接收信号矩阵: X 1 , X 2 , . . . , X L X_{1}, X_{2}, ..., X_{L} X1,X2,...,XL对这 L L L个信号矩阵做匹配滤波 Y l = X l × S = e − j 2 π f d k l P R I B A T Y_{l}=X_{l}\times S=e^{-j2\pi f_{dk}lPRI}BA^{T} Yl=Xl×S=e−j2πfdklPRIBAT可以得到 L L L个 M × N M\times N M×N维的匹配滤波输出: Y 1 , Y 2 , . . . , Y L Y_{1}, Y_{2}, ...,Y_{L} Y1,Y2,...,YL 矩阵 Y l Y_{l} Yl可以成为数据矩阵
对数据矩阵做行列堆栈处理,可以得到 M N × 1 MN\times 1 MN×1维的数据列向量 y l = v e c ( Y l T ) y_{l}=vec(Y_{l}^{T}) yl=vec(YlT) L L L个数据列向量可以构成一个 M N × L MN\times L MN×L维的数据矩阵 Y ~ = [ y 1 , y 2 , . . . , y L ] \tilde{Y}=[y_{1}, y_{2}, ...,y_{L}] Y~=[y1,y2,...,yL]
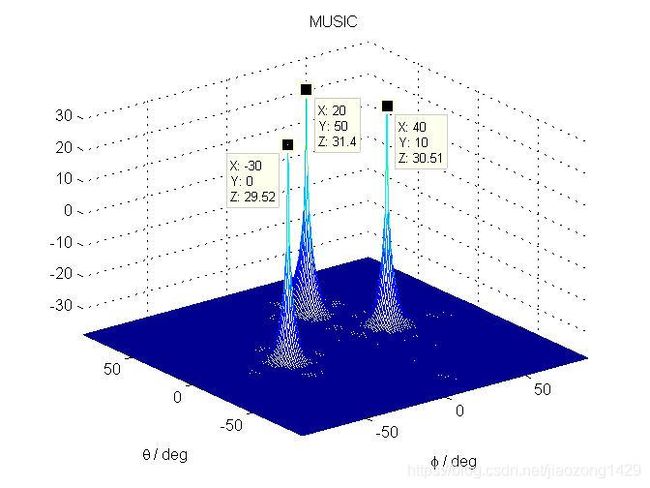
MUSIC算法
求矩阵 Y ~ \tilde{Y} Y~的协方差矩阵 R R R, R = 1 / L ∗ Y ~ ∗ Y ~ H R=1/L*\tilde Y*\tilde Y^{H} R=1/L∗Y~∗Y~HMUSIC的具体内容、推导与证明可以参考这里
在具体实现中
- 对协方差矩阵 R R R做奇异值分解 R = U S γ S U S + U N γ N U N R=U_{S}\gamma _{S}U_{S}+U_{N}\gamma _{N}U_{N} R=USγSUS+UNγNUN
[U,~,~] = svd(R);
- 求噪声子空间
UU = U(:,K+1:end); % (需要知道目标个数的先验信息)
- 谱峰搜索 P M U S I C = 1 / ∣ a ( φ , θ ) H ( U U ∗ U U H ) ∗ a ( φ , θ ) ∣ P_{MUSIC}=1/|a(\varphi ,\theta)^{H}(UU*UU^{H})*a(\varphi ,\theta)| PMUSIC=1/∣a(φ,θ)H(UU∗UUH)∗a(φ,θ)∣
n1 = (0:N-1)';
m1 = (0:M-1)';
theta = (-90:1:90)/180*pi;
phi = (-90:1:90)/180*pi;
Pmusic = zeros(length(theta),length(phi));
Pcapon = zeros(length(theta),length(phi));
for i = 1:length(theta)
for j = 1:length(phi)
A = exp(-1i*2*pi*n1*sin(phi(j))/2); % N*1
B = exp(-1i*2*pi*m1*sin(theta(i))/2); % M*1
AA = kron(B,A); % NM*1
Pmusic(i,j) = 1/abs(AA'*(UU*UU')*AA);
Pcapon(i,j) = 1/abs(AA'*Ri*AA);
end
end
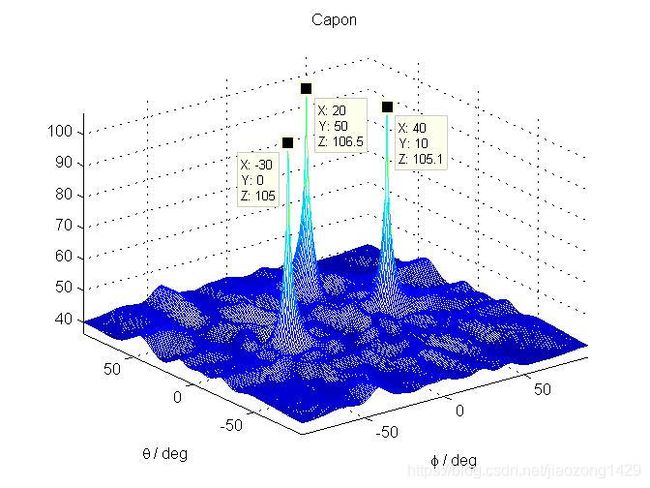
Capon算法
与MUSIC算法在实现时的不同是谱峰搜索 P C a p o n = 1 / ∣ a ( φ , θ ) H R − 1 ∗ a ( φ , θ ) ∣ P_{Capon}=1/|a(\varphi ,\theta)^{H}R^{-1}*a(\varphi ,\theta)| PCapon=1/∣a(φ,θ)HR−1∗a(φ,θ)∣