马尔可夫过程

马尔可夫过程

强化学习基于马尔可夫过程，研究的问题都可以抽象成马尔可夫过程。其定义为满足马尔可夫性质的随机过程。
马尔可夫性质：通俗来讲，即当前状态包含了所有相关的历史，只要当前的状态已知，下一个状态的发生可能性就已经确定，不需要知道从开始到当前状态所经历的具体的状态变换。
$$P(s_{t+1}|s_t)=P(s_{t+1}|s_t,s_{t-1},s_{t-2}...s_0)$$

马尔可夫过程奖励

马尔可夫过程可以用一个元组$(S,A,P,R,\gamma )$,$S$为状态空间集合，$A$为动作空间集，$P$为状态转移概率分布矩阵，$R$为各个状态$s$的奖励集，$\gamma$折扣因（0-1）
奖励（回报）
每一个状态$s$都有一个奖励值，集合为$R$，在$t$时刻从状态$s_t$开始，到这个回合（episode）结束，所能获得的奖励总和称为回报。
$$G_t=r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+{\gamma }^3{r}_{t+4}+{\gamma }^4{r}_{t+5}+...$$
$$G_t=r_{t+1}+\gamma G_{t+1}$$
其中$\gamma$为折扣因子，取值0-1，其代表的意义为，当前眼前的奖励值与未来奖励值的占比关系。从现实生活考虑，未来的回报不确定性因素高，需要打个折扣。当$\gamma$趋于1时，表示对未来的回报越看重，更加考虑未来的收益，不局限于眼前的利益。相反，趋于0时，表示注重眼前的收益。
由于每个episode所经历的状态过程是随机的，不确定性高，但是我们需要一个稳定的奖励值来指导Agent,因此我们可以对回报函数求期望，就得到一个价值函数$V(s)$。
策略
策略$\pi$是指智能体在某个时刻的状态，根据策略决策应该选择哪个动作。
确定性策略：$s$->$a$的映射，即在状态$s$，选择动作$a$的概率为1.
随机策略：$\pi (a|s)$，表示在状态$s$下，选择动作$a$的概率值，该值不一定为1，即面对状态$s$，agent依概率选择动作，则有可能会选到概率值小的动作（可能性较小而已）。

价值函数

状态的奖励$R$是状态的立即回报，是‘眼前的利益’
状态价值函数
在某一个策略$\pi$下，状态$s_t$的价值函数，即为根据这个策略，一步步走到结束，每个状态的奖励的加和期望。
$$V_{\pi }（s_t）=E_{\pi }[G_t|s_t]=E_{\pi }(r_{t+1}+\gamma G_{s_{t+1}})$$$$=E_{\pi }(r_{t+1})+E_{\pi }(\gamma G_{st+1})=R_{t+1}+\gamma V_{\pi }(s_{t+1})$$

当前状态价值，等于该状态的立即回报的期望(下一个状态是不确定，因此不能确定立即回报，要取期望)+下个状态打了折扣的价值，状态价值函数描述了该状态的好坏。
动作价值函数
在某一个策略$\pi$下，状态$s_t$，选择具体某个动作$a_t$的价值函数，即选择完动作后，一直走到结束的所有奖励加和的期望。
$$Q_{\pi }(s_t,a_t)=E_{\pi }[G_t|s_t,a_t]$$
动作价值函数描述了在状态$s_t$下，选择该动作的好坏。

状态价值函数和动作价值函数的关系

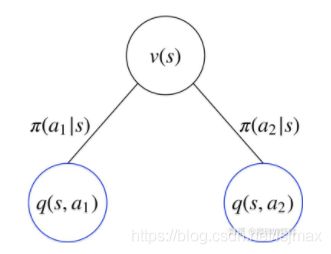
要求某个状态$s$的状态价值函数，主要考虑，从这个状态出发，一共有几个动作可以选，每个动作对应的动作价值函数的累加和就是该状态的价值。
$$V_{\pi }(s)=\sum \pi (a_i|s)q_{\pi }(s,a_i)$$
对于确定性策略，对于某个状态，选择的动作是确定的，概率是1，因此$\pi (a|s)=1$,上式就可以写成，$V_{\pi }(s)=q_{\pi }(s,a)$，状态价值函数就等于了动作价值函数。

要求某一状态下$s$下，确定选择某个动作$a$后，这个动作的价值函数，可以考虑，动作确定后，他就会转变成下一个状态，获得一个立即回报，但是转变成哪个状态是不确定的，和状态转移概率有关，因此当前动作的价值等于可能转变成的下一个状态的$s\prime$的状态价值累计和以及状态改变带来的立即回报。
$$q_{\pi }(s,a)=\sum P_{ss\prime }^a(r_i+v_{\pi }(s{\prime }_i))=R_s^a+\sum P_{ss\prime }^a{v}_{\pi }(s{\prime }_i)$$
将$q_{\pi }(s,a)$带入$V_{\pi }(s)$可以得到：
$$V_{\pi }(s)=\sum \pi (a_i|s)[R_s^a+\sum P_{ss\prime }^a{v}_{\pi }(s{\prime }_i)]$$
该方程就是贝尔曼方程(Bellman)。
用矩阵形式表示：$$V_{\pi }=R_s^a+\gamma P_{ss\prime }{V}_{\pi }$$
和$$V_{\pi }(s_t)=R_{t+1}+\gamma V_{\pi }(s_{t+1})$$
本质上是一致的，当前状态的价值=立即回报+下一个状态的价值
同理可以推出$$q_{\pi }(s,a)=R_s^a+\sum P_{ss\prime }^a\sum \pi (a_i|s\prime )q_{\pi }(s\prime ,a_i)$$
通过贝尔曼方程，当状态转移矩阵和策略已知的条件下，就可以通过迭代求出最优策略。

最优策略

对于MDP问题，一定存在一个最优策略${\pi }^{\ast }$,设该策略下的状态价值函数为$V^{\ast }(s)$,动作价值函数$Q^{\ast }(s,a)$,则有下式成立
$$Q^{\ast }(s,a)\ge Q_{\pi }(s,a),V^{\ast }(s)\ge V(s)对任意的策略\pi$$
定理：

1. 对于任何MDP，存在一个最优策略，比任何其他策略更好，或至少相等；
2. 所有的最优策略有相同的最优价值函数；
3. 所有的最优策略有相同的动作价值函数；

因此，求最优策略可以通过求最优价值函数，转换为求价值函数的最大值问题。

动态规划

动态规划是需要在状态转移概率矩阵和回报函数已知的情况下，可以通过迭代求解得到最优策略。
动态规划问题两个性质：
最优子结构：保证能够使用最优性原理(多阶段决策过程的最优决策序列具有这样的性质：不论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略),问题可以转化成求子问题最优。
子问题重叠：子问题反复出现，可以缓存子问题和重利用子问题的解。

策略迭代

给定初始策略${\pi }_k$，计算出该策略下的状态$V_{{\pi }_k}$和动作价值函数$V_{{\pi }_k}$，根据贪心策略${\pi }_{k+1}(s,a)=ma{x}_a{Q}_{{\pi }_k}(s,a)$，得到新的策略${\pi }_{k+1}$,然后在新的策略下，求出新的价值函数，反复迭代，直到价值函数和策略收敛，就求出了最优策略。
策略评估：$$V_{\pi k+1}(s)=\sum \pi (a_i|s)[R_s^a+\gamma \sum P_{ss\prime }^a{V}_{\pi k}(s{\prime }_i)]$$
即求出该策略下价值函数最终的收敛值，贝尔曼方程中，求解当前状态$s$下的价值$V_{k+1}(s)$等于立即回报+下一个状态$s\prime$的价值$V_{k+1}(s\prime )$，但是我们不知道下一个状态$s\prime$的价值$V_{k+1}(s\prime )$是多少，因此这里采用的是上一次迭代的$s\prime$的价值$V_k(s\prime )$替代。因此在一轮迭代中，可以对将所有的状态的价值函数进行更新，然后进行下一轮，直到价值收敛了，就求出了该策略下的状态价值函数。
策略改进：
对于小问题，第一轮状态价值函数更新收敛，求出某策略下的状态价值函数后，根据贪心策略，可能就能得到最终最优策略。而复杂大问题，此时根据贪心策略得到新的策略，该策略还不是最优策略，需要重新进行策略评估，然后在进行策略改进，不断进行迭代，直到策略收敛。

价值迭代

策略迭代中，需要先进行策略评估，先求出当前策略下的价值函数，在根据价值函数进行策略改进。如果将贝尔曼方程：

$$V(s)=\sum \pi (a_i|s)[R_s^a+\gamma \sum P_{ss\prime }^{a}V(s{\prime }_i)]$$改成
$$V_{k+1}(s)=ma{x}_a[R_s^a+\gamma \sum P_{ss\prime }^a{V}_k(s{\prime }_i)]$$价值迭代不涉及策略，（但是需要知道具体状态下，下一个所有的状态以及相应的转换概率）直接通过价值函数迭代逼近最优价值函数，跳过了策略改进的步骤。实际上改进过程已经通过$ma{x}_a$实现了。贝尔曼方程是求的期望，改进后的价值方程是贝尔曼优化方程。
同理，动作价值函数也有迭代公式：
$$Q_{\pi +1}(s,a)=R_s^a+\gamma \sum P_{ss\prime }^{a}ma{x}_a{Q}_{\pi }(s\prime ,a\prime )$$

广义策略迭代

在策略迭代中，策略改进，必须在策略评估迭代收敛后再进行。然而，实际上并不需要策略评估收敛后再进行策略改进，值迭代就是最极端的例子，不进行评估就进行策略改进(实际暗中是进行了策略评估的一次更新)，同样也可以得到最优策略。因此还有很多介于两者之间的方法，只要所有的状态价值和策略在不断地更新迭代，则最终一定会收敛到最优价值函数和最优策略，称为广义策略迭代。即只强调价值函数和策略在不断迭代提升，不关注具体的细节。强化学习都可以很好地描述成广义策略迭代。