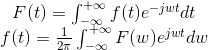学习matlab（七）——符号计算

在MATLAB中，提供了强大的符号运算功能，并且有专门的符号数学工具箱Symbolic Math Toolbox。此外，在MATLAB中，还可以通过maple. m和map. m两个接口和Maple相连。MATLAB的符号计算功能非常强大。在MATLAB中，符号计算的函数主要分为以下几类:符号表达式、符号矩阵操作、符号微积分、符号积分变换、符号方程求解、符号函数的绘图、图形化符号函数计算器

符号数学工具箱中定义了一种新的数据类型: sym类。sym类的实例就是符号对象，用来存储代表符号的字符串在MATLAB中，提供了两个建立符号对象的函数:函数sym( )和函数syms( ),两个函数的用法不同。

在MATLAB中，可以利用函数sym( )建立单个的符号变量。采用函数syms( )一次定义多个符号变量。此外，可以通过函数class()获取符号变量的类型。对于'r'，默认设置，为最接近的有理数表示；对于‘d’，为最接近的十进制浮点数32位表示；syms x y也可以定义两个符号变量。

在老版本的matlab可以直接用符号变量表达式，新版本会警告（我这里是matlab2016为例测试的）；

0.符号函数和符号方程

在MATLAB中，符号表达式是由符号常量、符号变量、符号函数运算符以及专用函数连接起来的符号对象。符号表达式有两类:符号函数和符号方程。方程与函数的区别为:函数是一个代数式, 而方程是一个等式。对于一元二次方程，, 其中a≠0,根据一元二次方程的求根公式,得到方程的两个根。当时，该方程有实根，该方程有实根;当时， 方程有两个共轭的复根。在MATLAB中,利用函数diff()来求导数。根据复合函数的求导公式进行计算。在MATLAB中，利用函数int( )求不定积分。在MATLAB中，利用函数int( )求不定积分。求解微分方程dy/dt=ay,该方程为可分离变量微分方程，进行变量分离，然后进行积分。采用函数dsolve( )求解微分方程。

>> x1 = solve('a*x^2+b*x+c=0');//方程求解
 
>> syms x;
>> y = diff(x^5*cos(x)+cos(pi/6));//表达式求导


>> syms x;
>> y = int(exp(sin(x))*cos(x),'x');//表达式进行不定积分

>> syms x;
>> y = int('sin(x)',x,0,pi);//表达式进行定积分

1.运算精度

在MATLAB中，采用函数digits( )和vpa( )来实现任意精度的符号运算。下面分别进行介绍:digits(d):调用该函数后，符号对象的近似解的精度变成d位有效数字,参数d的默认值为32位。D=digits:调用该函数后，得到当前采用的数值计算的精度。R=vpa(A):该函数计算符号矩阵A的近似解，精度为函数digits(d)指定的有效位数。R=vpa(A,d):该函数计算符号矩阵A的近似解，有效位数由参数d决定。

在MATLAB中，采用了函数重载技术，使得符号表达式的运算符和基本函数与数值计算中的运算符和基本函数几乎完全相同。符号表达式可以进行“+”、“-”、“*”、“/”四则运算。符号表达式的比较中，只有运算符“= =”和“~ ="代表“等于”和“不等于”。当结果为“真”时，返回值为1,否则返回值为0。

符号表达式的常用操作，包括:利用函数findsym( )寻找符号变量。利用函数factor()进行符号多项式的因式分解。利用函数expand()进行符号表达式的展开。利用函数collect( )进行符号表达式中同类项的合并。利用函数horner()将符号多项式转换成嵌套形式。利用函数numden( )获取符号表达式的分子和分母。

在MATLAB中，采用函数simplify( )和函数simple( )进行符号表达式的化简，下面分别进行介绍。函数simplify( )是一个具有普遍意义的工具,能够对包含和式、方根、分数的乘方、指数函数、对数函数、三角函数等的表达式进行化简。函数simple()也能进行符号表达式的化简，该方法比函数simplify()要简单，所得到的结果也比较合理。

在MATLAB中，可以采用函数subexpr( )和函数subs( )进行符号替换，让符号表达式的输出变的简单。函数subexpr()将符号表达式中重复出现的字符串用变量代替。函数subs()将符号表达式中重复出现的字符串用数值或字符串替换。

在MATLAB中，采用函数finverse( )进行反函数运算。该函数的调用格式为:g=finverse(f):该函数将会计算输入参数f的反函数,其中f为符号表达式，以默认的变量为自变量。函数的返回值g也是一个符号表达式。g=finverse(f, v):输入参数v是-一个符号变量，是函数f中的变量，且该函数的返回值g以v为自变量。

在数学计算中，经常会遇到求复合函数的情况。例如,函数z=f(y),而该函数的自变量y又是一个关于x的函数,即y=g(X)。此时，z=f(g(X)), z是关于x的一一个复合函数。在MATLAB中，采用函数compose( )进行符合函数运算。

2.符号矩阵

符号矩阵也是一种符号表达式，前面介绍的符号表达式运算都可以用于符号矩阵，需要注意的是这些函数作用于符号矩阵时，是分别作用于矩阵的每一个元素。由于符号矩阵是一个矩阵，所以符号矩阵还能进行有关矩阵的运算。此外，曾介绍过的许多应用于数值矩阵的函数，也可直接应用于符号矩阵。

在MATLAB中，可以采用函数sym( )直接产生符号矩阵,也可以将数值矩阵转换为符号矩阵。下面介绍如何生成符号矩阵：

1.采用函数sym()直接生成符号矩阵

2.利用函数sym()将数值型变量转换为符号型变量

对于符号变量和的四则运算有:A+B和A-B:实现符号矩阵的加法和减法。如果A和B为同类型的矩阵(具有相同的行数和列数)时，分别对对应的元素进行加减运算。如果A和B中有一个为标量，则矩阵中的每一个元素和该标量进行加法或减法。A*B:实现矩阵A和B的乘法，要求矩阵A的列数必须等于矩阵B的行数。如果A和B中有一个为标量，则将矩阵中的每一个元素乘以该标量。A\B:实现矩阵的左除法。X=AIB为符号线性方程组A*X=B的解。另外，A\B近似等于inv(A)*B。如果X不存在或不唯一，则系统显示警告信息。B/A:实现矩阵的右除法。X=B/A为符号线性方程组X*A=B的解。B/A近似为B*inv(A)。如果X不存在或不唯一，则系统显示警告信息。

符号矩阵和数值矩阵非常的类似，也可以求符号矩阵的转置秩、逆矩阵、行列式和特征值分解等。下面进行详细的介绍。

1.符号矩阵的转置2.符号方阵的幂运算3.符号矩阵的秩4.符号方阵的逆矩阵和行列式计算5.符号方阵的特征值分解6.约当标准型7.符号矩阵的奇异值分解

3.复杂运算

在MATLAB中，采用函数diff( )进行微分和求导运算,利用Jacobian函数jacobian( )实现对多元符号函数的求导。在MATLAB中，采用函数limit( )求符号表达式的极限。

在MATLAB中，采用函数int( )来计算符号表达式的不定积分和定积分。该函数的调用格式为:R=int(S):该函数计算S的不定积分,输入参数S可以是符号表达式或符号矩阵。没有指定积分变量和积分阶数，系统按函数findsym()得到的默认变量对S求不定积分。R=int(S, v):该函数对S中指定的符号变量v求不定积分。需要注意的是，函数的返回值R只是其中的一个原函数，后面没有带任意常数C。R=int(S, a, b):该函数计算S在闭区间[a, b]上的定积分。由于没有指定积分变量，系统按函数finldsym( )得到的默认变量计算定积分。a和b分别表示定积分的下限和上限,可以是两个具体的数，也可以是一一个符号表达式，还可以是无穷大(inf )。R=int(S, V, a, b):该函数计算S对于变量v在区间[a, b]上的定积分。

符号运算不仅能够求解方程,还可以求解方程组。下面介绍如何利用函数solve( )求解符号代数方程组，函数dsolve()求解微分方程组。在MATL AB中，利用函数solve( )求解一般符号代数方程组。该函数的调用格式为:solve('eqn1'):该函数求解单个的方程eqn1。solve('eqn1', 'eqn2', ... 'eqnN):该函数用来求解由N个方程组成的方程组。solve('eqn1', 'eqn2', ... 'eqnN', 'var1', 'var2', ... 'varN'):该函数中var1等表示符号变量，以这些变量为自变量,进行方程的求解。

在MATLAB中，采用函数dsolve()进行微分方程的求解。该函数的调用格式为:dsolve('eq1'):该函数对单个的微分方程eq1求解。dsolve('eq1, eq2, ..'‘cond1, cond2, ..’, ‘V'):该函数对由eq1,eq2等组成的微分方程组求解，初始条件为cond1, cond2deng，自变量为V。如果不指定参数v,则系统默认以t为自变量。

（0）级数求和

在MATLAB中，采用函数symsum( )进行级数符号的求和。该函数的调用格式为:symsum(S):该函数没有指定求和的符号变量，参数S表示级数的通项。symsum(S, V):该函数对变量v进行级数求和。symsum(S, a, b):该函数对默认变量从a到b进行级数求和。symsum(S, V, a, b):该函数对于变量v从a到b进行级数求和。

在MATLAB中，采用函数taylor( )求符号表达式的泰勒级数展开式，该函数的调用格式为:taylor(f):计算函数f在默认变量等于0处作默认为5阶的泰勒展开式。taylor(f,n):计算函数f在默认变量为0处做n-1阶的泰勒展开式的默认值为6。taylor(f,a):计算函数f在默认变量等于a处做默认为5阶的泰勒展开式，a的默认值为0。taylor(f, n, a):计算函数f在默认变量等于a处做n-1阶的泰勒展开式。taylor(f, n, v, a);计算函数f在变量等于a处做n-1阶的泰勒展开式，变量变为V。

（1）傅里叶变换

时域中的信号f(t)与它在频域中的Fourier变换F(w)之间存在如下的关系。

在MATLAB中，采用函数fourier( )计算傅立叶变换，采用函数ifourier( )计算傅立叶变换的反变换。

（2）拉普拉斯变换

对于函数f(x)进行拉普拉斯(Laplace)变换的公式为:

对函数L(s)进行拉普拉斯反变换的公式为:

在MATLAB中，实现拉普拉斯变换的函数为laplace(),进行拉普拉斯反变换的函数为ilaplace()。

（3）Z变换

对于离散序列f(n)的Z变换为：

对于F(z)的Z反变换为:

在MATLAB中，利用函数ztrans( )进行Z变换，利用函数iztrans( )进行Z反变换。

4.绘图

在MATLAB中，对于符号方程,可以非常方便的绘制其图形。本节将介绍符号函数的图形绘制，常用的绘图函数如表所示：

函数名	函数的功能
fplot	一元函数绘图
ezplot	二元函数绘图
ezpolar	极坐标系下的绘图
ezplot3	三维图形
ezmesh	三维网格图
ezmeshc	带等值线的三维网格图
ezcontour	等值线图
ezcontourf	带填充的等值线图
ezsurf	三维彩色曲面图
ezsurfc	带等值线的三维彩色曲面图

在MATLAB中，提供了图形化的符号函数计算器。图形化的符号函数计算器功能虽然不是十分的强大，但是操作非常简单和方便，用户可以可以对符号运算和函数图形有个直观的了解。在MATLAB中，有两种符号函数计算器，单变量符号函数计算器和泰勒汲数逼近计算器，下面分别进行介绍。

在MATLAB中，可以使用函数funtool来调用图形化的单变量符号函数计算器。用户在命令行窗口中输入:funtool,可将单变量符号函数计算器调出，包括3个图形窗口。

在MATLAB中，可以使用函数taylortool来调用图形化的泰勒级数逼近计算器。用户在命令行窗口中输入:taylortool,即可将泰勒级数逼近计算器调出。泰勒级数逼近计算器是一个交互的界面，可以绘制函数f(x)前N阶的泰勒级数。系统默认的函数为f(x)=x*cos(x),泰勒级数展开的阶数为7，自变量的默认区间为[-2*pi, 2* pi]。

5.Maple接口

为了在MATLAB中进一步利用Maple的符号计算能力,MATLAB的符号数学工具箱提供了两个函数:函数sym()和函数maple( )。这两个函数能够实现对Maple中绝大多数符号计算函数的调用，利用它们可以扩充MATLAB的符号计算能力，下面分别进行介绍。

在MATLAB中，可以采用函数sym( )来调用Maple函数,来扩充MATLAB的符号计算功能。然后，通过函数subs( )进行变量的替换。

在MATLAB中，可以采用函数maple( )调用Maple中的函数。在MATLAB中可以通过函数mhelp来获得Maple函数的帮助信息。例如，在命令行输入: mhelp gcd,将获取Maple中的函数gcd的帮助信息。函数gcd()用于求两个多项式或整数的最大公约数。