【机器学习】 强化学习
强化学习实际上是找一个从观测到动作的最优映射函数,输入是外界观测,目标是奖励最大化。
强化学习的主要特点:
- 学习过程中没有监督信号,只要奖励(reward)
- 其反馈(feedback)是延迟的而非瞬间的
- 强化学习过程与时间序列相关,是一个序贯决策的过程
- agent采取的动作(action)会影响到它所接受的序列数据
强化学习算法分类:
- model-free RL(不理解环境):不具备环境的先验知识,所以只能通过与环境的不断交互来积累经验来进行相应的学习。
- model-based RL(理解环境):agent非常了解有关环境的各种情况,比如说状态到状态之间是怎样转换的,以多大的概率进行转换,在某一个状态上执行某个动作可以获得什么样的立即回报。这样一来,agent可以根据对环境的先验知识进行相关的学习和推理。
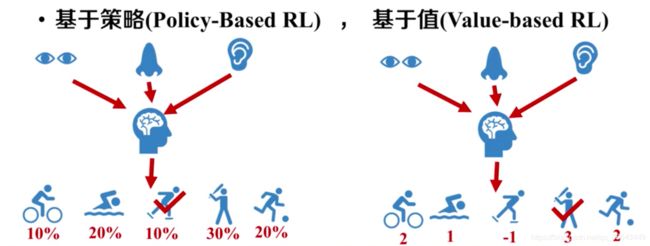
- policy-based RL(基于策略):可以通过对状态的价值的评估来选取相应的动作执行,根据概率进行动作的选择,所以即使在某个动作上的概率值很大,但是在真正执行的过程中,基于策略的强化学习方法也不一定真的能够选取到这个动作。当动作是连续的情况下,可以采用基于策略的强化学习算法来进行学习和推演,因为基于策略的强化学习方法是可以用概率来选择某一个特定动作的。
- value-based RL(基于值):可以通过对状态的价值的评估来选取相应的动作执行。如果动作是连续的而不是离散的,基于值的方法就无法解决这个问题。
- on-policy(在线学习):边执行动作边学习的学习方法,对于agent和系统的交互过程中所选择的动作以及在计算评估函数的过程中所选择的动作,这两套策略是完全一致的。
- off-policy(离线学习):通过自己或他人的经验进行学习的一种方法。交互所选择的动作和更新函数值所选择的动作所采取的策略是不一样的。
- mente-carlo update(回合更新):只有在每一个回合结束之后,才去回顾相应的经验,进而调整策略。
- temporal-difference update(单步更新):在每一步的决策过程中,都想办法调整策略。


【马尔可夫决策过程(MDP)】
马尔可夫性:系统的下一个状态仅与当前状态有关,而与以前的状态无关。
马尔可夫过程:马尔可夫过程是一个二元组(S,P),且满足S是有限状态集合,P是状态转移概率。给定转移概率时,从某状态出发存在多条马尔可夫链。


马尔可夫决策过程优元组(S,A,P,R,γ)描述,其中:
- S为有限的状态集
- A为有限的动作集
- P为状态转移概率
- R为回报函数
- γ为折扣因子,用来计算累积回报
与马尔可夫过程不同,其状态转移概率包含动作,即
![]()


当γ取0的时候,我们期待的是一个短期的回报,当γ取1的时候,我们期待的是一个比较长期的回报。

状态值回报是在给定状态的情况下,计算累积回报的数学期望。
状态-动作值函数是在给定状态和动作的情况下,计算累积回报的数学期望。

有了贝尔曼方程,就可以借鉴动态规划的思想,可以将状态值函数和状态-动作值函数通过累积的方法迭代进行计算。

左上角和右下角是我们希望能达到的目标状态。在每一个动作(上下左右移动一次)执行后都可以得到一个立即回报R=-1
目标是想尽快地到达目标状态。
【策略迭代】
策略迭代分为两个过程:策略评估和策略更新。
策略评估:在当前的策略中更新各状态的值函数,即我们现在有一个给定的当前策略,我们通过当前的策略来选择动作,来更新相应的值函数。如果达到迭代次数或者值函数收敛就不再迭代。
策略更新:基于当前值函数得到最优策略。

基于策略评估,有四个策略进行了更新,是因为使用这四个动作后,都可以从当前的状态带到另外一个值函数比较高的状态之上。

第一行的 -1.7 =0.25(-1+0) + 0.25(-1±1) + 0.25(-1±1) + 0.25(-1±1)

策略迭代的缺点:如果策略空间很大,策略评估就会很耗时
【值迭代】
每次值迭代都找到让当前值函数最大的更新方式,并且用这种方式更新值函数,直到值函数不再变化。




二者比较:
- 策略迭代是累积平均的计算方式,值迭代是单步最好的方式
- 值迭代速度更快,尤其是在策略空间较大的时候
- 策略迭代更接近于样本的真是分布
【探索与利用】
利用:做你当前知道的能产生最大回报的事情。
探索:做你以前从来没有做过的事情,以期望获得更高的回报。

具体描述为:首先要给一个比较小的值 ε,然后我们可以通过一个分布来取得一个概率,通常情况下可以使用均匀分布区选择一个概率。如果概率小于 ε,就为强化学习执行一个随机动作;如果取出来的概率大于 ε,则选择刚才已经选好的最优的策略。由于在这个过程中,我们采取了随机的操作,就起到了一个探索的作用。
好处:
- 计算容易,不需要复杂的计算公式
- 能保证充分探索所有状态
坏处:
- 需要大量探索,数据利用率低
- 需要无限长时间(取决于壮体啊的数量以及 ε的大小)
除了 ε-greedy策略意外,还有其他策略,比如玻尔兹曼机策略和高斯策略,这两种策略和 ε-greedy的本质其实都是一致的,都是需要在一个确定性的策略上加一个随机的扰动。
以上方法都是model-based方法,接下来是model-free方法:
【蒙特卡洛方法】
为什么要采用monte carlo方法?
马尔可夫决策过程是典型的model-base方法,也就是说我们知道关于这个环境状态之间转换的关系以及他们的转换概率以及回报函数,但是对于大多数情况,我们是不知道环境的相关信息的,不清楚真实的状态转移概率或者即时奖励。
思想:在不知道环境相关信息的情况下,我们通常要对某一个状态的价值进行评估。通常情况下某个状态的价值等于在多个episode(每条episode就是一条从起始状态到结束状态的经历)中以该状态算得的所有奖励的平均。
蒙特卡洛的两种方法:
-first-visit:在计算状态s处的值函数时,只利用每个episode中第一次访问到状态s时返回的值。
-every-visit:在计算状态s处的值函数时,利用所有访问到状态s时的奖励返回值。

【时序差分学习TD-learning】
蒙特卡洛需要等到整个episode结束才能更新,且一定要有很多episode,蒙特卡洛方法才能够执行,需要大量的episode才能得到较为准确的结果。

时序差分可以认为是:假设agent向前走一步,用未来一步的回报去更新当前的值函数。步长可以取1、2、…、∞,如果当步长等于∞的时候,时序差分就等价于蒙特卡洛。

从偏差和方差的角度来说,由于蒙特卡洛算法是考虑了所有的episode并且很多步以后的回报都会被考虑到当前步的回报当中,所以它的计算偏差是0,但是由于采样的episode不尽相同,或者采样的episode的数目不够大,就导致了蒙特卡洛算法的方差很大。相比之下,时序差分算法由于考虑到状态之间的转换,也采用了一些概率上更新的方法,所以它的方法相对于较低,但是有偏差。
接下来是TD-learning的两个延伸算法,分别是Q-learning和Sarsa算法。
【Q-learning】
Q-learning是一种典型的off-policy(离线)学习算法。


我们要在Q-learning算法中维护一个Q值表。Q表的初值为:

我们要注意的是,对于这样一个model-free的问题,agent可能事先知道或者不知道state的个数。当agent知道state的个数时,我们可以把Q值表的行和列完全复制成reward fuction的行和列;当agent不知道state的个数时,那么在每一次和系统的交互过程中,如果agent认为它到达了一个新的状态,就为Q值表再新增加一行。算法的流程为:

在状态S’时,只是计算了在S‘时要采取哪一个a能得到更大的Q值,但是实际上并没有真正的执行actionA。这也说明我们在选择动作执行和计算Q-tabel的时候,采取的策略是不一样的,这也是off-policy的一个典型特征。
学习率看作是保留多少旧值、生成新值的度量。如果学习率越大,新估计值代替旧估计值的比例越大。当学习率为1时,新估值完全代替旧值,旧Q值被完全抛弃。此时(学习率为1),Q-learning更新规则如下:

就上面逃离密室的例子:


第一个episode结束,假设第二个episode开始的时候,处于状态3,在状态3的时候,可以执行动作1,2,4,假设在状态3的时候执行状态1,则有:

循环往复以上操作,最终Q值表收敛为:
我们就可以用此Q值表来得到最佳策略。下图描述了在每一个状态下执行什么样的动作才会获得最好的回报。红线标示出的序列就是对此问题的最好的决策。

【Sarsa算法】
Sarsa算法的算法流程为:

我们可以看到,在初始化和选择动作的过程中,跟Q-learning算法都是非常类似的,跟Q-learning算法不同的是Q值表的更新,在更新Q值表的时候利用的是A‘,A’是用当前的Q值表,利用Q值表能推演出来的policy(也就是它的策略)选择的。

对于Sarsa算法而言,动作的执行和更新Q值表的策略都是ε-greedy策略;但是对于Q-learning而言,执行动作我们用的是ε-greedy,但是更新Q值表我们实际上用的是贪婪策略,就是我们选择能够使Q(S’, a)最大的那个a来进行Q值表的更新。
所以一般情况下,如果是在一个仿真系统来进行强化学习的训练的时候,我们通常采用Q-learning算法;但是对于一些实际的生产问题,我们通常采用Sarsa算法,因为Sarsa算法使用了两次ε-greedy,相当于它有一些更好的探索能力。
【深度强化学习(DQN)】
Q-learning的缺陷:对于对于实际的问题,其状态和动作十分庞大,计算机的内存无法处理。


对于深度强化学习的神经网络而言,其损失函数可以设计成老的Q值和更新的Q值之间的均方差。
Target Network
DQN在进行loss function的计算中,可以不用现在的参数,而使用之前更新的参数来进行计算,计算过程为:
在一定的迭代次数后,将左边的网络完完整整的copy一份,复制成另外一份网络,叫做target-Q network,左边的网络叫做当前网络,当前网络不断地用样本来保持更新,target-Q network里的参数不进行任何的调整,。
但是在左边的当前网络进行迭代更新计算的过程中,其target的值是可以利用target-Q network里保存的有关左边网络的参数进行计算的,我们用target-Q network的参数来计算target值,然后把target值回传给左边的当前网络,让它继续进行迭代更新。
再更新一段过程之后,或者是再更新一些迭代次数之后,再把target-Q network替换成当前的Q网络,也就是再复制一次左边的当前网络,复制到target-Q network。
这样做的原因是因为比如说target游戏的图像在很多连续帧上有很强的相似性,当我们在改变当前网络参数的时候,可能把很相似的S‘的state的Q值也做了相应的更新,这样会导致训练的不稳定;另外一个原因是神经网络本身的问题,比如说神经网络进行了更新和调整,有一些Q值就一定做到了相应的改变,但实际上有一些Q值是我们不想更新的,但是因为神经网络的性质,导致那些不想更新的Q值不可避免地进行了更新,这就导致了神经网络训练的不稳定性。
在实践中,经常用Huber loss代替均方误差损失函数。Huber loss是对损失比较平滑的一种计算方式,由于均方差很容易被比较大的reward或比较小的reward带偏。使用Huber loss就可以使训练过程很逐步的进行调整,也会得到比较稳定的训练效果。
参考资料:机器学习-北京理工大学-中国大学mooc