建模方法(七)-中心化处理和标准化处理
一、中心化(又叫零均值化)和标准化(又叫归一化)概念及目的?
1、在回归问题和一些机器学习算法中,以及训练神经网络的过程中,通常需要对原始数据进行中心化(Zero-centered或者Mean-subtraction(subtraction表示减去))处理和标准化(Standardization或Normalization)处理
数据标准化(归一化)处理是数据挖掘的一项基础工作,不同评价指标往往具有不同的量纲(量纲简单理解:国际单位制中的基本单位就是基本量纲,合成量纲为基本量纲的幂积运算)和量纲单位,这样的情况会影响到数据分析的结果,为了消除指标之间的量纲影响,需要进行数据标准化处理,以解决数据指标之间的可比性。原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价。
意义:数据中心化和标准化在回归分析中是取消由于量纲不同、自身变异或者数值相差较大所引起的误差。
原理:
数据标准化:是指数值减去均值,再除以标准差;
数据中心化:是指变量减去它的均值。
目的:通过中心化和标准化处理,得到均值为0,标准差为1的服从标准正态分布的数据。
2、(1)中心化(零均值化)后的数据均值为零
(2)z-score 标准化后的数据均值为0,标准差为1(方差也为1)
三、下面解释一下为什么需要使用这些数据预处理步骤。
在一些实际问题中,我们得到的样本数据都是多个维度的,即一个样本是用多个特征来表征的。比如在预测房价的问题中,影响房价的因素有房子面积、卧室数量等,我们得到的样本数据就是这样一些样本点,这里的、又被称为特征。很显然,这些特征的量纲和数值得量级都是不一样的,在预测房价时,如果直接使用原始的数据值,那么他们对房价的影响程度将是不一样的,而通过标准化处理,可以使得不同的特征具有相同的尺度(Scale)。简言之,当原始数据不同维度上的特征的尺度(单位)不一致时,需要标准化步骤对数据进行预处理。
下图中以二维数据为例:左图表示的是原始数据;中间的是中心化后的数据,数据被移动大原点周围;右图将中心化后的数据除以标准差,得到为标准化的数据,可以看出每个维度上的尺度是一致的(红色线段的长度表示尺度)。
其实,在不同的问题中,中心化和标准化有着不同的意义,

比如在训练神经网络的过程中,通过将数据标准化,能够加速权重参数的收敛。
对于神经网络(主要是全连接网络+SGD)的学习训练,标准化有什么好处(加速收敛),以及为什么有这样的好处。另需说明的是:神经网络模型多变复杂,这里多是对于一般情况的启发性讨论,实际使用中需要具体情况具体分析(例如图像领域大多仅减均值,不除方差)。
神经网络为什么需要标准化:
简要地说,为了保证网络可以良好的收敛,在不清楚各个维度的相对重要程度之前,标准化使得输入的各个维度分布相近,从而允许我们在网络训练过程中,对各个维度“一视同仁”(即设置相同的学习率、正则项系数、权重初始化、以及激活函数)。反过来,当我们使用全局相同的学习率、权重初始化、以及激活函数等网络设置时,方差更大的维度将获得更多的重视。
网络设置, BP(逆向传播算法), SGD(梯度下降算法)简介:

· 对数据进行中心化预处理,这样做的目的是要增加基向量的正交性。
四、归一化
两个优点:
1)归一化后加快了梯度下降求最优解的速度;
2)归一化有可能提高精度。
1、 归一化为什么能提高梯度下降法求解最优解的速度?
如下图所示,蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征X1和X2的区间相差非常大,X1区间是[0,2000],X2区间是 [1,5],其所形成的等高线非常尖。当使用梯度下降法寻求最优解时,很有可能走“之字型”路线(垂直等高线走),从而导致需要迭代很多次才能收敛;而右图对两个原始特征进行了归一化,其对应的等高线显得很圆,在梯度下降进行求解时能较快的收敛。因此如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛。

注:等高线是相同目标函数值的线,即用一个平行于自变量平面的面去截取曲面得到交线,此交线即为等高线。
2、归一化有可能提高精度
一些分类器需要计算样本之间的距离(如欧氏距离),例如KNN。如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)。
3、以下是两种常用的归一化方法:
1)min-max标准化(Min-MaxNormalization)
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 - 1]之间。转换函数如下:
其中max为样本数据的最大值,min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
2)Z-score标准化(0-1标准化)方法
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1。
转化函数为:
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。
五、中心化(以PCA为例)
下面两幅图是数据做中心化(centering)前后的对比,可以看到其实就是一个平移的过程,平移后所有数据的中心是(0,0).
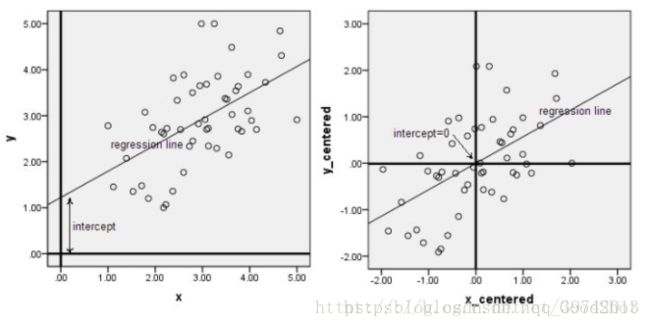
在做PCA的时候,我们需要找出矩阵的特征向量,也就是主成分(PC)。比如说找到的第一个特征向量是a = [1, 2],a在坐标平面上就是从原点出发到点 (1,2)的一个向量。
如果没有对数据做中心化,那算出来的第一主成分的方向可能就不是一个可以“描述”(或者说“概括”)数据的方向了。还是看图比较清楚。
黑色线就是第一主成分的方向。只有中心化数据之后,计算得到的方向才2能比较好的“概括”原来的数据。
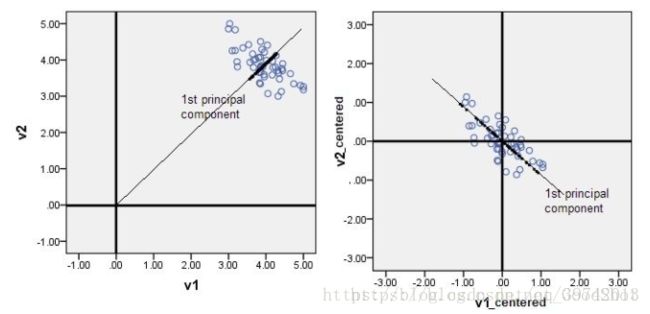
v1表示未中心化,v1_centered中心化后。
参考自
https://blog.csdn.net/silent56_th/article/details/80987837
https://blog.csdn.net/GoodShot/article/details/80373372
