常微分方程(Ordinary Differential Equation I)
常微分方程
- 微分方程基本概念
- 一阶常微分方程
- 可分离变量方程
- 变量替换法
- 一阶线性微分方程
- 恰当方程
- 积分因子法
- 等角轨线族
- 一阶隐式微分方程
- 解的存在和唯一性定理
- 解的存在和唯一性定理
- 解的延拓
- 解对初值与参数的连续性和可微性
- 奇解和包络
常微分方程(Ordinary Differential Equation I)
常微分方程(Ordinary Differential Equation II)
常微分方程(Ordinary Differential Equation III)
微分方程基本概念
微分方程:包含未知函数及其导数的方程叫做微分方程(Differential Equation)。未知函数导数的最高阶数称为该微分方程的阶(order)。
-
常微分方程(ODE):若未知函数是一元函数的微分方程称为常微分方程(Ordinary Differential Equation, ODE) 。
一般的 n 阶常微分方程的形式(也称隐式表达式)为
F ( x , y , y ′ , y ′ ′ , … , y ( n ) ) = 0 (1) F(x,y,y',y'',\dots,y^{(n)})=0 \tag{1} F(x,y,y′,y′′,…,y(n))=0(1)
如果微分方程是关于未知函数及各阶导数的线性表达式
y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x ) y ′ + a n ( x ) y = f ( x ) (2) y^{(n)}+a_1(x)y^{(n-1)}+\cdots+a_{n-1}(x)y'+a_n(x)y=f(x)\tag{2} y(n)+a1(x)y(n−1)+⋯+an−1(x)y′+an(x)y=f(x)(2)
则称为 n 阶线性(linearity)常微分方程。 -
偏微分方程(PDE):若未知函数是多元函数,方程中含有自变量的偏微分,称之为偏微分方程(Partial Differential Equations, PDE)。
如 ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ∂ 2 T ∂ z 2 = 0 \cfrac{∂^2T}{∂x^2}+\cfrac{∂^2T}{∂y^2}+\cfrac{∂^2T}{∂z^2}=0 ∂x2∂2T+∂y2∂2T+∂z2∂2T=0
微分方程的解:如果将一个函数 y = φ ( x ) y=φ(x) y=φ(x)其各阶导数代入微分方程 (1) 得到恒等式
F ( x , φ ( x ) , φ ′ ( x ) , φ ′ ′ ( x ) , … , φ ( n ) ( x ) ) ≡ 0 F(x,φ(x),φ'(x),φ''(x),\dots,φ^{(n)}(x))\equiv0 F(x,φ(x),φ′(x),φ′′(x),…,φ(n)(x))≡0
则称 y = φ ( x ) y=φ(x) y=φ(x)为上述方程的一个解(solution)。
- 通解:n 阶微分方程 (1) 的解 y = φ ( x , C 1 , C 2 , ⋯ , C n ) y=φ(x,C_1,C_2,\cdots,C_n) y=φ(x,C1,C2,⋯,Cn) 含有 n 个相互独立1的任意常数 C 1 , C 2 , ⋯ , C n C_1,C_2,\cdots,C_n C1,C2,⋯,Cn ,则称为该微分方程的通解(general solution)。
- 特解:我们称不包含任意常数的解为特解(particular solution)。
- 初值问题:通常为了解决实际问题,确定常数的值,需要引入初值条件(initial conditions)。初值条件联合微分方程组成初值问题(Initial Value Problem, IVP),或称柯西问题。
一阶常微分方程的初值问题通常记作 { y ′ = f ( x , y ) y ( x 0 ) = y 0 \begin{cases}y'=f(x,y) \\ y(x_0)=y_0\end{cases} {y′=f(x,y)y(x0)=y0 - 隐式解与隐式通解:如果关系式 Φ ( x , y ) = 0 \Phi(x,y)=0 Φ(x,y)=0 所确定的隐函数 y = φ ( x ) y=φ(x) y=φ(x) 为微分方程 (1) 的解,则称 Φ ( x , y ) = 0 \Phi(x,y)=0 Φ(x,y)=0 是方程的一个隐式解(implicit solution)。对于含有 n个相互独立常数的解 Φ ( x , y , C 1 , C 2 , ⋯ , C n ) = 0 \Phi(x,y,C_1,C_2,\cdots,C_n)=0 Φ(x,y,C1,C2,⋯,Cn)=0 为隐式通解。
解的几何意义
-
积分曲线:微分方程的解对应的曲线称为积分曲线(integral curve)。
对于一阶微分方程初值问题 { y ′ = f ( x , y ) y ( x 0 ) = y 0 \begin{cases}y'=f(x,y) \\ y(x_0)=y_0\end{cases} {y′=f(x,y)y(x0)=y0 的解对应过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的一条积分曲线,该曲线在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 处的切线的斜率为 f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0),切线方程为 y = y 0 + f ( x 0 , y 0 ) ( x − x 0 ) y=y_0+f(x_0,y_0)(x-x_0) y=y0+f(x0,y0)(x−x0)
若不给定初始条件,微分方程的通解在几何上对应着一族积分曲线,称为积分曲线族(family of integral curves)。 -
线素场:考虑微分方程 y ′ = f ( x , y ) y'=f(x,y) y′=f(x,y),若 f ( x , y ) f(x,y) f(x,y) 的定义域为平面区域G,在G 内每一点 P ( x , y ) P(x,y) P(x,y) 作斜率为 f ( x , y ) f(x,y) f(x,y) 的单位线段,则称该线段为点 P ( x , y ) P(x,y) P(x,y)的线素。G 内所有的线素构成由微分方程确定的线素场(line element field)或方向场(direction field)。
在构造微分方程 y ′ = f ( x , y ) y'=f(x,y) y′=f(x,y) 的线素场时,通常利用斜率关系式 f ( x , y ) = k f(x,y)=k f(x,y)=k 确定曲线 L k L_k Lk,称它为线素场的等斜线(isocline)。显然,等斜线 L k L_k Lk上各点的斜率都等于 k k k,简化了线素场逐点构造的方法。 -
奇异点:设一阶微分方程为 P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)dx+Q(x,y)dy=0 P(x,y)dx+Q(x,y)dy=0,函数 P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P(x,y),Q(x,y)在区域G是连续的,若 P ( x 0 , y 0 ) = Q ( x 0 , y 0 ) = 0 , ( x 0 , y 0 ) ∈ G P(x_0,y_0)=Q(x_0,y_0)=0,(x_0,y_0)\in G P(x0,y0)=Q(x0,y0)=0,(x0,y0)∈G,线素场在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处便失去意义,我们称这样的点为奇异点(singular point)。
- 示例:作微分方程 y ′ = y / x y'=y/x y′=y/x 和 y ′ = − x / y y'=-x/y y′=−x/y的线素场。
(1) y ′ = y / x y'=y/x y′=y/x 的等斜线为 L k : y = k x L_k:y=kx Lk:y=kx,说明线素斜率为 k 的所有点都集中在直线 y = k x y=kx y=kx 上,也可求得方程的积分曲线簇为射线 tan θ = y / x , θ \tanθ=y/x,θ tanθ=y/x,θ为任意常数,原点 O为奇异点。
(2) y ′ = − x / y y'=-x/y y′=−x/y的等斜线为 L k : y = − 1 k x L_k:y=-\frac{1}{k}x Lk:y=−k1x,说明线素斜率为 k 的所有点都集中在直线 y = − 1 k x y=-\frac{1}{k}x y=−k1x 上,且线素斜率和等斜线垂直相交,也可求得方程的积分曲线簇为同心圆 x 2 + y 2 = C 2 x^2+y^2=C^2 x2+y2=C2,原点 O为奇异点。

一阶常微分方程
可分离变量方程
对于形如
d y d x = g ( x ) h ( y ) (1) \frac{\mathrm{d}y}{\mathrm{d}x}=g(x)h(y)\tag{1} dxdy=g(x)h(y)(1)
的微分方程,称为可分离一阶方程(separable first-order equations),方程可化为 1 h ( y ) d y = g ( x ) d x \cfrac{1}{h(y)}\mathrm{d}y=g(x)\mathrm{d}x h(y)1dy=g(x)dx,对方程两边积分
∫ 1 h ( y ) d y = ∫ g ( x ) d x + C \displaystyle\int \cfrac{1}{h(y)}\mathrm{d}y=\int g(x)\mathrm{d}x+C ∫h(y)1dy=∫g(x)dx+C
设 H ( y ) , G ( x ) H(y),G(x) H(y),G(x)分别为 1 h ( y ) , g ( x ) \cfrac{1}{h(y)},g(x) h(y)1,g(x)的原函数,可知隐式通解为 H ( y ) = G ( x ) + C H(y)=G(x)+C H(y)=G(x)+C
这种通过分离变量求方程通解的方法叫做分离变量法(Separation of variables)。
变量替换法
一阶齐次微分方程:可化为
d y d x = φ ( y x ) (1) \frac{\mathrm{d}y}{\mathrm{d}x}=φ(\frac{y}{x})\tag{1} dxdy=φ(xy)(1)
的方程称为一阶齐次微分方程。
引入中间函数 u = y x u=\cfrac{y}{x} u=xy,则 y = u x y=ux y=ux,由此 d y d x = x d u d x + u \dfrac{\mathrm{d}y}{\mathrm{d}x}=x\cfrac{\mathrm{d}u}{\mathrm{d}x}+u dxdy=xdxdu+u
带入原方程 u + x d u d x = φ ( u ) ⟹ d u φ ( u ) − u = d x x u+x\cfrac{\mathrm{d}u}{\mathrm{d}x}=φ(u) \implies \cfrac{\mathrm{d}u}{φ(u)-u}=\cfrac{\mathrm{d}x}{x} u+xdxdu=φ(u)⟹φ(u)−udu=xdx
得到可分离变量的微分方程,求隐式通解即可。
齐次方程等价形式:微分方程
P ( x , y ) d x + Q ( x , y ) d y = 0 (2) P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y=0\tag{2} P(x,y)dx+Q(x,y)dy=0(2)
中的函数 P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P(x,y),Q(x,y)都是 x , y x,y x,y 的同次(例如 k 次)齐次函数,即
P ( t x , t y ) = t k P ( x , y ) , Q ( t x , t y ) = t k Q ( x , y ) P(tx,ty)=t^kP(x,y),Q(tx,ty)=t^kQ(x,y) P(tx,ty)=tkP(x,y),Q(tx,ty)=tkQ(x,y)
比如,线性代数中出现的二次型 f ( x , y ) = a x 2 + b x y + c y 2 f(x, y)=ax^2+bxy+cy^2 f(x,y)=ax2+bxy+cy2 就是一个二次齐次函数,它满足 f ( t x , t y ) = t 2 f ( x , y ) f(tx, ty)=t^2f(x,y) f(tx,ty)=t2f(x,y)
根据齐次函数的定义,我们有 { P ( x , y ) = x k P ( 1 , y / x ) Q ( x , y ) = x k Q ( 1 , y / x ) \begin{cases} P(x,y)=x^kP(1,y/x) \\ Q(x,y)=x^kQ(1,y/x) \\ \end{cases} {P(x,y)=xkP(1,y/x)Q(x,y)=xkQ(1,y/x)
从而方程 (2) 化为下面的形式
x k P ( 1 , y / x ) d x + x k Q ( 1 , y / x ) d y = 0 x^kP(1,y/x)\mathrm{d}x+x^kQ(1,y/x)\mathrm{d}y=0 xkP(1,y/x)dx+xkQ(1,y/x)dy=0
整理可得
d y d x = − P ( 1 , y / x ) Q ( 1 , y / x ) = φ ( y x ) \cfrac{\mathrm{d}y}{\mathrm{d}x}=-\cfrac{P(1,y/x)}{Q(1,y/x)}=φ(\cfrac{y}{x}) dxdy=−Q(1,y/x)P(1,y/x)=φ(xy)
方程化为了齐次方程标准形式,齐次二字来源于齐次函数的定义,所以与齐次线性方程中的齐次不同。
可化为齐次的类型 I
d y d x = f ( a x + b y + c ) (3) \frac{\mathrm{d}y}{\mathrm{d}x}=f(ax+by+c)\tag{3} dxdy=f(ax+by+c)(3)
引入新变量 u = a x + b y + c u=ax+by+c u=ax+by+c ,则 d u d x = a + b d y d x \dfrac{\mathrm{d}u}{\mathrm{d}x}=a+b\dfrac{\mathrm{d}y}{\mathrm{d}x} dxdu=a+bdxdy
带入原方程 d u d x = a + b f ( u ) \dfrac{\mathrm{d}u}{\mathrm{d}x}=a+bf(u) dxdu=a+bf(u)
这是可分离变量的微分方程,求隐式通解即可。
可化为齐次的类型 II
d y d x = f ( a x + b y + c a 1 x + b 1 y + c 1 ) (4) \frac{\mathrm{d}y}{\mathrm{d}x}=f(\frac{ax+by+c}{a_1x+b_1y+c_1})\tag{4} dxdy=f(a1x+b1y+c1ax+by+c)(4)
(1) 当 c = c 1 = 0 c=c_1=0 c=c1=0时,是齐次方程。
(2) 非齐次情形时,令 x = X + h , y = Y + k x=X+h,y=Y+k x=X+h,y=Y+k,于是 d x = d X , d y = d Y \mathrm{d}x=\mathrm{d}X,\mathrm{d}y=\mathrm{d}Y dx=dX,dy=dY,方程化为
d Y d X = f ( a X + b Y + a h + b k + c a 1 X + b 1 Y + a 1 h + b 1 k + c 1 ) \frac{\mathrm{d}Y}{\mathrm{d}X}=f(\frac{aX+bY+ah+bk+c}{a_1X+b_1Y+a_1h+b_1k+c_1}) dXdY=f(a1X+b1Y+a1h+b1k+c1aX+bY+ah+bk+c)
如果方程组
{ a h + b k + c = 0 a 1 h + b 1 k + c 1 = 0 \begin{cases}ah+bk+c=0 \\ a_1h+b_1k+c_1=0\end{cases} {ah+bk+c=0a1h+b1k+c1=0
(i) 系数行列式 ∣ a b a 1 b 1 ∣ ≠ 0 \begin{vmatrix}a&b\\a_1&b_1\end{vmatrix}\neq0 ∣∣∣∣aa1bb1∣∣∣∣=0,即 a 1 a ≠ b 1 b \dfrac{a_1}{a}\neq\dfrac{b_1}{b} aa1=bb1,则可求出 h , k h,k h,k,方程可化为
d Y d X = f ( a X + b Y a 1 X + b 1 Y ) \frac{\mathrm{d}Y}{\mathrm{d}X}=f(\frac{aX+bY}{a_1X+b_1Y}) dXdY=f(a1X+b1YaX+bY)
求出齐次方程的通解后,带入 X = x − h , Y = y − k X=x-h,Y=y-k X=x−h,Y=y−k 即可。
(ii) 当 a 1 a = b 1 b \dfrac{a_1}{a}=\dfrac{b_1}{b} aa1=bb1时,令 a 1 a = b 1 b = λ \dfrac{a_1}{a}=\dfrac{b_1}{b}=λ aa1=bb1=λ,从而
d y d x = f ( a x + b y + c λ ( a x + b y ) + c 1 ) \frac{\mathrm{d}y}{\mathrm{d}x}=f(\frac{ax+by+c}{λ(ax+by)+c_1}) dxdy=f(λ(ax+by)+c1ax+by+c)
引入 v = a x + b y v=ax+by v=ax+by,则 d v d x = a + b d y d x \dfrac{\mathrm{d}v}{\mathrm{d}x}=a+b\dfrac{\mathrm{d}y}{\mathrm{d}x} dxdv=a+bdxdy,方程化为可分离变量的方程
d v d x = a + b f ( v + c λ v + c 1 ) \frac{\mathrm{d}v}{\mathrm{d}x}=a+bf(\frac{v+c}{λ v+c_1}) dxdv=a+bf(λv+c1v+c)
一阶线性微分方程
形如
d y d x + P ( x ) y = Q ( x ) (1) \frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)\tag{1} dxdy+P(x)y=Q(x)(1)
的方程称为一阶线性微分方程(First-order linear differential equation) ,其特点是未知函数 y y y 和它的一阶导数都是一次的。
如果 Q ( x ) ≡ 0 Q(x)\equiv0 Q(x)≡0,称为齐次线性方程, Q ( x ) ≢ 0 Q(x)\not\equiv0 Q(x)≡0,则称为非齐次线性方程。
齐次线性方程:
d y d x + P ( x ) y = 0 (2) \frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=0\tag{2} dxdy+P(x)y=0(2)
是可分离变量的,对方程两边积分得
ln ∣ y ∣ = − ∫ P ( x ) d x + C 1 \ln|y|=-\int P(x)\mathrm{d}x+C_1 ln∣y∣=−∫P(x)dx+C1
或
y = C e − ∫ P ( x ) d x ( C = ± e C 1 ) y=Ce^{-\int P(x)\mathrm{d}x}\quad(C=± e^{C_1}) y=Ce−∫P(x)dx(C=±eC1)
另外 y = 0 y=0 y=0也是方程的特解,称为平凡解。
非齐次线性方程:解非齐次方程 (1) 常用的方法是常数变易法2
(1) 解对应的齐次方程 (2) 通解
(2) 将齐次方程通解中的常数 C C C 换成未知函数 u ( x ) u(x) u(x),做变换
y = u e − ∫ P ( x ) d x (3) \displaystyle y=ue^{-\int P(x)\mathrm{d}x}\tag{3} y=ue−∫P(x)dx(3)
带入方程 (1) 便可求得 u = ∫ Q ( x ) e − ∫ P ( x ) d x d x + C \displaystyle u=\int Q(x)e^{-\int P(x)\mathrm{d}x}\mathrm{d}x+C u=∫Q(x)e−∫P(x)dxdx+C
(3) 将 u 带入方程 (3),便求得非齐次方程的通解
y = e − ∫ P ( x ) d x [ ∫ Q ( x ) e − ∫ P ( x ) d x d x + C ] \displaystyle y=e^{-\int P(x)\mathrm{d}x}[\int Q(x)e^{-\int P(x)\mathrm{d}x}\mathrm{d}x+C] y=e−∫P(x)dx[∫Q(x)e−∫P(x)dxdx+C]
伯努利方程:形如
d y d x + P ( x ) y = Q ( x ) y n \frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)y^n dxdy+P(x)y=Q(x)yn
的微分方程称为伯努利方程(Bernoulli differential equation)
引入变量 u = y 1 − n u=y^{1-n} u=y1−n,方程可转化为一阶线性非齐次方程
d u d x + ( 1 − n ) P ( x ) u = ( 1 − n ) Q ( x ) \dfrac{\mathrm{d}u}{\mathrm{d}x}+(1-n)P(x)u=(1-n)Q(x) dxdu+(1−n)P(x)u=(1−n)Q(x)
可求得通解。
里卡蒂方程:形如
d y d x = P ( x ) y 2 + Q ( x ) y + R ( x ) \cfrac{dy}{dx}=P(x)y^2+Q(x)y+R(x) dxdy=P(x)y2+Q(x)y+R(x)
的微分方程称为 里卡蒂方程 (Riccati equation)。
这是形式上最简单的非线性方程,由十七世纪意大利数学家黎卡提提出来的,在1841年法国数学家刘维尔证明了黎卡提方程一般没有初等解法,即其解不能用初等函数以及初等函数的积分来表示。
但在特殊情况下,是可以求解的。
若已知黎卡提方程的一个特解,则该方程可以求解。
设 y ~ ( x ) \tilde y(x) y~(x) 是方程的一个特解,引入下列变换 y = z + y ~ y=z+\tilde y y=z+y~ 其中 z z z 是新的未知函数,带入方程得到
d y d x = d z d x + d y ~ d x = P ( x ) ( z + y ~ ) 2 + Q ( x ) ( z + y ~ ) + R ( x ) = P ( x ) z 2 + 2 P ( x ) y ~ z + Q ( x ) z + P ( x ) y ~ 2 + Q ( x ) y ~ + R ( x ) \begin{aligned} \cfrac{dy}{dx} &= \cfrac{dz}{dx}+\cfrac{d\tilde y}{dx}=P(x)(z+\tilde y)^2+Q(x)(z+\tilde y)+R(x)\\ &=P(x)z^2+2P(x)\tilde yz+Q(x)z+P(x)\tilde y^2+Q(x)\tilde y+R(x) \end{aligned} dxdy=dxdz+dxdy~=P(x)(z+y~)2+Q(x)(z+y~)+R(x)=P(x)z2+2P(x)y~z+Q(x)z+P(x)y~2+Q(x)y~+R(x)
由于 d y ~ d x = P ( x ) y ~ 2 + Q ( x ) y ~ + R ( x ) \cfrac{d\tilde y}{dx}=P(x)\tilde y^2+Q(x)\tilde y+R(x) dxdy~=P(x)y~2+Q(x)y~+R(x)
可得 d z d x = P ( x ) z 2 + [ 2 P ( x ) y ~ + Q ( x ) ] z \cfrac{dz}{dx}=P(x)z^2+[2P(x)\tilde y+Q(x)]z dxdz=P(x)z2+[2P(x)y~+Q(x)]z
这是以 z z z 为未知函数, n = 2 n=2 n=2 的伯努利方程,是可以求解的。
从而原方程是可以求解的,它的解为: y = z ( x ) + y ~ ( x ) y=z(x)+\tilde y(x) y=z(x)+y~(x)
黎卡提方程告诉我们不是所有的方程都可以用初等积分法来求解的,从而发展起来了新的学科分支微分方程的定性理论。
恰当方程
恰当方程:对称形式的微分方程
P ( x , y ) d x + Q ( x , y ) d y = 0 (1) P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y=0\tag{1} P(x,y)dx+Q(x,y)dy=0(1)
等价于其显示形式 d y d x = − P ( x , y ) Q ( x , y ) = f ( x , y ) \cfrac{\mathrm{d}y}{\mathrm{d}x}=-\cfrac{P(x,y)}{Q(x,y)}=f(x,y) dxdy=−Q(x,y)P(x,y)=f(x,y)
若存在可微函数 F ( x , y ) F(x,y) F(x,y),使得它的全微分为
d F ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y \mathrm{d}F(x,y)=P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y dF(x,y)=P(x,y)dx+Q(x,y)dy
亦即偏导数为
∂ F ∂ x = P ( x , y ) , ∂ F ∂ y = Q ( x , y ) \cfrac{∂F}{∂x}=P(x,y),\quad \cfrac{∂F}{∂y}=Q(x,y) ∂x∂F=P(x,y),∂y∂F=Q(x,y)
则称方程 (1) 为恰当方程 (Exact equation) 或全微分方程。
那么原方程等价于 d F ( x , y ) = 0 \mathrm{d}F(x, y)=0 dF(x,y)=0,即
F ( x , y ) = C F(x,y)=C F(x,y)=C
就是原方程隐式通解, F ( x , y ) F(x,y) F(x,y)称为原函数。
判断恰当方程的充要条件
定理:函数 P ( x , y ) P(x,y) P(x,y) 和 Q ( x , y ) Q(x,y) Q(x,y) 在区域 R : a < x < b , c < y < d R:a
∂ P ∂ y = ∂ Q ∂ x \cfrac{∂P}{∂y}=\cfrac{∂Q}{∂x} ∂y∂P=∂x∂Q
必要性:若 (1) 式为恰当方程,则存在函数 F ( x , y ) F(x,y) F(x,y),满足 ∂ F ∂ x = P ( x , y ) , ∂ F ∂ y = Q ( x , y ) \cfrac{∂F}{∂x}=P(x,y),\cfrac{∂F}{∂y}=Q(x,y) ∂x∂F=P(x,y),∂y∂F=Q(x,y)
则 ∂ P ∂ y = ∂ ∂ y ( ∂ F ∂ x ) = ∂ 2 F ∂ x ∂ y , ∂ Q ∂ x = ∂ ∂ x ( ∂ F ∂ y ) = ∂ 2 F ∂ y ∂ x \cfrac{∂P}{∂y}=\cfrac{∂}{∂y}(\cfrac{∂F}{∂x})=\cfrac{∂^2F}{∂x∂y},\quad \cfrac{∂Q}{∂x}=\cfrac{∂}{∂x}(\cfrac{∂F}{∂y})=\cfrac{∂^2F}{∂y∂x} ∂y∂P=∂y∂(∂x∂F)=∂x∂y∂2F,∂x∂Q=∂x∂(∂y∂F)=∂y∂x∂2F
由P 和Q 具有连续一阶偏导数,可知上述混合偏导数连续且相等,因此必有 ∂ P ∂ y = ∂ Q ∂ y \cfrac{∂P}{∂y}=\cfrac{∂Q}{∂y} ∂y∂P=∂y∂Q
充分性:设函数 P ( x , y ) P(x,y) P(x,y) 和 Q ( x , y ) Q(x,y) Q(x,y)满足条件 ∂ P ∂ y = ∂ Q ∂ x \cfrac{∂P}{∂y}=\cfrac{∂Q}{∂x} ∂y∂P=∂x∂Q
(1) 我们来构造函数 F ( x , y ) F(x, y) F(x,y) 满足 ∂ F ∂ x = P ( x , y ) , ∂ F ∂ y = Q ( x , y ) \cfrac{∂F}{∂x}=P(x,y),\quad \cfrac{∂F}{∂y}=Q(x,y) ∂x∂F=P(x,y),∂y∂F=Q(x,y),首先函数
F ( x , y ) = ∫ P ( x , y ) d x + g ( y ) (2) \displaystyle F(x, y)=\int P(x,y)dx+g(y)\tag{2} F(x,y)=∫P(x,y)dx+g(y)(2)
函数 g ( y ) g(y) g(y)待定,对任意 g ( y ) g(y) g(y) 都满足 ∂ F ∂ x = P ( x , y ) \cfrac{∂F}{∂x}=P(x,y) ∂x∂F=P(x,y)。
(2) 为确定 g ( y ) g(y) g(y),计算第二个偏导数
∂ F ∂ y = ∂ ∂ y ∫ P ( x , y ) d x + g ′ ( y ) = Q \displaystyle \cfrac{∂F}{∂y} =\cfrac{∂}{∂y}\int P(x,y)dx+g'(y)=Q ∂y∂F=∂y∂∫P(x,y)dx+g′(y)=Q
所以 g ′ ( y ) = Q − ∂ ∂ y ∫ P ( x , y ) d x \displaystyle g'(y)=Q-\cfrac{∂}{∂y}\int P(x,y)dx g′(y)=Q−∂y∂∫P(x,y)dx
(3) 为了说明存在这样的函数 g ( y ) g(y) g(y),仅与 y y y 有关,与 x x x 无关,只需证明 g ′ ( y ) g'(y) g′(y) 关于 x 的导数恒为零。根据假设,有
∂ ∂ x [ Q − ∂ ∂ y ∫ P ( x , y ) d x ] = ∂ Q ∂ x − ∂ ∂ x [ ∂ ∂ y ∫ P ( x , y ) d x ] = ∂ Q ∂ x − ∂ ∂ y [ ∂ ∂ x ∫ P ( x , y ) d x ] = ∂ Q ∂ x − ∂ P ∂ y ≡ 0 \begin{aligned} \cfrac{∂}{∂x}\left[Q-\cfrac{∂}{∂y}\int P(x,y)dx\right] &= \cfrac{∂Q}{∂x}-\cfrac{∂}{∂x}\left[\cfrac{∂}{∂y}\int P(x,y)dx\right] \\ &= \cfrac{∂Q}{∂x}-\cfrac{∂}{∂y}\left[\cfrac{∂}{∂x}\int P(x,y)dx\right] \\ &= \cfrac{∂Q}{∂x}- \cfrac{∂P}{∂y} \equiv 0 \end{aligned} ∂x∂[Q−∂y∂∫P(x,y)dx]=∂x∂Q−∂x∂[∂y∂∫P(x,y)dx]=∂x∂Q−∂y∂[∂x∂∫P(x,y)dx]=∂x∂Q−∂y∂P≡0
于是积分可得到 g ( y ) = ∫ [ Q − ∂ ∂ y ∫ P ( x , y ) d x ] d y \displaystyle g(y)=\int \left[Q-\cfrac{∂}{∂y}\int P(x,y)dx\right]dy g(y)=∫[Q−∂y∂∫P(x,y)dx]dy
带入可求得
F ( x , y ) = ∫ P ( x , y ) d x + ∫ [ Q − ∂ ∂ y ∫ P ( x , y ) d x ] d y (3) \displaystyle F(x, y)=\int P(x,y)dx+\int \left[Q-\cfrac{∂}{∂y}\int P(x,y)dx\right]dy\tag{3} F(x,y)=∫P(x,y)dx+∫[Q−∂y∂∫P(x,y)dx]dy(3)
因此满足条件的 (1) 式即为恰当方程,并且隐式通解为
∫ P ( x , y ) d x + ∫ [ Q − ∂ ∂ y ∫ P ( x , y ) d x ] d y = C (4) \displaystyle \int P(x,y)dx+\int \left[Q-\cfrac{∂}{∂y}\int P(x,y)dx\right]dy=C\tag{4} ∫P(x,y)dx+∫[Q−∂y∂∫P(x,y)dx]dy=C(4)
分项凑微分法求解:往往在判断是恰当方程后,并不需要按照上述一般方法来求解,而是采用更简便的分项凑全微分的方法求解,这种方法要求熟记一些简单的全微分。
例如:求解方程 ( 2 x sin y + 3 x 2 y ) d x + ( x 3 + x 2 cos y + 3 y 2 ) d y = 0 (2x\sin y+3x^2y)dx+(x^3+x^2\cos y+3y^2)dy=0 (2xsiny+3x2y)dx+(x3+x2cosy+3y2)dy=0
( 2 x sin y + 3 x 2 y ) d x + ( x 3 + x 2 cos y + 3 y 2 ) d y = ( 2 x sin y d x + x 2 cos y d y ) + ( 3 x 2 y d x + x 3 d y ) + 3 y 2 d y = ( sin y d x 2 + x 2 d sin y ) + ( y d x 3 + x 3 d y ) + 3 y 2 d y = d ( x 2 sin y ) + d ( x 3 y ) + d ( y 3 ) = d ( x 2 sin y + x 3 y + y 3 ) \begin{aligned} & (2x\sin y+3x^2y)dx+(x^3+x^2\cos y+3y^2)dy \\ =& (2x\sin y dx+x^2\cos y dy)+(3x^2ydx+x^3dy)+3y^2dy \\ =&(\sin y dx^2+x^2d\sin y)+(ydx^3+x^3dy)+3y^2dy \\ =&d(x^2\sin y)+d(x^3y)+d(y^3) \\ =&d(x^2\sin y+x^3y+y^3) \end{aligned} ====(2xsiny+3x2y)dx+(x3+x2cosy+3y2)dy(2xsinydx+x2cosydy)+(3x2ydx+x3dy)+3y2dy(sinydx2+x2dsiny)+(ydx3+x3dy)+3y2dyd(x2siny)+d(x3y)+d(y3)d(x2siny+x3y+y3)
所以通解为 x 2 sin y + x 3 y + y 3 = C x^2\sin y+x^3y+y^3=C x2siny+x3y+y3=C
部分全微分
y d x + x d y = d ( x y ) ydx+xdy=d(xy) ydx+xdy=d(xy)
y d x − x d y y 2 = d ( x y ) \cfrac{ydx-xdy}{y^2}=d(\cfrac{x}{y}) y2ydx−xdy=d(yx)
y d x − x d y x y = d ( ln ∣ x y ∣ ) \cfrac{ydx-xdy}{xy}=d(\ln\mid\cfrac{x}{y}\mid) xyydx−xdy=d(ln∣yx∣)
y d x − x d y x 2 + y 2 = d ( arctan x y ) \cfrac{ydx-xdy}{x^2+y^2}=d(\arctan\cfrac{x}{y}) x2+y2ydx−xdy=d(arctanyx)
y d x − x d y x 2 − y 2 = d ( ln ∣ x − y x + y ∣ ) \cfrac{ydx-xdy}{x^2-y^2}=d(\ln\mid\cfrac{x-y}{x+y}\mid) x2−y2ydx−xdy=d(ln∣x+yx−y∣)
− sin ( x + y ) ( d x + d y ) = d cos ( x + y ) -\sin(x+y)(dx+dy)=d\cos(x+y) −sin(x+y)(dx+dy)=dcos(x+y)
cos ( x + y ) ( d x + d y ) = d sin ( x + y ) \cos(x+y)(dx+dy)=d\sin(x+y) cos(x+y)(dx+dy)=dsin(x+y)
积分因子法
对于恰当方程,我们有多种方法求解,比如偏积分法、分项凑微分法等。因此,能否通过一些恒等变形,将非恰当方程化为恰当方程来求解呢?
首先,看一下前面讲的变量分离方程
d y d x = g ( x ) h ( y ) ⟺ g ( x ) h ( y ) d x − d y = 0 \cfrac{\mathrm{d}y}{\mathrm{d}x}=g(x)h(y) \iff g(x)h(y)\mathrm{d}x-\mathrm{d}y=0 dxdy=g(x)h(y)⟺g(x)h(y)dx−dy=0
两端同乘非零函数 μ ( x , y ) = 1 h ( y ) μ(x,y)=\cfrac{1}{h(y)} μ(x,y)=h(y)1 可得恰当方程
g ( x ) d x − 1 h ( y ) d y = 0 g(x)\mathrm{d}x-\cfrac{1}{h(y)}\mathrm{d}y=0 g(x)dx−h(y)1dy=0
然后再看下线性方程
d y d x + P ( x ) y = Q ( x ) ⟺ [ P ( x ) y − Q ( x ) ] d x + d y = 0 \cfrac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x) \iff [P(x)y-Q(x)]\mathrm{d}x+\mathrm{d}y=0 dxdy+P(x)y=Q(x)⟺[P(x)y−Q(x)]dx+dy=0
两端同乘非零函数 μ ( x , y ) = e ∫ P ( x ) d x μ(x,y)=e^{\int P(x)dx} μ(x,y)=e∫P(x)dx 可得恰当方程
M ( x , y ) d x + N ( x , y ) d y = 0 M(x,y)\mathrm{d}x+N(x,y)\mathrm{d}y=0 M(x,y)dx+N(x,y)dy=0
其中
M ( x , y ) = e ∫ P ( x ) d x [ P ( x ) y − Q ( x ) ] , N ( x , y ) = e ∫ P ( x ) d x M(x,y)=e^{\int P(x)dx}[P(x)y-Q(x)] ,N(x,y)=e^{\int P(x)dx} M(x,y)=e∫P(x)dx[P(x)y−Q(x)],N(x,y)=e∫P(x)dx
∂ M ∂ y = P ( x ) e ∫ P ( x ) d x = ∂ N ∂ x \cfrac{∂M}{∂y}=P(x)e^{\int P(x)dx}=\cfrac{∂N}{∂x} ∂y∂M=P(x)e∫P(x)dx=∂x∂N
现在我们尝试将这种方法一般化:对一般的微分方程
P ( x , y ) d x + Q ( x , y ) d y = 0 (1) P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y=0\tag{1} P(x,y)dx+Q(x,y)dy=0(1)
如果存在一个连续可微的非零函数 μ = μ ( x , y ) μ=μ(x,y) μ=μ(x,y),使得
μ P d x + μ Q d y = 0 (2) μP\mathrm{d}x+μQ\mathrm{d}y=0\tag{2} μPdx+μQdy=0(2)
为恰当方程,即 ∂ ( μ P ) ∂ y = ∂ ( μ Q ) ∂ x \frac{∂(μP)}{∂y}=\frac{∂(μQ)}{∂x} ∂y∂(μP)=∂x∂(μQ),则称 μ ( x , y ) μ(x,y) μ(x,y) 为微分方程 (1) 的积分因子(integrating factor)。整理可得积分因子满足方程
Q ∂ μ ∂ x − P ∂ μ ∂ y = ( ∂ P ∂ y − ∂ Q ∂ x ) μ (3) Q\frac{∂μ}{∂x}-P\frac{∂μ}{∂y}=(\frac{∂P}{∂y}-\frac{∂Q}{∂x})μ\tag{3} Q∂x∂μ−P∂y∂μ=(∂y∂P−∂x∂Q)μ(3)
同一方程,可以有不同的积分因子,可以证明,只要方程有解存在,则必有积分因子存在,且不是唯一的。
一般情况下,求解方程 (3) 比求解微分方程 (1) 本身还要难!但是,在某些特殊情形,求解 (3) 还是可以实现的。
-
如果存在一个只与 x x x 有关的积分因子 μ = μ ( x ) μ=μ(x) μ=μ(x) 则 (3) 式变为
Q d μ d x = ( ∂ P ∂ y − ∂ Q ∂ x ) μ Q\frac{dμ}{dx}=(\frac{∂P}{∂y}-\frac{∂Q}{∂x})μ Qdxdμ=(∂y∂P−∂x∂Q)μ
整理可得
1 μ d μ d x = 1 Q ( ∂ P ∂ y − ∂ Q ∂ x ) (4) \frac{1}{μ}\frac{dμ}{dx}=\frac{1}{Q}(\frac{∂P}{∂y}-\frac{∂Q}{∂x})\tag{4} μ1dxdμ=Q1(∂y∂P−∂x∂Q)(4)
它的左端只与 x x x 有关,所以右端亦然,因此,方程 (1) 存在只与 x x x 有关的积分因子的必要条件是:
1 Q ( ∂ P ∂ y − ∂ Q ∂ x ) = G ( x ) (5) \frac{1}{Q}(\frac{∂P}{∂y}-\frac{∂Q}{∂x})=G(x)\tag{5} Q1(∂y∂P−∂x∂Q)=G(x)(5)
只与 x x x 有关。由此可得到积分因子
μ ( x ) = e ∫ G ( x ) d x (6) μ(x)=e^{\int G(x)dx}\tag{6} μ(x)=e∫G(x)dx(6)定理 1:微分方程 (1) 存在仅依赖于 x x x 的积分因子的充要条件是表达式 (5) 只与 x x x 有关,而与 y y y 无关。而且函数 (6) 就是一个积分因子。
类似的,我们得到下面的平行结果。
定理 2:微分方程 (1) 存在仅依赖于 y y y 的积分因子的充要条件是表达式 1 P ( ∂ Q ∂ x − ∂ P ∂ y ) = H ( y ) \displaystyle\frac{1}{P}(\frac{∂Q}{∂x}-\frac{∂P}{∂y})=H(y) P1(∂x∂Q−∂y∂P)=H(y) 只与 y y y 有关,而与 x x x 无关。而且函数 μ ( y ) = e ∫ H ( y ) d y μ(y)=e^{\int H(y)dy} μ(y)=e∫H(y)dy 就是一个积分因子。 -
分组求积分因子
定理 3:若 μ = μ ( x , y ) μ=μ(x,y) μ=μ(x,y) 是微分方程 (1) 的一个积分因子,使得
μ P ( x , y ) d x + μ Q ( x , y ) d y = d Φ ( x , y ) μP(x,y)dx+μQ(x,y)dy=dΦ(x,y) μP(x,y)dx+μQ(x,y)dy=dΦ(x,y)
则 μ ( x , y ) g [ Φ ( x , y ) ] μ(x,y)g[Φ(x,y)] μ(x,y)g[Φ(x,y)] 也是微分方程 (1)的一个积分因子,其中 g ( ⋅ ) g(\cdot) g(⋅)是任意可微的(非零)函数。下面是对分组求积分因子的一般化说法。
假设微分方程 (1) 的左端可以分成两组,即
( P 1 d x + Q 1 d y ) + ( P 2 d x + Q 2 d y ) = 0 (P_1dx+Q_1dy)+(P_2dx+Q_2dy)=0 (P1dx+Q1dy)+(P2dx+Q2dy)=0
其中第一组和第二组各有积分因子 μ 1 , μ 2 μ_1,μ_2 μ1,μ2 使得
μ 1 ( P 1 d x + Q 1 d y ) = d Φ 1 , μ 2 ( P 2 d x + Q 2 d y ) = d Φ 2 μ_1(P_1dx+Q_1dy)=dΦ_1,\quad μ_2(P_2dx+Q_2dy)=dΦ_2 μ1(P1dx+Q1dy)=dΦ1,μ2(P2dx+Q2dy)=dΦ2
由定理3可知,对任意可微函数 g 1 , g 2 g_1,g_2 g1,g2,函数 μ 1 g 1 ( Φ 1 ) , μ 2 g 2 ( Φ 2 ) μ_1g_1(Φ_1),μ_2g_2(Φ_2) μ1g1(Φ1),μ2g2(Φ2) 分别为第一、第二组的积分因子。因此,如果能适当选取 g 1 , g 2 g_1,g_2 g1,g2,使得 μ 1 g 1 ( Φ 1 ) = μ 2 g 2 ( Φ 2 ) μ_1g_1(Φ_1)=μ_2g_2(Φ_2) μ1g1(Φ1)=μ2g2(Φ2) ,则 μ = μ 1 g 1 ( Φ 1 ) μ=μ_1g_1(Φ_1) μ=μ1g1(Φ1) 就是微分方程 (1)的积分因子。
例如,求解微分方程 ( x 3 y − 2 y 2 ) d x + x 4 d y = 0 (x^3y-2y^2)dx+x^4dy=0 (x3y−2y2)dx+x4dy=0
将方程左端分组 ( x 3 y d x + x 4 d y ) − 2 y 2 d x = 0 (x^3ydx+x^4dy)-2y^2dx=0 (x3ydx+x4dy)−2y2dx=0
前一组有积分因子 x − 3 x^{-3} x−3 和通积分 x y = C xy=C xy=C;后一组有积分因子 y − 2 y^{-2} y−2 和通积分 y = C y=C y=C
我们要寻找可微函数 g 1 , g 2 g_1,g_2 g1,g2,使得 x − 3 g 1 ( x , y ) = y − 2 g 2 ( x ) x^{-3}g_1(x,y)=y^{-2}g_2(x) x−3g1(x,y)=y−2g2(x)
只要取 g 1 ( x , y ) = 1 ( x y ) 2 , g 2 ( x ) = 1 x 5 g_1(x,y)=\cfrac{1}{(xy)^2}, g_2(x)=\cfrac{1}{x^5} g1(x,y)=(xy)21,g2(x)=x51
从而的到原方程得积分因子 μ = 1 x 5 y 2 μ=\cfrac{1}{x^5y^2} μ=x5y21
即可化为全微分方程 1 ( x y ) 2 d ( x y ) − 2 x 5 d x = 0 \cfrac{1}{(xy)^2}d(xy)-\cfrac{2}{x^5}dx=0 (xy)21d(xy)−x52dx=0
积分此式,不难得到原方程通解 y = 2 x 3 2 C x 4 + 1 y=\cfrac{2x^3}{2Cx^4+1} y=2Cx4+12x3,外加特解 x = 0 , y = 0 x=0,y=0 x=0,y=0 。他们实际上是用积分因子乘方程时丢失的解。
等角轨线族
假设在 ( x , y ) (x,y) (x,y) 平面上由方程
Φ ( x , y , C ) = 0 (1) Φ(x,y,C)=0\tag{1} Φ(x,y,C)=0(1)
给出一个以C为参数的曲线族,我们设法求出另一个曲线族
Ψ ( x , y , K ) = 0 (2) Ψ(x,y,K)=0\tag{2} Ψ(x,y,K)=0(2)
其中K为参数,使得曲线族(2)中的任一条曲线与曲线族(1)中的每一条曲线相交成定角 α ( − π 2 < α ⩽ π 2 ) α (-\cfrac{π}{2}<α⩽\cfrac{π}{2}) α(−2π<α⩽2π),以逆时针方向为正,则称这样的曲线族(2)为已知曲线族(1)的 等角轨线族(family of isogonal trajectories),特别,当 α = π 2 α=\cfrac{π}{2} α=2π时,称曲线族(2)为(1)的正交轨线族(family of orthogonal trajectories)。
方程(1)是一个单参数的曲线族,可以先求出它的每一条曲线满足的微分方程,再利用等角轨线的几何解释,得出等角轨线满足的微分方程,然后解此方程,即得所求的等角轨线族(2)。
具体来说,假设偏导 Φ C ≠ 0 Φ_C\neq0 ΦC=0,则可联立方程
{ Φ ( x , y , C ) = 0 Φ x ( x , y , C ) d x + Φ y ( x , y , C ) d y = 0 (3) \begin{cases} Φ(x,y,C)=0 \\ Φ_x(x,y,C)dx+Φ_y(x,y,C)dy=0 \end{cases} \tag{3} {Φ(x,y,C)=0Φx(x,y,C)dx+Φy(x,y,C)dy=0(3)
消去C,得到曲线族满足的微分方程
d y d x = H ( x , y ) (4) \cfrac{dy}{dx}=H(x,y)\tag{4} dxdy=H(x,y)(4)
其中 H ( x , y ) = − Φ x [ x , y , C ( x , y ) ] Φ y [ x , y , C ( x , y ) ] H(x,y)=-\cfrac{Φ_x[x,y,C(x,y)]}{Φ_y[x,y,C(x,y)]} H(x,y)=−Φy[x,y,C(x,y)]Φx[x,y,C(x,y)],这里 C = C ( x , y ) C=C(x,y) C=C(x,y) 是由 Φ ( x , y , C ) = 0 Φ(x,y,C)=0 Φ(x,y,C)=0 决定的函数。
如果我们把方程(4)在点 ( x , y ) (x,y) (x,y) 的线素斜率记为 y 1 ′ y'_1 y1′,而把与它相交成角 α α α的线素斜率记为 y ′ y' y′ ,则
(1) 当 α ≠ π 2 α\neq\cfrac{π}{2} α=2π时,有 tan α = y ′ − y 1 ′ 1 + y ′ y 1 ′ \tan α=\cfrac{y'-y'_1}{1+y'y'_1} tanα=1+y′y1′y′−y1′ ,即 y 1 ′ = y ′ − tan α 1 + y ′ tan α y'_1=\cfrac{y'-\tan α}{1+y'\tan α} y1′=1+y′tanαy′−tanα
因为 y 1 ′ = H ( x , y ) y'_1=H(x,y) y1′=H(x,y) ,所以等角轨线的微分方程为 H ( x , y ) = y ′ − tan α 1 + y ′ tan α H(x,y)=\cfrac{y'-\tan α}{1+y'\tan α} H(x,y)=1+y′tanαy′−tanα 即
d y d x = H ( x , y ) + tan α 1 − H ( x , y ) tan α \cfrac{dy}{dx}=\cfrac{H(x,y)+\tan α}{1-H(x,y)\tan α} dxdy=1−H(x,y)tanαH(x,y)+tanα
(2) 而当 α = π 2 α=\cfrac{π}{2} α=2π时,就有 y ′ = − 1 y 1 ′ y'=-\cfrac{1}{y'_1} y′=−y1′1 ,亦即可得正交轨线的微分方程为
d y d x = − 1 H ( x , y ) \cfrac{dy}{dx}=-\cfrac{1}{H(x,y)} dxdy=−H(x,y)1
求解微分方程就可得到等角轨线族(正交轨线族)。
等角轨线族不仅在数学中有用,例如当 0 < α < π 0<α<π 0<α<π 时,可取为坐标系。而且在某些物理和力学中也有用,例如静电场中电场线和等势线互为正交轨线族。
一阶隐式微分方程
一阶隐式微分方程(First-order implicit differential equation) 的一般形式为
F ( x , y , d y d x ) = 0 F(x,y,\frac{dy}{dx})=0 F(x,y,dxdy)=0
所谓隐式的含义是指在方程中未知函数的导数 d y d x \frac{dy}{dx} dxdy没有表示成 ( x , y ) (x, y) (x,y) 的显函数。求解一阶隐式方程主要有两种方法:微分法和参数法,这两种方法的目的就是把隐式方程表示成显式方程来求解。
微分法:它主要针对 y y y 被解出的方程( x x x 被解出的方程同理)
y = f ( x , p ) y=f(x,p) y=f(x,p)
其中 p = d y d x p=\cfrac{dy}{dx} p=dxdy,即 d y = p d x dy=pdx dy=pdx
假设函数 f ( x , p ) f(x, p) f(x,p) 对 ( x , p ) (x, p) (x,p) 是连续可微的, 那么对上式微分,便得到
d y = ∂ f ∂ x ( x , p ) d x + ∂ f ∂ p ( x , p ) d p dy=\cfrac{∂f}{∂x}(x,p)dx+\cfrac{∂f}{∂p}(x,p)dp dy=∂x∂f(x,p)dx+∂p∂f(x,p)dp
从而得到关于 x , p x, p x,p 的一阶显式微分方程
[ ∂ f ∂ x ( x , p ) − p ] d x + ∂ f ∂ p ( x , p ) d p = 0 [\cfrac{∂f}{∂x}(x,p)-p]dx+\cfrac{∂f}{∂p}(x,p)dp=0 [∂x∂f(x,p)−p]dx+∂p∂f(x,p)dp=0
求解方程可能出现以下情形:
(1) p = φ ( x , C ) p=φ(x,C) p=φ(x,C) ,便得到通解 y = f ( x , φ ( x , C ) ) y=f(x,φ(x,C)) y=f(x,φ(x,C)),这是最理想的结果
(2) x = φ ( p , C ) x=φ(p,C) x=φ(p,C) ,得参数方程表示的解 { x = φ ( p , C ) y = f ( φ ( x , C ) , p ) \begin{cases} x=φ(p,C) \\ y=f(φ(x,C),p) \end{cases} {x=φ(p,C)y=f(φ(x,C),p)
(3) 若得到关系式 Φ ( x , p , C ) = 0 Φ(x,p,C)=0 Φ(x,p,C)=0 ,原方程的解只好表示为 { Φ ( x , p , C ) = 0 y = f ( x , p ) \begin{cases} Φ(x,p,C)=0 \\ y=f(x,p) \end{cases} {Φ(x,p,C)=0y=f(x,p)
参数法:对于不明显包含自变量的方程
F ( y , p ) = 0 F(y, p)=0 F(y,p)=0
其中 p = d y d x p=\cfrac{dy}{dx} p=dxdy
由于函数 F ( y , p ) = 0 F(y, p)=0 F(y,p)=0 表示平面 y O p yOp yOp 平面一条曲线或若干条曲线,而曲线都可以用参数方程表示,所以我们下面引入参数
{ y = g ( t ) p = h ( t ) \begin{cases} y=g(t) \\ p=h(t) \end{cases} {y=g(t)p=h(t) ,带入 p = d y d x p=\cfrac{dy}{dx} p=dxdy 可得 d x = g ′ ( t ) h ( t ) d t dx=\cfrac{g'(t)}{h(t)}dt dx=h(t)g′(t)dt
显然是可分离变量方程,可直接积分得到通解
{ x = ∫ g ′ ( t ) h ( t ) d t + C y = g ( t ) \begin{cases} \displaystyle x=\int\cfrac{g'(t)}{h(t)}dt +C \\ y=g(t) \end{cases} ⎩⎨⎧x=∫h(t)g′(t)dt+Cy=g(t)
参数法对于方程 F ( x , p ) = 0 F(x, p)=0 F(x,p)=0 同样适用。
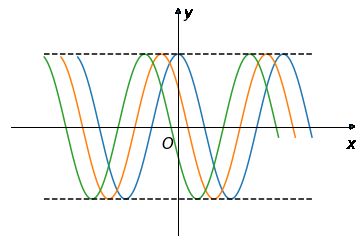
示例:求解微分方程 y 2 + ( d y d x ) 2 = 1 y^2+(\cfrac{dy}{dx})^2=1 y2+(dxdy)2=1
显然,方程有参数表达式 { y = cos t d y d x = sin t ( − ∞ < t < + ∞ ) \begin{cases} y=\cos t \\ \cfrac{dy}{dx}=\sin t \end{cases} (-∞
由此可得, d x = ( cos t ) ′ sin t − d t dx=\cfrac{(\cos t)'}{\sin t}-dt dx=sint(cost)′−dt
从而求得 x = − t + C x=-t+C x=−t+C,又因 y = cos t y=\cos t y=cost
可得通解为 y = cos ( C − x ) y=\cos(C-x) y=cos(C−x)
除了上述参数形式的解外,还可设 { y = ± 1 d y d x = 0 \begin{cases} y=\pm1 \\ \cfrac{dy}{dx}=0 \end{cases} ⎩⎨⎧y=±1dxdy=0
可知 y ± 1 y\pm1 y±1也是方程的特解。积分曲线簇见下图:
对于一般的一阶隐式微分方程
F ( x , y , p ) = 0 ( p = d y d x ) F(x,y,p)=0\quad (p=\frac{dy}{dx}) F(x,y,p)=0(p=dxdy)
在 x , y , p x,y,p x,y,p 空间表示曲面,设它的参数方程为 { x = f ( u , v ) y = g ( u , v ) p = h ( u , v ) \begin{cases} x=f(u,v) \\ y=g(u,v) \\ p=h(u,v) \end{cases} ⎩⎪⎨⎪⎧x=f(u,v)y=g(u,v)p=h(u,v)
因为 d y = p d x dy=pdx dy=pdx ,所以我们有
g u d u + g v d v = h ( u , v ) ( f u d u + f v d v ) g_udu+g_vdv=h(u,v)(f_udu+f_vdv) gudu+gvdv=h(u,v)(fudu+fvdv)
可以写成如下形式
M ( u , v ) d u + N ( u , v ) d v = 0 M(u,v)du+N(u,v)dv=0 M(u,v)du+N(u,v)dv=0
其中 { M ( u , v ) = g u ( u , v ) − h ( u , v ) f u ( u , v ) M ( u , v ) = g v ( u , v ) − h ( u , v ) f v ( u , v ) \begin{cases} M(u,v)=g_u(u,v)-h(u,v)f_u(u,v) \\ M(u,v)=g_v(u,v)-h(u,v)f_v(u,v) \end{cases} {M(u,v)=gu(u,v)−h(u,v)fu(u,v)M(u,v)=gv(u,v)−h(u,v)fv(u,v)
如果我们能求得上述一阶显式方程的通解
v = Q ( u , C ) v=Q(u,C) v=Q(u,C)
则微分方程有通解 { x = f [ u , Q ( u , C ) ] y = g [ u , Q ( u , C ) ] \begin{cases} x=f[u,Q(u,C)] \\ y=g[u,Q(u,C)] \end{cases} {x=f[u,Q(u,C)]y=g[u,Q(u,C)]
另外,如果显式方程除通解外,还有特解 v = S ( u ) v=S(u) v=S(u)
则微分方程有特解 { x = f [ u , S ( u ) ] y = g [ u , S ( u ) ] \begin{cases} x=f[u,S(u)] \\ y=g[u,S(u)] \end{cases} {x=f[u,S(u)]y=g[u,S(u)]
解的存在和唯一性定理
里卡蒂方程的例子说明还有大量的方程的解不能用初等解法来求出通解的。而实际问题中所需要的往往是满足某种初始条件得解。因此对初值问题的研究被提到了重要的地位。自然要问,初值问题的解是否存在?若存在,是否唯一呢?
解的存在和唯一性定理
(1) 首先考虑导数已求出的一阶显式微分方程初值问题
{ d y d x = f ( x , y ) y ( x 0 ) = y 0 (E) \begin{cases} \cfrac{dy}{dx}=f(x,y)\\ y(x_0)=y_0 \end{cases}\tag{E} ⎩⎨⎧dxdy=f(x,y)y(x0)=y0(E)
利普希茨条件:存在常数 L > 0 L>0 L>0 ,使得函数 f ( x , y ) f(x,y) f(x,y)在区域D内满足不等式
∣ f ( x , y 1 ) − f ( x , y 2 ) ∣ ⩽ L ∣ y 1 − y 2 ∣ |f(x,y_1)-f(x,y_2)|⩽L|y_1-y_2| ∣f(x,y1)−f(x,y2)∣⩽L∣y1−y2∣
则称函数 f ( x , y ) f(x,y) f(x,y)在区域D内对 y y y 满足利普希茨条件(Lipschitz condition), L L L 称为利普希茨常数。
定理 1:皮卡定理(Picard theorem) ,如果函数 f ( x , y ) f(x,y) f(x,y) 在矩形区域
R : ∣ x − x 0 ∣ ⩽ a , ∣ y − y 0 ∣ ⩽ b R:|x-x_0|⩽a, |y-y_0|⩽b R:∣x−x0∣⩽a,∣y−y0∣⩽b
内连续,且关于 y y y 满足利普希茨条件,则初值问题 ( E ) (E) (E)在区间 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h存在唯一解。其中常数
h = min { a , b M } , M = max ( x , y ) ∈ R ∣ f ( x , y ) ∣ h=\min\{a,\cfrac{b}{M}\},\displaystyle M=\max_{(x,y)\in R}|f(x,y)| h=min{a,Mb},M=(x,y)∈Rmax∣f(x,y)∣
我们采用皮卡(Picard)的逐步逼近法来证明这个定理。

-
命题 1 设 y = φ ( x ) y=φ(x) y=φ(x) 是初值问题
{ d y d x = f ( x , y ) ( 1.1 ) φ ( x 0 ) = y 0 ( 1.2 ) (E) \begin{cases} \cfrac{dy}{dx}=f(x,y)\quad &(1.1)\\ φ(x_0)=y_0\quad &(1.2) \end{cases}\tag{E} ⎩⎨⎧dxdy=f(x,y)φ(x0)=y0(1.1)(1.2)(E)
的解的充要条件是 y = φ ( x ) y=φ(x) y=φ(x) 是积分方程
y = y 0 + ∫ x 0 x f ( x , y ) d x ( 1.3 ) y=y_0+\int_{x_0}^xf(x,y)dx\quad(1.3) y=y0+∫x0xf(x,y)dx(1.3)
的连续解。
证明:因为 y = φ ( x ) y=φ(x) y=φ(x)是方程 (1.1) 的解,故有
d φ ( x ) d x ≡ f ( x , φ ( x ) ) \cfrac{dφ(x)}{dx}\equiv f(x,φ(x)) dxdφ(x)≡f(x,φ(x))两边从 x 0 x_0 x0到 x x x取定积分,有
φ ( x ) − φ ( x 0 ) ≡ ∫ x 0 x f ( x , φ ( x ) ) d x φ(x)-φ(x_0)\equiv \int_{x_0}^xf(x,φ(x))dx φ(x)−φ(x0)≡∫x0xf(x,φ(x))dx由于 φ ( x 0 ) = y 0 φ(x_0)=y_0 φ(x0)=y0 ,带入可得
φ ( x ) = y 0 + ∫ x 0 x f ( x , φ ( x ) ) d x φ(x)=y_0+\int_{x_0}^xf(x,φ(x))dx φ(x)=y0+∫x0xf(x,φ(x))dx因此 y = φ ( x ) y=φ(x) y=φ(x)是积分方程 (1.3) 的连续解。
反之,只要设 y = φ ( x ) y=φ(x) y=φ(x)是积分方程 (1.3) 的连续解,逆转上面的推导,就可得到 y = φ ( x ) y=φ(x) y=φ(x)是初值问题(E)的解。 -
逐次迭代法构建皮卡序列(Picard sequence)
任取一个连续函数 φ 0 ( x ) φ_0(x) φ0(x) 带入积分方程(1.3)右端的 y y y,就得到函数
φ 1 ( x ) = y 0 + ∫ x 0 x f ( x , φ 0 ( x ) ) d x φ_1(x)=y_0+\int_{x_0}^xf(x,φ_0(x))dx φ1(x)=y0+∫x0xf(x,φ0(x))dx
显然 φ 1 ( x ) φ_1(x) φ1(x)也是连续函数,如果 φ 1 ( x ) ≡ φ 0 ( x ) φ_1(x)\equiv φ_0(x) φ1(x)≡φ0(x) ,那么 φ 0 ( x ) φ_0(x) φ0(x)就是积分方程(1.3)的解(解的定义);否则,我们又把 φ 1 ( x ) φ_1(x) φ1(x)带入积分方程(1.3)的右端的 y y y,得到
φ 2 ( x ) = y 0 + ∫ x 0 x f ( x , φ 1 ( x ) ) d x φ_2(x)=y_0+\int_{x_0}^xf(x,φ_1(x))dx φ2(x)=y0+∫x0xf(x,φ1(x))dx
如果 φ 2 ( x ) ≡ φ 1 ( x ) φ_2(x)\equiv φ_1(x) φ2(x)≡φ1(x) ,那么 φ 1 ( x ) φ_1(x) φ1(x)就是积分方程(1.3)的解;否则,我们继续这个步骤。一般的,我们作函数
φ n ( x ) = y 0 + ∫ x 0 x f ( x , φ n − 1 ( x ) ) d x φ_n(x)=y_0+\int_{x_0}^xf(x,φ_{n-1}(x))dx φn(x)=y0+∫x0xf(x,φn−1(x))dx
这样,就得到连续函数序列 φ 0 ( x ) , φ 1 ( x ) , ⋯ , φ n ( x ) φ_0(x),φ_1(x),\cdots,φ_n(x) φ0(x),φ1(x),⋯,φn(x)
如果 φ n + 1 ( x ) ≡ φ n ( x ) φ_{n+1}(x)\equiv φ_n(x) φn+1(x)≡φn(x) ,那么 φ n ( x ) φ_n(x) φn(x)就是积分方程(1.3)的解。 -
命题 2 取 φ 0 ( x ) = y 0 φ_0(x)=y_0 φ0(x)=y0,构造皮卡序列
{ φ 0 ( x ) = y 0 φ n ( x ) = y 0 + ∫ x 0 x f ( x , φ n − 1 ( x ) ) d x ( n = 1 , 2 , ⋯ ) (1.4) \begin{cases} φ_0(x)=y_0 \\ \displaystyleφ_n(x)=y_0+\int_{x_0}^xf(x,φ_{n-1}(x))dx\quad(n=1,2,\cdots) \end{cases}\tag{1.4} ⎩⎨⎧φ0(x)=y0φn(x)=y0+∫x0xf(x,φn−1(x))dx(n=1,2,⋯)(1.4)
序列中所有的函数 φ n ( x ) φ_n(x) φn(x) 在区间 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h 上有定义、连续,且满足不等式
∣ φ n ( x ) − y 0 ∣ ⩽ b |φ_n(x)-y_0|⩽b ∣φn(x)−y0∣⩽b
证明:用数学归纳法
当 n = 1 n=1 n=1 时, φ 1 ( x ) = y 0 + ∫ x 0 x f ( ξ , y 0 ) d ξ \displaystyleφ_1(x)=y_0+\int_{x_0}^xf(ξ,y_0)dξ φ1(x)=y0+∫x0xf(ξ,y0)dξ,显然 φ 1 ( x ) φ_1(x) φ1(x)在 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h 上有定义、连续且有
∣ φ 1 ( x ) − y 0 ∣ = ∣ ∫ x 0 x f ( ξ , y 0 ) d ξ ∣ ⩽ ∫ x 0 x ∣ f ( ξ , y 0 ) ∣ d ξ ⩽ M ∣ x − x 0 ∣ ⩽ M h ⩽ b \displaystyle|φ_1(x)-y_0|=|\int_{x_0}^xf(ξ,y_0)dξ|⩽\int_{x_0}^x|f(ξ,y_0)|dξ \\ ⩽M|x-x_0|⩽Mh⩽b ∣φ1(x)−y0∣=∣∫x0xf(ξ,y0)dξ∣⩽∫x0x∣f(ξ,y0)∣dξ⩽M∣x−x0∣⩽Mh⩽b
即当 n = 1 n=1 n=1 时,命题2 成立。
现在用数学归纳法证明对于任何正整数 n ,命题2都成立。
假设当 n = k n=k n=k时, φ k ( x ) φ_k(x) φk(x)在 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h 上有定义、连续且有
∣ φ k ( x ) − y 0 ∣ ⩽ b |φ_k(x)-y_0|⩽b ∣φk(x)−y0∣⩽b
这时, φ k + 1 ( x ) = y 0 + ∫ x 0 x f ( x , φ k ( x ) ) d x \displaystyleφ_{k+1}(x)=y_0+\int_{x_0}^xf(x,φ_k(x))dx φk+1(x)=y0+∫x0xf(x,φk(x))dx在 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h 上有定义、连续,且
∣ φ k + 1 ( x ) − y 0 ∣ ⩽ ∫ x 0 x ∣ f ( ξ , φ k ( x ) ) ∣ d ξ ⩽ M ∣ x − x 0 ∣ ⩽ M h ⩽ b \displaystyle|φ_{k+1}(x)-y_0|⩽\int_{x_0}^x|f(ξ,φ_k(x))|dξ ⩽M|x-x_0|⩽Mh⩽b ∣φk+1(x)−y0∣⩽∫x0x∣f(ξ,φk(x))∣dξ⩽M∣x−x0∣⩽Mh⩽b
即命题2在 n = k + 1 n=k+1 n=k+1时也成立。
由数学归纳法得知命题2对于所有 n 均成立。
- 命题 3 皮卡序列 { φ n ( x ) } \{φ_n(x)\} {φn(x)} 在 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h上是一致收敛的。
证明:我们考虑级数
φ 0 ( x ) + ∑ k = 1 ∞ [ φ k ( x ) − φ k − 1 ( x ) ] (1.5) \displaystyle φ_0(x)+\sum_{k=1}^{\infty}[φ_k(x)-φ_{k-1}(x)]\tag{1.5} φ0(x)+k=1∑∞[φk(x)−φk−1(x)](1.5)
它的部分和为
φ 0 ( x ) + ∑ k = 1 n [ φ k ( x ) − φ k − 1 ( x ) ] = φ n ( x ) \displaystyle φ_0(x)+\sum_{k=1}^{n}[φ_k(x)-φ_{k-1}(x)]=φ_n(x) φ0(x)+k=1∑n[φk(x)−φk−1(x)]=φn(x)
因此,要证明 { φ n ( x ) } \{φ_n(x)\} {φn(x)}在 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h上一致收敛,只需证明级数(1.5)在 ∣ x − x 0 ∣ ⩽ h |x-x_0|⩽h ∣x−x0∣⩽h上一致收敛。
为此,我们进行如下估计:
∣ φ 1 ( x ) − φ 0 ( x ) ∣ ⩽ ∫ x 0 x ∣ f ( ξ , φ 0 ( ξ ) ) ∣ d ξ ⩽ M ∣ x − x 0 ∣ \displaystyle|φ_1(x)-φ_0(x)|⩽\int_{x_0}^x|f(ξ,φ_0(ξ))|dξ ⩽M|x-x_0| ∣φ1(x)−φ0(x)∣⩽∫x0x∣f(ξ,φ0(ξ))∣dξ⩽M∣x−x0∣
由(1.4)及李普希兹条件,我们有
∣ φ 2 ( x ) − φ 1 ( x ) ∣ ⩽ ∫ x 0 x ∣ f ( ξ , φ 1 ( ξ ) ) − f ( ξ , φ 0 ( ξ ) ) ∣ d ξ ⩽ L ∫ x 0 x ∣ φ 1