Leetcode-第十一题Container With Most Water

题目链接

https://leetcode.com/problems/container-with-most-water/

题目

Given n non-negative integers a1, a2, …, an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

题意理解和解答

很明显，第一种是蛮力算法，O(n^2）

class Solution {//返回最大容积，这个求的时间复杂度是O(n^2)
public:
    int maxArea(vector<int>& height) {
        int n=height.size();
        int max_v=0;
        int temp=0;
        for(int i=0;i1;i++)
        {
            for(int j=i+1;jif(temp>max_v)
                    max_v=temp;
            }
        }
        return max_v;
    }
private:
int min(int a,int b)
{
    if(a>b) return b;
    else return a;
}
};

无需解释，也通不过，时间复杂度过高。

下面从网上找的一种O(N)的算法，着实精妙！

思路：
用两个指针分别指向a1到an的头和尾，然后计算a1和an围成的面积，之后比较height[i]和height[j]，如果height[i]小，就把i指针向前移动i++，如果j小，就把j指针向前移动，j–，重新计算新的height[i]和height[j]组成的面积，直到i和j相遇，比较这n个面积的最大值，就是所要求的。

为哈？

哈哈，开始我也想了好久，看了网上的解答好久，终于想明白了这事。
下面用h[i]来表示height[i]。

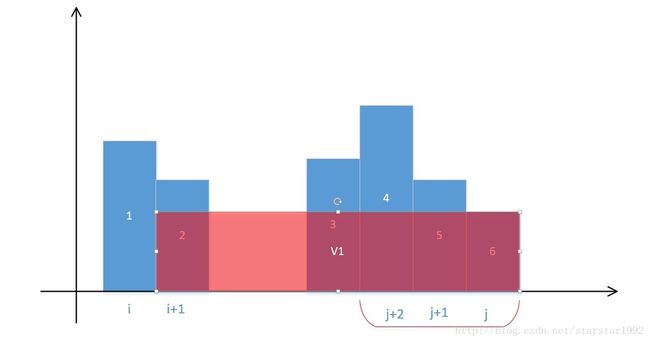
自己想想想，这个算法能把n*(n-1)次计算面积简化成n次计算面积，一下子省略了这么多，肯定有窍门。
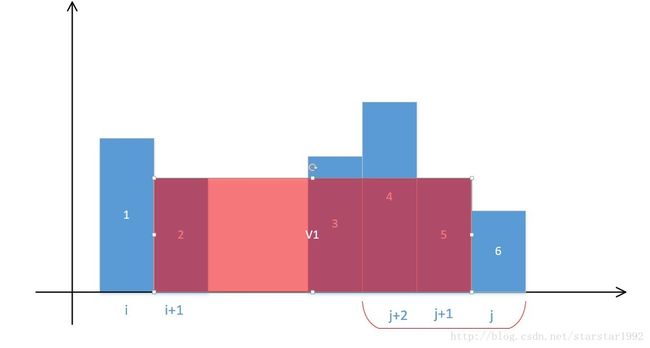
先看上图，假设某一次移动后如上。那么此时计算1和6组成的容器，很明显是下图：

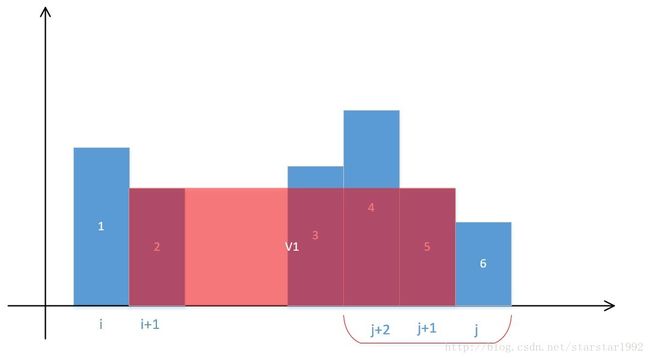
之后比较h[i]和h[j]，可以看出j应该–，跑到j+1位置处。
然后计算新的面积：

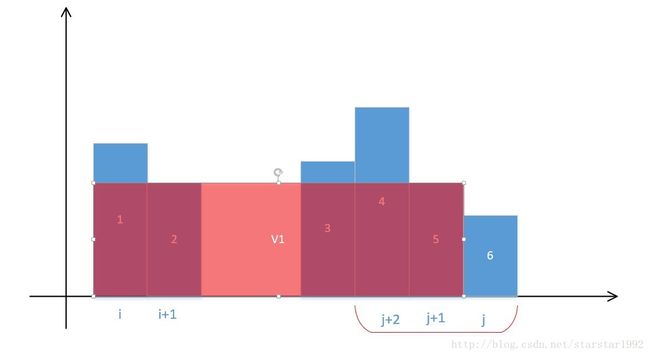
之后再次比较h[i]和h[j]，j还–，跑到j+2处。
然后计算新的面积：

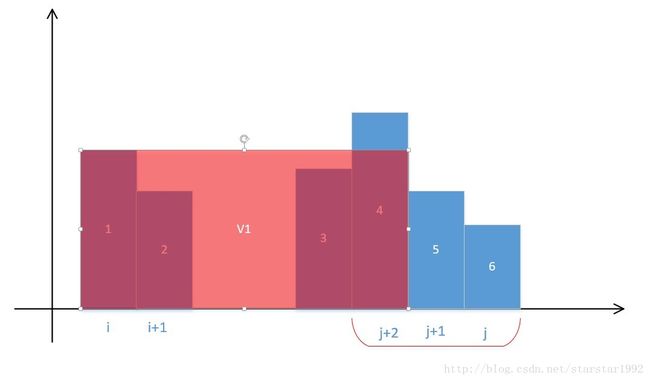
之后再次比较h[i]和h[j]，i++，跑到i+1处。
然后计算新的面积：

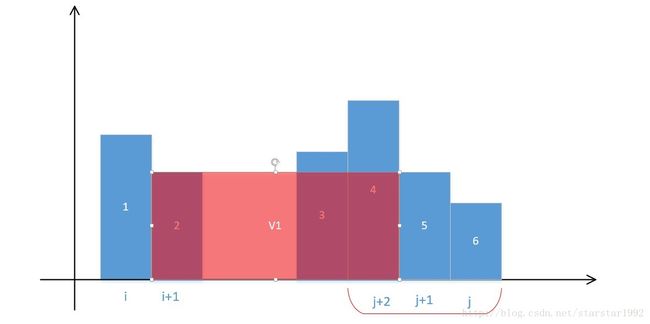
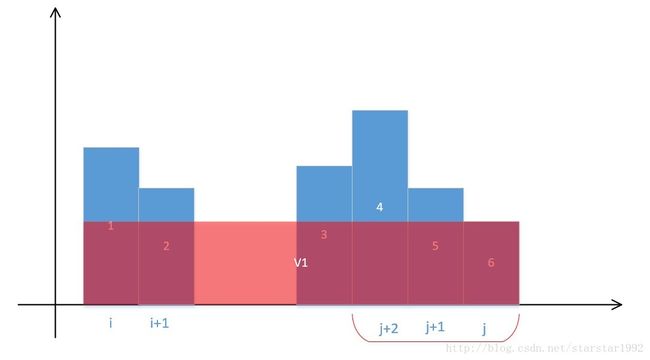
这样我们可以一直比较下去计算面积，但是到这一步，先停下来想想，i从i到i+1，j从j到j+2，总共有6个组合，即（i,j），(i+1,j)，(i,j+1)，(i+1,j+1)，(i,j+2)，(i+1,j+2)。按照蛮力算法，应该计算6次面积，但是上面我们只计算了4次，省略了两次，现在再看看省略的两次：如下

2和6组成的面积

2和5组成的面积

仔细想想，省略的这两次有没有可能是这6次中最大的。答案：不可能

因为2和6的组合肯定没有1和6的组合大！
2和5的组合肯定没有1和5的组合大！（1高于2）
所以可以省略这两次比较。

现在我们只是比较了左边的两块和右边的三块，当把i增多，j也增多，就可以省略更多，这个需要慢慢体会。

所以上面提出的算法是可以理解的。

AC代码

class Solution {
public:
    int maxArea(vector<int>& height)
    {
        int max_c=0;
        int len=height.size();
        int i=0,j=len-1;
        int container=0;
        while(true)
        {
            if(i==j)
                break;
            container=(j-i)*min(height[i],height[j]);
            if(container>max_c)
                max_c=container;
            if(height[i]else
                j--;
        }
        return max_c;
    }
private:
    int min(int a,int b)
    {
        if(areturn a;
        else return b;
    }
};