神经网络算法详解 04:反馈神经网络(Hopfield、BAM、BM、RBM)
本文介绍了反馈神经网络,包括Hopfield网络,离散Hopfield网络(DHNN),连续Hopfield网络(CHNN),双向联想记忆网络(BAM),玻尔兹曼机(BM),受限玻尔兹曼机(RBM)。其中对于BAM、BM、RBM只是对其进行了简单的介绍,并没有详细地推导算法。本文的目的旨在了解这些算法,先知道这些网络的改进和应用场景,当有业务需求的时候,再详细研究。
系列文章:
- 【神经网络算法详解 01】-- 人工神经网络基础
- 【神经网络算法详解 02】 – 感知神经网络与反向传播算法(BP)
- 【神经网络算法详解 03】 – 竞争神经网络【SONN、SOFM、LVQ、CPN、ART】
- 【神经网络算法详解 04】 – 反馈神经网络 【Hopfield、DHNN、CHNN、BAM、BM、RBM】
- 【神经网络算法详解 05】-- 其它类型的神经网络简介【RBF NN、DNN、CNN、LSTM、RNN、AE、DBN、GAN】
文章目录
- 系列文章:
- 1. 反馈神经网络
- 1.1 知识回顾:前馈神经网络
- 1.2 反馈与前馈神经网络的区别
- 2. Hopfield 网
- 3. 离散Hopfield网络(DHNN)
- 3.1 DHNN的特点
- 3.2 DHNN网络状态
- 3.3 能量函数
- 3.4 DHNN的工作方式
- 3.5 DHNN例子
- 3.6 DHNN网络容量
- 3.7 DHNN 设计权重和阈值
- 3.7.1 联立方程组法
- 3.7.2 外积法
- 3.8 DHNN简单应用案例:OCR字符识别
- 4. 连续Hopfield网络
- 4.1 CHNN网络结构
- 4.2 CHNN网络拓扑
- 4.3 CHNN几个特点
- 4.4 CHNN应用的几个步骤
- 4.5 TSP 问题
- 5. 双向联想记忆神经网络(BAM)
- 5.1 网络运行过程
- 5.2 能量函数与权值设计
- 5.3 网络特点
- 6. 玻尔兹曼机(BM)
- 6.1 模拟退火算法
- 6.2 BM的能量函数
- 6.3 BM的特点
- 6.4 自联想与异联想
- 6.5 受限玻尔兹曼机
1. 反馈神经网络
1.1 知识回顾:前馈神经网络
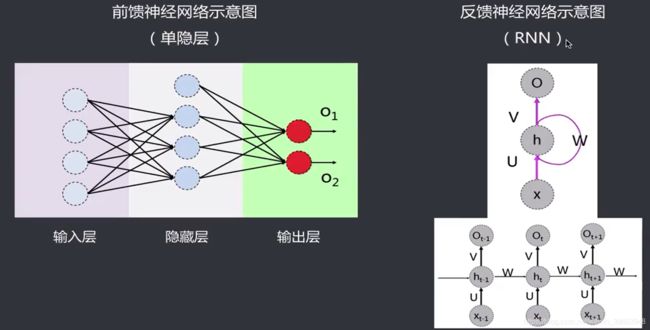
前馈神经网络(FeedForwardNN):是一种最简单的神经网络,采用单向多层结构各神经元分层排列,每个神经元只与前一层的神经元相连。接收前一层的输出并输出给下一层各层间没有反馈。
前馈网络包括三类节点·
- 输入节点(lnputNodes):外界信息输入,不进行任何计篇,仅向下一层节点传递信息
- 的藏节点(HiddenNodes):接收上一层节点的输入,进行计算,并将信息传到下一层节点
- 输出节点(OutputNodes):接收上一层节点的输入,进行计算,并将结果输出
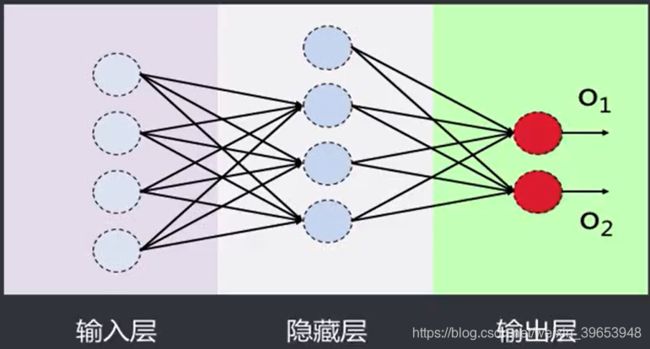
输入层和输出层须有,隐藏层可以没有,即为单层感知器藏层也可以不止一层,有藏层的前馈网络即多层感知器。
1.2 反馈与前馈神经网络的区别
反馈神经网络(FeedBackNN):又称递归网络、回归网络,是一种将输出经过一步时移再接入到输入层的神经网络系统。这类网络中,神经元可以互连,有些神经元的输出会被反馈至同层甚至前层的神经元。常见的有Hopfield神经网络、Elman神经网络、Boltzmann机等。
前馈神经网络和反馈神经网络的主要区别:
- 前馈神经网络各层神经元之间无连接,神经元只接受上层传来的数据,处理后传入下一层,数据正向流动;反馈神经网络层间神经元有连接,数据可以在同层间流动或反馈至前层。
- 前馈神经网络不考虑输出与输入在时间上的滞后效应只表达输出与输入的映射关系;反馈神经网络考虑输出与输入之间在时间上的延迟,需要动态方程来描述系统的模型。
- 前馈神经网络的学习主要采用误差修止法(如BP算法),计算过程一般比较慢,收敛速度也比较慢;反馈神经网络主要采用Hebb学习规则,一般情况下计算的收敛速度很快。
- 相比前馈神经网络,反馈神经网络更适合应用在联想记忆和优化计算等领域。
2. Hopfield 网
【 HopfieId网】是一种单层对称全反馈网络,1982年由加州理工学院的物理学家上J. J.HopfieId 提出,因此被称作HopfieId网。他在该反馈网络中引入了“能量函数”,即认为该网络为一种基于能量的的模型(Energy Based Model,EBM)。能量函数的提出意义重大,它保证了向局部极小的收敛,使神经网络运行稳定性的判断有了明确的可靠的依据。Hopfield网提供了模拟人类记忆的模型。1985年的时候还和D.W.Tank一块模拟电子线路实现了Hopfield网络,并用此解决了旅行商TSP问题。
- 根据激活函数不同,分为两种:离散HopfieId网(Discrete Hopfield Neural Network,DHNN)和连续 Hopfield网(Continuous Hopfield Neural Network,CHNN);
- DHNN主要用于联想记忆,输入部分信息即可联想到完整的输出,即具有容错性;
- CHNN主要用于优化计算,如旅行商TSP、调度等。
3. 离散Hopfield网络(DHNN)
3.1 DHNN的特点
- 单层、全连接、反馈:任一神经元输出 x i x_i xi 均通过权重 w i j w_{ij} wij反馈至所有神经元 x j x_j xj作为输入,即让任一神经元的输出都能受到所有神经元的控制,从而使袢经元的输出能互相制约。
- 每个神经元均有一个阈值 T j T_j Tj,以反映对输入噪声的控制。DHHN网的关踺因素为权重矩阵及神经元阈值,因此也可以简单记作: N = ( W , T ) N=(W,T) N=(W,T)。
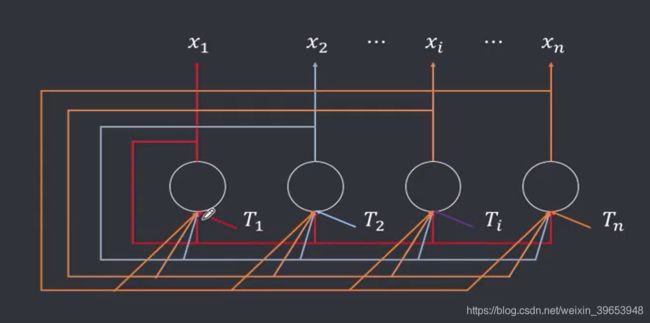
网络系统具有若干个稳定状态,当网络从某一初始状态开始运动,网络系统总可以收敛于一个稳定状态。
系统稳定的平衡状态可以通过设计网络的权值而被存储到网络中。简单的来讲就是,Hopfield网络的主要功能是联想记忆。既然如此,首先应该让网络实现“记忆”,我们需要一些数据,然后训练网络,训完练完成之后,可以的得到一组可用的权值信息,形成网络的“记忆”功能。,当输入数据不完整时,根据训练得到的权重去运算,得到一个稳定的输出状态,这就是联想功能。
3.2 DHNN网络状态
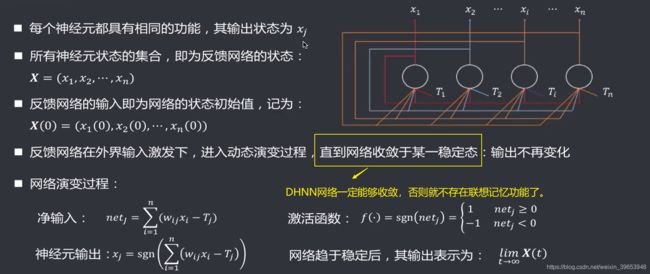
DHHN反馈网络实质上能存储若干个预先设置的稳定状态的网络,运行时外界提供一个输入作为初始网络状态,网络将该输入对应的输出反馈回来作为下次的输入,经过多次循环迭代后,在某些条件下,网络会最终稳定在某一个预先设定好的定点。稳态使得DHHN具有联想记忆功能。
网络稳定性:网络从初态 X ( 0 ) X(0) X(0) 开始,经过有限次递归后,其状态不再发生变化,即 X ( t + 1 ) = X ( t ) X(t+1)=X(t) X(t+1)=X(t),则称该网络是稳定的。
3.3 能量函数
能量函数用来表征系统的稳定性,在满足一定的条件下,某种“能量函数”的能量在网络运行过程中不断减小,当能量最终定于一个常数时,网络趋于最终的稳定态。
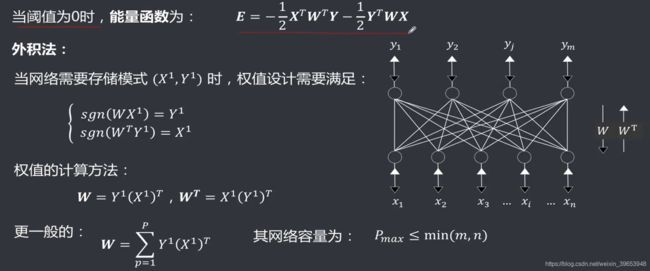
E ( t ) = − 1 2 X T ( t ) W X ( t ) + X T ( t ) T E(t) = - \frac{1}{2} X^T(t)WX(t) + X^T(t)T E(t)=−21XT(t)WX(t)+XT(t)T
利用网络的能量数可实现优化求解功能。网络的能量函数在网络状态按一定规则变化时,能自动趋向能量的极小点。如果把一个待求解问题的目标函数以网络能量函数的形式表达出来,当能量函数趋于最小时,对应的网络状态就是问题的最优解。网络的初态可视为问题的初始解,而网络从初态向稳态的收敛过程便是优化计算的过程,这种寻优搜索是在网络演变过程中自动完成的。
网络达到稳定时的状态 X X X称为网络的吸引子。若把需记忆的样本信息存储于网络的不同吸引子,当输入含有部分记忆信息的样本时网络的演变过程就是便是从部分信息寻找全部信息即联想回忆的过程。
3.4 DHNN的工作方式
3.5 DHNN例子
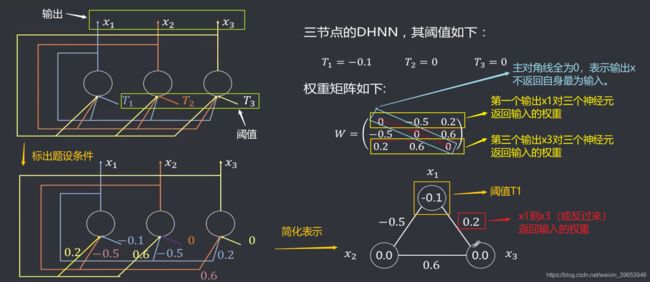
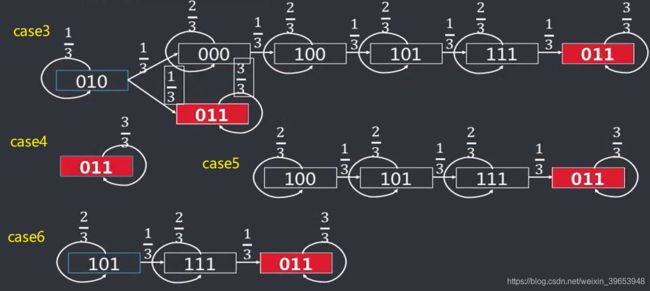
三节点的DHNN网络,其阈值、权重值都已经确定,即该网络能够存储的记忆值均以确定。按照异步工作模式,计算网络的演变过程。
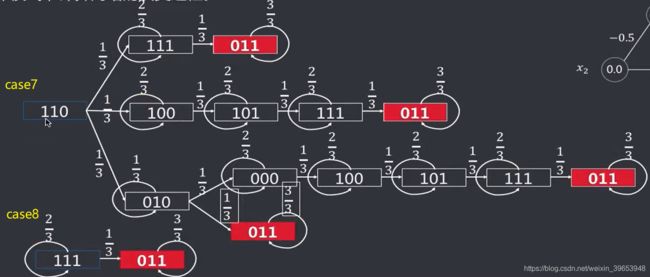
经过以上分析,有3个节点的输入状态,共有八种( 2 3 2^3 23)初始状态的可能情况。
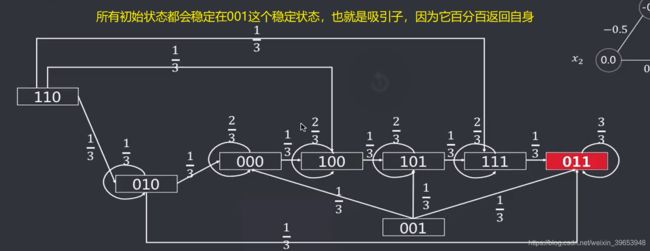
3.6 DHNN网络容量
DHNN网络容量:简单理解为DHNN网络可以准确记住的模式个数。当其规模为 n n n,且权重阵的对角线元素为0,那么该网络的容量的上界为ne实际上由于多种原因,很难达到上界。
让网络准确记住一个模式比较容易,但在记忆模式个数增加时,会出现以下两种情况:
- 权值侈动:当网络记住第一个模式后,在记忆第二模式的时候,会导致原来的矩阵发生变化,有可能会导致对之前模式的“遗忘”。下式中通Hebb规则进行权重更新,当K值较小时,可以将输入样本变为吸引子;当K值较大时,不但难以成为吸引子,而且很可能影响之前的吸引子,引发对之前样本的遗忘,称作“疲劳”。
W = W + X K ( X K ) T − 1 W = W + X^K(X^K)^T - 1 W=W+XK(XK)T−1 - 交叉干扰:当网络学习多个样本后,在回忆阶段即验证记忆样本时,所产生的干扰成为交叉干扰。如果记忆模式之间并非正交的话,记忆容量会严重下降。
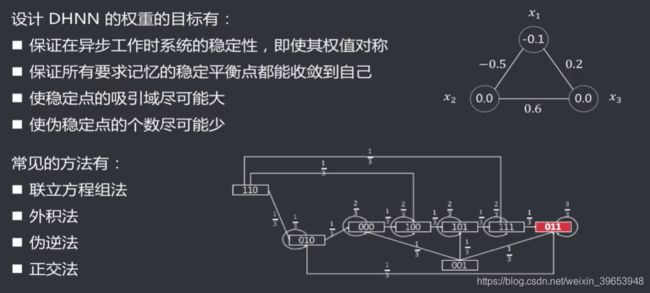
3.7 DHNN 设计权重和阈值
3.7.1 联立方程组法
联立方程组法:通过预先设定的吸引子,列出联立方程组,求解方程组,确定每个权值和阈值的取值范围,找任一组符合上述范围要求的值即可。

得到约束方程组:

求解思路:

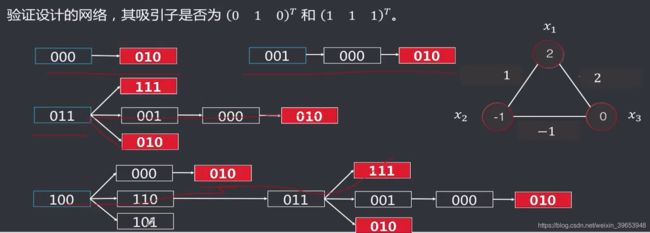
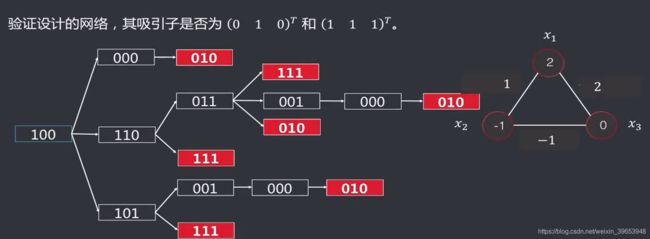
经过以上推导可知,满足吸引子,所以是满足条件的解。但是当节点数量增多时则不适用(指数级上升, 2 N , N 为 节 点 数 2^N,N为节点数 2N,N为节点数),因此提出了外积法。
3.7.2 外积法
外积法:通过Hebb规则,确定网络的权重(包括阈值)。该方法更通用,并且可以处理节点比较多的情况。

实例:

3.8 DHNN简单应用案例:OCR字符识别
通过DHNN联想记忆功能,预先建立DHNN网络模型,将需要识别的字符(信息),通过网络的权重和阈值保存到网络中。应用于识别有噪声的字符。
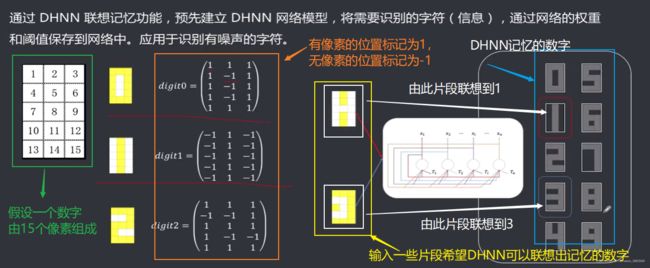
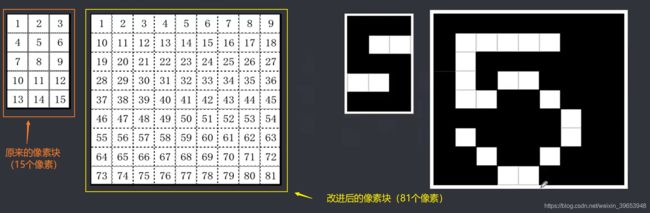
以上识别效果不好,进行改进:
思路:增加像素数目,即将原来5×3的像素块,变为9×9的像素块,这样,网络“记忆”的信息就多了,识别也更准确。
4. 连续Hopfield网络
CHNN&DHNN的主要区别:
- 输入输出不同:DHNN输入输出都是离散值,CHNN输入输出都是连续的模拟量;
- 激活函数不同:DHNN的激活函数为符号函数,CHNN激活函数支持多种,包括线性函数、非线性函数(sigmoid)等;
- 工作方式不同:DHNN支持同步或者异步,CHNN主要是同步工作。
4.1 CHNN网络结构
- CHNN中所有神经元都随时间t并行更新,网络状态随时间连续变化;
- CHNN模型可与电子线路对应,每一个神经元可用一个运算放大器来模拟;
- 神经元的输入与输出分别用运算放大器的输入电压 u i u_i ui和输出电压 v i v_i vi表示;
- 连接权 w i j w_{ij} wij用输入端的电导表示
- 每个神经元有一个用于设置活电平的外界输入偏置电流,相当于阈值
- c i c_i ci和 1 g i \frac{1}{g_i} gi1上分别为运放的等效输入电容和电阻,模拟生物神经元的输出时间常数。
4.2 CHNN网络拓扑
4.3 CHNN几个特点
- 具有良好的收敛性;
- 具有有限个平衡点;
- 如果平衡点稳定,则网络是渐进稳定的;
- 渐进稳定平衡点是网络能量函数的局部极小点;
- 能将任意一组希望存储的正交化矢量综合为网络的渐进平衡点;
- 网络的存储信息表现为神经元之间互相连接的分布式动态存储;
- 网络以大规模、非线性、并行的方式进行信息处理;
4.4 CHNN应用的几个步骤
应用CHNN解决实际问题,通畅由以下步骤组成:
- 对于给定问题,要选择一种合适的表示方法,使得神经网络的输出与问题的解相对应;
- 构造网络能量函数,使其最小值对应于问题的最佳解;
- 将构造的能量函数和标准能量函数的方程比较,可推出神经网络的权值与偏流的表达式,从而确定网络结构;
- 构建网络后,其稳态就是在一定条件下的问题优化解,可以通过电路或者计算机模拟求解。
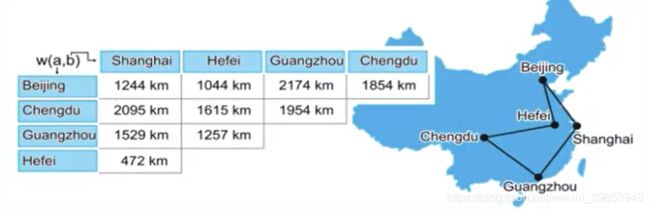
4.5 TSP 问题
- 从某个城市出发,最后回到该城市
- 每个城市只能访问一次
- 所走路程最近
当有3个城市:有 1 1 1 种方法
当有5个城市:有 12 12 12 种方法
当有7个城市:有 360 360 360 种方法
当有10个城市:有 181440 181440 181440 种方法
当有15个城市:有生 4.36 × 1 0 10 4.36\times10^{10} 4.36×1010 种方法
当有20个城市有: 2.43 × 1 0 19 2.43 \times 10^{19} 2.43×1019 种方法
当有31个城市有: 1.27 × 1 0 35 1.27×10^{35} 1.27×1035 种方法
5. 双向联想记忆神经网络(BAM)
- 双层双向网络
- 信息可以双向传播
- 状态输出为单极性二进制{1,0},或者双极性离散值{1,一1}
- 不同方向的输入,使用的权重矩阵互为转置 W W W 和 W T W^T WT。
5.1 网络运行过程
5.2 能量函数与权值设计
5.3 网络特点
1.网络设计比较简单
- 只需要几组输入和几组典型输出
- 权值由输入输出简单计算得到
- 运行时由实际输出与权向量矩阵做内积计算得到相应的输出
2.大规模并行处理,可以处理较大的数据量
3.实时性和容错性较好
4.无需对输入向量进行预处理,可直接输入,不需要编码和解码
6. 玻尔兹曼机(BM)

玻尔兹曼机〈Bolt zmann Machine):也称Stochastic Hopfield Network with Hidden Units,是一种随机递归神经网络,可以看做是一种随机生成的HopfieId网络。1983年-1986年,由Hinton和Sejnowski提出,该神经网络只有0和1两种状态,其取值根据规律统计法则决定,其形式与注明的统计力学家
BoItzmann提出的分布相似,因此被称为BoItzmann机。
- 有可见节点和藏节点之分;
- 形式上和单层反馈网络DHNN非韋接近;
- 可见节点实现输入输出,隐藏节点实现输入输出间的联系;
- 从功能上看,和三层BP网络比较接近;
- 权重矩阵对称,且自反馈为0,即 w i j = w j i w_{ij}=w_{ji} wij=wji且 w i i = 0 w_{ii}=0 wii=0。
6.1 模拟退火算法
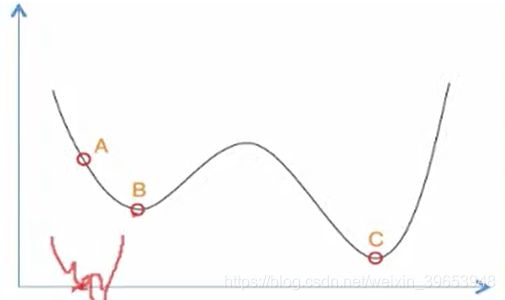
【模拟退火算法(SimulatedAnneal)】:所谓退火是指物体温度逐渐降低的现象,随着温度降低,物体的能量状态会低,在结晶状态时能量最低。模拟退火算法也是模拟退火的过程,但是它在搜索过程中加入了随机因素:即在达到最优值(可能是局部最优值)后会以一定的概率跳出来。如右图,当搜索到局部最优值B后,会按照某个概率继续向右移动,使得搜索有可能跳出局部最优值,而去获得下一个最优值(可能是局部最优也可能是全局最优)。
6.2 BM的能量函数
6.3 BM的特点
6.4 自联想与异联想
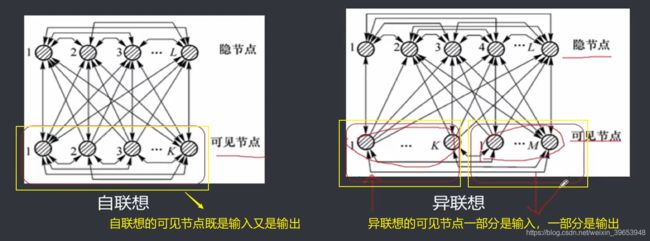
自联想的输出节点和输出节点相同,即可见节点既是输入节点又是输出节点;异联想的输出节点
和输入节点不同,即部分可见节点为输入节点,其余可见节点为输出节点。
通过有导师学习,BM可以对训练集中各模式的概率分布进行模拟,从而实现联想记忆。学习的
目的是通过调整网络权值使训练集中的模式在网络状态中以相同的概率再现。
-
到第一阶段:正向学习
向网络输入一对输入一输出模式,将网络的输入一输出节点限制到期望的状态,即固定住输入输出的状态,而去自由调整隐藏层,以完成输入输出之间的映射。 -
第二阶段:反向学习
对于异联想学习,用输入模式固定输入节点,而让输出和隐藏节点自由活动;对于自联想学习让可见节点和隐藏节点都自由活动,以体现输入一输出对应规律的模拟情况。输入一输出的对应规律表现为网络达到热平衡时,相连节点状态同时为1的概率。期望对应规律与模拟对应规律之间的差别就表现为两个学习阶段所对应的平均概率的差值,基于该值去调节权重。
6.5 受限玻尔兹曼机
受限玻尔兹曼机(Restricted Boltzmann Machine,RBM),是一种简化的特殊的玻尔兹曼机,1986年由Paul Smolensky提出。和BM比,其隐藏层中的节点之间没有互相连接,其可见节点间也没有连接,因此其计算相对更简单。RBM可以应用于降维、分类、协同过滤、特征学习和主题建模等领域,根据任务的不同,可以选择监督学习或者非监督学习等方式进行神经网络模型训练。
- 到两层结构:可见层和隐藏层
- 同层内无连接,不同层全连接:同层内节点激活状态独立
- 节点状态二值状态:0 和 1
- 计算相对BM简单
- 只要隐层节点足够多,能拟合任何离散分布
课程链接:https://edu.aliyun.com/course/1923