5/5
又是三题滚粗了,注定是打铁的命~~
题A Alyona and Numbers
题意:给你n和m,找[1, n]和[1,m]范围内的两个数相加,有多少个的和是5的倍数?
题解:枚举x在[1,n]的范围,然后得到范围[x + 1, x + m]的数,求有多少个是5的倍数即可。
1 /*zhen hao*/
2 #include
3 using namespace std;
4
5 #define lson l, m, rt*2
6 #define rson m + 1, r, rt*2+1
7 #define xx first
8 #define yy second
9
10 typedef pair<int,int> pii;
11 typedef long long ll;
12 typedef unsigned long long ull;
13
14 int main() {
15 // freopen("case.in", "r", stdin);
16 int n, m;
17 ll res = 0;
18 cin >> n >> m;
19 for (int i = 1; i <= n; i++) {
20 int l = i + 1, r = i + m;
21 res += (r / 5) - ((l - 1) / 5);
22 }
23 cout << res << endl;
24 return 0;
25 }
题B Alyona and Mex
题意:给你n个数,让你可以对任意一个数变成小于它的数,然后问你最后这个序列的最小的没有的正整数是多少?
题解:水题,排个序,然后扫一下即可。
1 /*zhen hao*/
2 #include
3 using namespace std;
4
5 #define lson l, m, rt*2
6 #define rson m + 1, r, rt*2+1
7 #define xx first
8 #define yy second
9
10 typedef pair<int,int> pii;
11 typedef long long ll;
12 typedef unsigned long long ull;
13
14 const int maxn = 1e5 + 100;
15 int v[maxn];
16
17 int main() {
18 // freopen("case.in", "r", stdin);
19 int n;
20 cin >> n;
21 for (int i = 0; i < n; i++) {
22 scanf("%d", v + i);
23 }
24 sort(v, v + n);
25 int c = 0;
26 for (int i = 0; i < n; i++) {
27 if (v[i] > c) c++;
28 }
29 cout << c + 1 << endl;
30 return 0;
31 }
题C Alyona and the Tree
题意:给你n个带权点,然后组成一棵带权树,然后对于一个点u,如果存在子树中的点v使得dist(u,v) > av,那么这个点为sad点,问你删除最少多少个点使得这棵树没有sad点?
题解:一开始想麻烦了,O(n ^ 2)肯定超时,开始的想法是对于这个点的子树中有多少个不是sad点,然后传上去继续判断,这样就中了出题人的圈套。应该分析的是这个v,而不是u,也就是说对于v的祖先是固定的,这么多祖先中有没有使得自己变sad点的,也就是存不存在u使得满足dist(u,v) > av,av是固定的,也就是说我们去路径的最大值看一下满不满足,如果最大值都不满足的话,那么一定都可以,这个点就一定不是sad点,标记一下,最后再dfs一下统计个数即可。
1 /*zhen hao*/
2 #include
3 using namespace std;
4
5 #define lson l, m, rt*2
6 #define rson m + 1, r, rt*2+1
7 #define xx first
8 #define yy second
9
10 typedef pair<int,int> pii;
11 typedef long long ll;
12 typedef unsigned long long ull;
13
14 const int maxn = 1e5 + 100;
15 int a[maxn], e, head[maxn], flag[maxn];
16
17 struct Edge {
18 int v, w, nx;
19 } edges[maxn * 2];
20
21 void init() {
22 e = 0;
23 memset(head, -1, sizeof head);
24 }
25
26 void add_edge(int u, int v, int w) {
27 edges[e] = (Edge){v, w, head[u]};
28 head[u] = e++;
29 }
30
31 void dfs1(int u, int p, ll d) {
32 for (int i = head[u]; ~i; i = edges[i].nx) {
33 int v = edges[i].v;
34 if (v == p) continue;
35 if (d + edges[i].w > a[v] || edges[i].w > a[v]) flag[v] = 1;
36 else dfs1(v, u, max((ll)edges[i].w, d + edges[i].w));
37 }
38 }
39
40 int dfs2(int u, int p) {
41 if (flag[u]) return 0;
42 int ret = 1;
43 for (int i = head[u]; ~i; i = edges[i].nx) {
44 int v = edges[i].v;
45 if (v == p) continue;
46 ret += dfs2(v, u);
47 }
48 return ret;
49 }
50
51 int main() {
52 // freopen("case.in", "r", stdin);
53 int n;
54 cin >> n;
55 for (int i = 1; i <= n; i++) {
56 scanf("%d", a + i);
57 }
58 init();
59 for (int i = 2; i <= n; i++) {
60 int u, w;
61 scanf("%d%d", &u, &w);
62 add_edge(i, u, w);
63 add_edge(u, i, w);
64 }
65 dfs1(1, -1, 0);
66 cout << n - dfs2(1, -1) << endl;
67 return 0;
68 }
题D Alyona and Strings
题意:给你两个串,然后你可以分割s出k个子串,然后这k个子串在t串中出现,且顺序一样,问你这k个串最长是多少?
题解:这题是到水题,由于比赛没时间做,真是可惜了~~。正解是dp,dp(i,j,k)表示s的i,t的j,分割出了k各部分,然后最长是多少?有一个问题,就是想要接着上一个串继续组成k个部分要满足上一个串的最后两个刚好是i-1和j-1,所以这里要再加一维l,0表示最长,1表示以当且字符串结尾的最长,最后转移一下就好了。我觉得可行的还有一种解法就是pres和pret表示匹配的对应的s和t的最后两个位置,也是一样的效果,懒得写了!!
1 /*zhen hao*/
2 #include
3 using namespace std;
4
5 const int L = 1100, K = 11;
6 int dp[L][L][K][2];
7 char s[L], t[L];
8
9 int main() {
10 // freopen("case.in", "r", stdin);
11 int n, m, k;
12 cin >> n >> m >> k >> s >> t;
13
14 for (int i = 1; i <= n; i++)
15 for (int j = 1; j <= m; j++)
16 for (int l = 1; l <= k; l++) {
17 if (s[i - 1] == t[j - 1]) {
18 dp[i][j][l][1] = 1 + max(dp[i - 1][j - 1][l][1], dp[i - 1][j - 1][l - 1][0]);
19 }
20 dp[i][j][l][0] = max(dp[i][j][l][1], max(dp[i - 1][j][l][0], dp[i][j - 1][l][0]));
21 }
22
23 cout << dp[n][m][k][0] << endl;
24 return 0;
25 }
题E Alyona and Triangles
题意:给你n个点和一个面积S,然后让你构造一个三角形,满足这个三角形包围了所有的点,并且面积不大于4S,输出满足的任意三个点即可。
题解:这道题是计算几何,一直没怎么做过计算几何的题目,暑假要好好补一补才行了。
这道题是凸包+旋转卡壳。
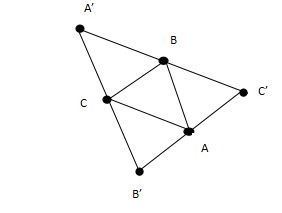
首先直接抛出这道题的做法:先从这n个点找出三个点使得所有组成的三角形中面积最大,然后构造一个三角形的所有边的中点为刚才求出的三角形的点,就像下图(其中ABC就是求出来的,A’B’C’就是扩大之后的):
接下来证明一下为什么可以这么做:
(1)先证明这个A’B’C’三角形的面积是不会超过4S的。
假设这个ABC的面积是s,由题目得s <= S,然后由初中的几何性质可知BC//B’C’,AB//A’B’,AC//A’C’;然后我们可知ABA’C是一个平行四边形,所以角A等于角A’,根据面积公式S = a * b * sinC / 2.0所以面积变为原来面积的4倍,刚好是4s<=4S;
(2)接下来证明为什么这个大三角形包括了所有凸包上的点,假设有个点D跑出去了,很容易证这个ABD、ACD、BCD至少有一个三角形的面积是大于ABC的,这与ABC就是三个点构成三角形最大的矛盾了,所以一定可以包括这个凸包的所有点。
最后讲一下怎么找这个ABC?
这是个经典题目
这个题目的做法要用到类似用旋转卡壳找最远点对(凸包的直径)的做法。具体就是固定两个相邻点i和j,然后找最远的k,然后固定k移动j,然后k就随着j进行移动(O(n)),然后枚举所有的i点,所以复杂度就是O(n ^ 2)。
1 /*zhen hao*/
2 #include
3 using namespace std;
4
5 typedef long long ll;
6 const int maxn = 5e4 + 100;
7
8 struct Point {
9 ll x, y;
10 bool operator < (const Point& o) const {
11 return x < o.x || (x == o.x && y < o.y);
12 }
13 Point operator - (const Point& o) const {
14 return (Point){x - o.x, y - o.y};
15 }
16 bool operator == (const Point& o) const {
17 return x == o.x && y == o.y;
18 }
19 } p[maxn], ch[maxn];
20
21 ll cross(Point A, Point B) {
22 return A.x * B.y - A.y * B.x;
23 }
24
25 int convex_hull(int n) {
26 sort(p, p + n);
27 n = unique(p, p + n) - p;
28 int m = 0;
29 for (int i = 0; i < n; i++) {
30 while (m > 1 && cross(ch[m - 1] - ch[m - 2], p[i] - ch[m - 2]) <= 0) --m;
31 ch[m++] = p[i];
32 }
33 int k = m;
34 for (int i = n - 2; i >= 0; i--) {
35 while (m > k && cross(ch[m - 1] - ch[m - 2], p[i] - ch[m - 2]) <= 0) --m;
36 ch[m++] = p[i];
37 }
38 if (n > 1) --m;
39 return m;
40 }
41
42 int resi, resj, resk;
43
44 void max_area(int n) {
45 ll res = 0;
46 for (int i = 0; i < n; i++) {
47 int j = (i + 1) % n;
48 int k = (j + 1) % n;
49 while (i != j && j != k) {
50 while (k != i && cross(ch[j] - ch[i], ch[k + 1] - ch[i]) > cross(ch[j] - ch[i], ch[k] - ch[i]))
51 k = (k + 1) % n;
52 ll tmp = cross(ch[j] - ch[i], ch[k] - ch[i]);
53 if (res - tmp < 0) {
54 res = tmp;
55 resi = i;
56 resj = j;
57 resk = k;
58 }
59 j = (j + 1) % n;
60 }
61 }
62 }
63
64 int main() {
65 // freopen("case.in", "r", stdin);
66 int n;
67 ll s;
68 cin >> n >> s;
69 for (int i = 0; i < n; i++) {
70 scanf("%I64d%I64d", &p[i].x, &p[i].y);
71 }
72 int m = convex_hull(n);
73 max_area(m);
74 cout << ch[resj].x + ch[resk].x - ch[resi].x << ' ' << ch[resj].y + ch[resk].y - ch[resi].y << endl;
75 cout << ch[resi].x + ch[resk].x - ch[resj].x << ' ' << ch[resi].y + ch[resk].y - ch[resj].y << endl;
76 cout << ch[resi].x + ch[resj].x - ch[resk].x << ' ' << ch[resi].y + ch[resj].y - ch[resk].y << endl;
77 }