漫步最优化十四——凸函数与凹函数

我一直都在流浪，
可我却不曾见过海洋。
 我努力微笑坚强，
用寂寞筑成一道围墙。
如果恨你，就没发忘记你，
如果不够悲伤，就无法飞翔。
那就让我孤独到底，直到忘记了呼吸。
——畅宝宝的傻逼哥哥

通常在实际中，最小化的函数有几个极值，所以最优化算法得出的极值不确实是否为全局的极值，对于一些特殊的函数，凸函数与凹函数，任何局部极值也是全局极致，因此如果目标函数是凸的或凹的，那么优化算法就能保证是全局的。

定义1： 集合 Rc⊂En 是凸集，如果对每对点 x1,x2⊂Rc ，每个实数 α,0<α<1 ，点

x=αx1+(1−α)x2

位于 Rc ，即 x∈Rc 。

效果上，如果任何两点 x1,x2∈Rc 用直线相连， x1,x2 之间线上的每个点都在 Rc 中，那么 Rc 是凸的。如果存在点不在 Rc 中，那么该集合是非凸的，凸集合如图1所示。

凸的概念也可以用到函数上。

定义2：

1. 我们称定义在凸集 Rc 上的函数 f(x) 为凸的，如果对每对 x1,x2∈Rc 与每个实数 α,0<α<1 ，不等式
   
   f[αx1+(1−α)x2]≤αf(x1)+(1−α)f(x2)

满足。如果 x1≠x2

f[αx1+(1−α)x2]<αf(x1)+(1−α)f(x2)

满足，那么 f(x) 是严格凸的。

1. 如果 φ(x) 定义在凸集 Rc 上且 f(x)=−φ(x) 是凸的，那么 φ(x) 是凹的。如果 f(x) 是严格凸的，那么 φ(x) 是严格凹的。

上述定义中的不等式，左边是点 x1,x2 之间某处的 f(x) 值，而右边是基于线性插值得到的 f(x) 的近似，因此如果任何两点的线性插值大于函数的值，那么该函数就是凸的，图2a，b中的函数为凸的，2c为非凸的。

图1

定理1： 如果

f(x)=af1(x)+bf2(x)

其中 a,b≥0,f1(x),f2(x) 是凸集 Rc 上的凸函数，那么 f(x) 是集合 Rc 上的凸函数。

证明： 因为 f1(x),f2(x) 是凸函数， a,b≥0 ，所以对于 x=αx1+(1−α)x2 ，我们有

af1(αx1+(1−α)x2)≤a[αf1((x)1)+(1−α)f1(x2)]bf2(αx1+(1−α)x2)≤b[αf2((x)1)+(1−α)f2(x2)]

其中 0<α<1 ，因此

f(x)f(αx1+(1−α)x2)=af1(x)+bf2(x)=af1(αx1+(1−α)x2)+bf2(αx1+(1−α)x2)≤α[af1(x1)+bf2(x1)]+(1−α)[af1(x2)+bf2(x2)]

因为

af1(x1)+bf2(x1)=f(x1)af1(x2)+bf2(x2)=f(x2)

所以上面的不等式可以写成

f(αx1+(1−α)x2)≤αf(x1)+(1−α)f(x2)

即 f(x) 是凸函数。

图2

定理2： 如果 f(x) 是凸集 Rc 上的凸函数，那么对每个实数 K 而言，集合

Sc={x:x∈Rc,f(x)≤K}

都是凸集。

证明： 如果 x1,x2∈Sc ，那么根据 Sc 的定义， f(x1)≤K,f(x2)≤K ，因为 f(x) 是凸集，所以

f[αx1+(1−α)x2]≤αf(x1)+(1−α)f(x2)≤αK+(1−α)K

或者

f(x)≤Kfor x=αx1+(1−α)x2and0<α<1

所以

x∈Sc

即 Sc 是凸的。

定理2的图示如图3，其中集合 Sc 是凸集，如果 f(x) 在凸集 Rc 上是凸函数的话。

图3

另一种考虑凸的角度是测试 f(x) 的梯度与海森矩阵。

定理3： 如果 f(x)∈C1 ，那么 f(x) 在凸集 Rc 上是凸函数，当且仅当对所有 x,x1∈Rc

f(x1)≥f(x)+g(x)T(x1−x)

其中 g(x) 是 f(x) 的梯度。

证明： 这个定理的证明由两部分组成。首先我们证明如果 f(x) 是凸函数，那么不等式成立。然后证明如果不等式成立，那么 f(x) 是凸函数。首先如果 f(x) 是凸函数，那么对于所有 α,0<α<1

f[αx1+(1−α)x]≤αf(x1)+(1−α)f(x)

或者

f[x+α(x1−x)]−f(x)≤α[f(x1)−f(x)]

当 α→0 ，由 f[x+α(x1−x)] 的泰勒级数可得

f(x)+g(x)Tα(x1−x)−f(x)≤α[f(x1)−f(x)]

所以

f(x1)≥f(x)+g(x)T(x1−x)

接下来，如果不等式在 x,x2∈Rc 处成立，那么

f(x2)≥f(x)+g(x)T(x2−x)

从上面两式可得

αf(x1)+(1−α)f(x2)≥αf(x)+αg(x)T(x1−x)+(1−α)f(x)+(1−α)g(x)T(x2−x)

或者

αf(x1)+(1−α)f(x2)≥f(x)+gT(x)[αx1+(1−α)x2−x]

代入

x=αx1+(1−α)x2

可得

f[αx1+(1−α)x2]≤αf(x1)+(1−α)f(x2)

其中 0<α<1 ，因此 f(x) 是凸函数。

定理3说明 f(x) 在点 x 处基于 f(x) 导数的线性插值小于函数值，如图4所示。

定理4： 函数 f(x)∈C2 是凸集 Rc 上的凸函数，当且仅当 f(x) 的海森矩阵 H(x) 对 x∈Rc 是半正定的。

证明： 如果 x1=x+d ，其中 x1,x 是 Rc 中的任意点，那么由泰勒级数可得

f(x1)=f(x)+gT(x)(x1−x)+12dTH(x+αd)d

其中 0≤α≤1 ，接下来如果 H(x) 在 Rc 中是半正定的，那么

12dTH(x+αd)d≥0

所以

f(x1)≥f(x)+gT(x)(x1−x)

所以由定理3可知 f(x) 是凸函数。

如果 H(x) 在 Rc 任何处都是半正定的，那么存在点 x 与方向 d 使得

dTH(x+αd)<0

所以

f(x1)<f(x)+gT(x)(x1−x)

根据定理3可知 f(x) 是非凸的，所以当且仅当 H(x) 在 Rc 任何地方是半正定时 f(x) 是凸函数。

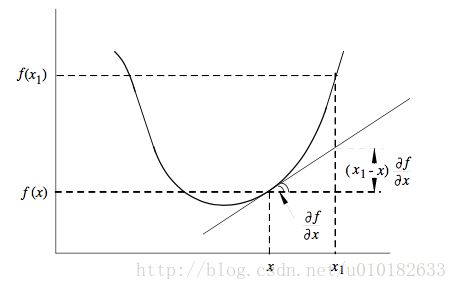
图4

对于严格凸函数，上面的定理修改如下：

定理5：

• 如果 f(x) 是凸集 Rc 上的严格凸函数，那么对每个实数 K 而言，集合
  
  Sc={x:x∈Rc,f(x)<K}

都是凸集。

• 如果 f(x)∈C1 ，那么 f(x) 在凸集 Rc 上的严格凸函数，当且仅当对所有 x,x1∈Rc
  
  f(x1)>f(x)+g(x)T(x1−x)

其中 g(x) 是 f(x) 的梯度。

• 函数 f(x)∈C2 是凸集 Rc 上的凸函数，当且仅当 f(x) 的海森矩阵 H(x) 对 x∈Rc 是正定的。

如果 φ(x) 定义在凸集 Rc 上，且 f(x)=−φ(x) 是严格凸函数，那么 φ(x) 是严格凹函数且其海森矩阵是负定的。反过来，如果 φ(x) 的海森矩阵是负定的，那么 φ(x) 是严格凹的。