2019牛客多校赛 第三场 D Big Interger（数论 + 组合计数）

 

 

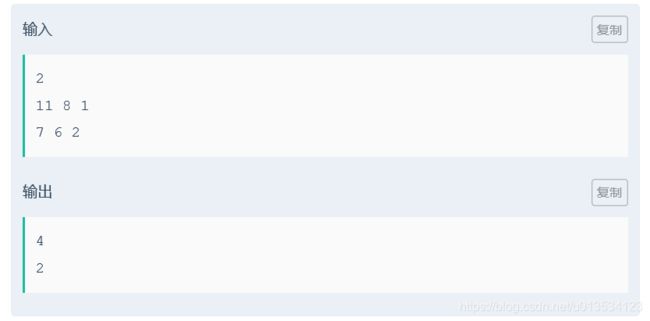
大致题意：一个数列为1,11,111,1111,......令A(n)表示这个序列的第n小的数字。告诉你p,n和m，让你求有多少对(i,j)可以使得，其中1<=i<=n，1<=j<=m，p为质数。

根据这个数列的形式，数列的第n项等于。那么我们相当于找到所有的，使得。

我们整理一下这个式子，可以得到：。

当时，，根据欧拉定理有。

但是这里不一定是最小的循环节，但是最小循环节一定是的因子。所以我们只需要枚举的每一个因子然后验证即可，这里复杂度为。这里我们假设最小循环节是x。

当我们找到x之后，问题就变成了找到所有的，使得。

对于这个问题，我们可以再次把式子拆开，把x和分解质因子，那么相当于要满足：

                           

其中,。可以看到关键部分在于i必须要含有所有的质因子，然后在确定i之后，j必须满足：。

显然，如果i取x的所有倍数，那么j可以取1..m的任何数字，因此这一部分的答案就是 。

接下来考虑不是x的倍数的情况，那么i至少含有质因子。根据j的限制条件，j的取值取决于，因此我们可以枚举这个起关键作用的质因子i和它的指数ai，让后限定其他的质因子的指数为满足条件的最小值，可以得到一个数字tmp。这样，n范围内所有能整除tmp且不能整除tmp*i的数字他们的j都是相同的，可以一起计算贡献。如此做即可，复杂度为x的因子个数乘上质因子个数，因此是级别的，总的复杂度也是的。具体见代码：

#include 
#define LL long long
#define pb push_back
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define file(x) freopen(#x".in","w",stdout);
#define bug(x) cerr<<#x<<": "< pri,t;

LL qpow(LL x,LL n,LL mod)
{
    LL res=1;
    while(n)
    {
        if (n&1) res=res*x%mod;
        x=x*x%mod; n>>=1;
    }
    return res;
}

LL qpow(LL x,LL n)
{
    LL res=1;
    while(n)
    {
        if (n&1) res=res*x;
        x=x*x; n>>=1;
    }
    return res;
}

inline bool check(int x)
{
    return qpow(10,x,p)==1;
}

int main()
{
    int T_T; sc(T_T);
    while(T_T--)
    {
        sccc(p,n,m);
        if (p==2||p==5)
        {
            puts("0");
            continue;
        }
        ans=0;
        if (p==3) x=3;
        else
        {
            int tmp=p-1; x=p-1;
            for(int i=2;i*i<=tmp;i++)
            {
                if (tmp%i) continue;
                if (check(i)) {x=i;break;}
                if (check(tmp/i)) x=min(x,tmp/i);
            }
            if (!check(x))
            {
                puts("0");
                continue;
            }
        }
        LL tmp=x;
        pri.clear(); t.clear();
        for(LL i=2;i*i<=tmp;i++)
        {
            if (tmp%i) continue;
            pri.pb(i); LL tt=0;
            while(tmp%i==0) tmp/=i,tt++;
            t.pb(tt);
        }
        if (tmp>1) pri.pb(tmp),t.pb(1);
        for(int i=0;i0);
                if (tt>m) continue; tmp=now;
                for(int k=i+1;k0));
                for(int k=i-1;k>=0;k--)
                    tmp*=qpow(pri[k],t[k]/(tt-1)+(t[k]%(tt-1)>0));
                if (tmp%x) ans+=(LL)(n/tmp-n/tmp/pri[i])*(m-tt+1);
            }
        }
        ans+=(LL)n/x*m;
        printf("%lld\n",ans);
    }

    return 0;
}
/*
233
9829 8800 5637
3331 2388 9584
97 235 654
*/