最短路径算法----Floyd-warshall（十字交叉算法证明）

Floyd不同于Dijkstra，可以得到所有点对的最短路径。使用的是DP

Floyd可以处理有负权重边的情况

递推公式：w(i, j) = min{w(i, j), w(i, k) + w(k, j)}，含义是【i到j的最短距离】=【i到k的最短距离+k到j的最短距离】与【i到j的最短距离】中较小的那一个

看起来很简单，但是具体怎么计算呢？

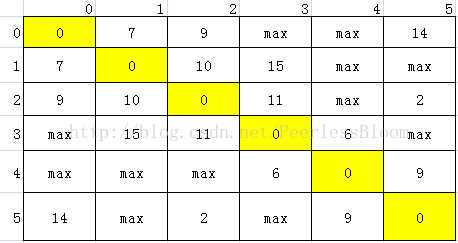
依旧使用这个例子，图的表示方式为：

[[0, 7, 9,  max,  max, 14],
 [7, 0, 10, 15, max, max],
 [9, 10, 0, 11, max, 2],
 [max, 15, 11, 0, 6, max],
 [max, max,  max,  6, 0, 9],
 [14,max,  2,  max, 9, 0]]

可以看出，w(i, i) = 0。这就是突破口了。

当k=0时，w(0, j)=min{w(0,0)+w(0,j), w(0,j)}；w(i,0)=min{w(i,0)+w(0,0), w(i,0)}，是不用更新的。当然，k不为0的时候，需要更新w(0,j)和w(i,0)

类似的，可以得到w(k,j)和w(i,k)不用更新。也就是说，和k相同行、列不用更新。

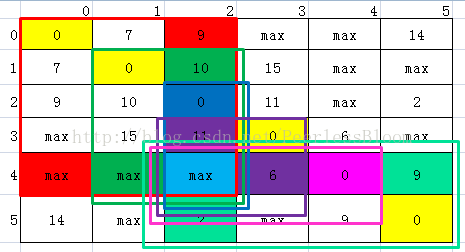
用图做个例子：求图中蓝色的值w(4,2)

w(4,2) = min{w(4,2) + 红色两个格子的和+绿色两个格子的和+紫色两个格子的和+薄荷色两个格子的和}

1. 可以看出k=2和k=4的时候，更新时没有意义的。

2. 可以看出，计算过程其实就是画一个(k,k)-(4,2)的方框，比较w(4,2)和方框的另外两个顶点w(4,k)+w(k,2)的大小。当然，这个时候w(4,k)和w(k,2)应该也是最优的解。

所以明显不能以i,j,k的loop顺序遍历。

那么试一下以k,i,j的loop顺序遍历呢？

这里有个很取巧的点：

1. 当k=0的时候，第一行、第一列已经是k=0的最优解了（还记得前面的结论吗）

2. 当k=0的时候，其他的行、列只用取第一行、第一列的数据

也就是说，当k=0的时候，遍历完整张图，能得到k=0的情况下dp算法的最优解：当且仅当中间节点编号<=0的时候，点i到点j的最近值

继续证明k=x的情况下最优解已经得到，k=x+1时继续遍历，能否得到k=x+1的最优解？

1. k=x+1的时候，第x+1行、第x+1列已经是k<=x+1的最优解了（k=x+1时，不用更新第x行、第x列）

2. k=x+1的时候，其他的行、列只会读取第x+1行、第x+1列的数据

因此当k=x+1时，遍历完整张图，能得到k=x+1的情况下dp算法的最优解。

证明完毕

以上的证明过程也就是“十字交叉算法”的原理了。

感兴趣的同学可以网上搜一下，瞬间即懂

def floyd(graph):
    # graph:n*n matrix
    # find min distance from start_node to end_node
    length = len(graph)
    for k in xrange(0, length):
        for i in xrange(0, length):
            for j in xrange(0, length):
                graph[i][j] = min(graph[i][k] + graph[k][j], graph[i][j])
    return graph

时间复杂度O(n^3)

驱动

graph = [[0, 7, 9,  max_int,  max_int, 14],
         [7, 0, 10, 15, max_int, max_int],
         [9, 10, 0, 11, max_int, 2],
         [max_int, 15, 11, 0, 6, max_int],
         [max_int, max_int,  max_int,  6, 0, 9],
         [14, max_int,  2,  max_int, 9, 0]]
print floyd(graph)

附录：

打印出最短路径

def floyd(graph):
    # graph:n*n matrix
    # find min distance from start_node to end_node
    length = len(graph)
    pre_node = [[-1 for i in xrange(0, length)] for j in xrange(0, length)]
    for k in xrange(0, length):
        for i in xrange(0, length):
            for j in xrange(0, length):
                dist = graph[i][k] + graph[k][j]
                if dist < graph[i][j]:
                    graph[i][j] = dist
                    pre_node[i][j] = k
    print "pre_node", pre_node
    return graph