牛客网暑期ACM多校训练营（第四场） A.Ternary String(欧拉降幂)

链接：https://www.nowcoder.com/acm/contest/142/A
来源：牛客网

题目描述
A ternary string is a sequence of digits, where each digit is either 0, 1, or 2.
Chiaki has a ternary string s which can self-reproduce. Every second, a digit 0 is inserted after every 1 in the string, and then a digit 1 is inserted after every 2 in the string, and finally the first character will disappear.
For example, 212'' will become11021” after one second, and become “01002110” after another second.
Chiaki would like to know the number of seconds needed until the string become an empty string. As the answer could be very large, she only needs the answer modulo (109 + 7).
输入描述:
There are multiple test cases. The first line of input is an integer T indicates the number of test cases. For each test case:
The first line contains a ternary string s (1 ≤ |s| ≤ 105).
It is guaranteed that the sum of all |s| does not exceed 2 x 106.
输出描述:
For each test case, output an integer denoting the answer. If the string never becomes empty, output -1 instead.
示例1
输入

复制
3
000
012
22
输出

复制
3
93
45

题意

给你一个只由 0,1,2 0 , 1 , 2 组成的串,每一秒都会消去串的第一个值，同样的每一秒串也会递增，串的递增条件是，如果是 1 1 ，每一秒 1 1 后面增加一个 0 0 ,如果是 2 2 ，每一秒增加一个 1 1 ，例如串为 2110 2110 ，第一秒过后串会变成 110100 110100 第二秒会变成 01001000 01001000 ，求串为空时的时间是多少秒对1e9+7取模

思路

我们考虑单个数在过了k秒后对时间的贡献，设已经过了k秒
首先考虑 0 0 ，因为 0 0 不会增生所以不管已经过了多少秒他对时间的贡献都是 1 1
然后考虑 1 1 ，例如已经过了2秒了，下一秒要消去的是1，那么到了下一秒剩下的串就会变成 000 000 ，那么时间就变成了 3 3 ，再加上3个 0 0 所以时间就变成了6

012⋮k246⋮2k+2 0 2 1 4 2 6 ⋮ ⋮ k 2 k + 2

找一下规律会发现，如果已经过了 k k 秒，那么消去这个 1 1 和他的贡献的时间就会变成 2k+2 2 k + 2
然后我们再考虑 2 2 的贡献每过一秒实际上就会多有一个1，每个1的是 2k 2 k 的那么自然是与 2k 2 k 有关，所以我们考虑和2的次幂有关然后就可以找到这个规律了

013⋮k3819⋮3∗2k+1−3 0 3 1 8 3 19 ⋮ ⋮ k 3 ∗ 2 k + 1 − 3

现在有了3个公式就可以来解决问题了，但是如果对时间取模，当其遇到2的次幂的时候就会错误
我们我们可以把过程看作一个在2的次幂上操作的过程例如
这个序列

0011211212 0011211212

一开始 t=0 t = 0 ，然后我们看看这是一个怎么样的过程

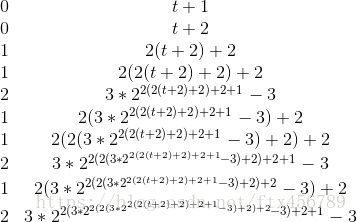
我们可以把他看作是 222222222222⋅⋅⋅%mod 2 2 2 2 2 2 2 2 2 2 2 2 ⋅ ⋅ ⋅ % m o d
那么我们可以用欧拉降幂的方式来递归处理这样的式子

ax≡ax%ϕ(p)+ϕ(p)(modp) a x ≡ a x % ϕ ( p ) + ϕ ( p ) ( m o d p )

若 x x 也为一个次幂的式子那么我们可以继续带入这个式子，也就是说

实际上我们只要知道2有多少个就可以解决这个问题了，我们递归一下 mod=1000000007 m o d = 1000000007 的 ϕ ϕ
一共到28个就到1了，也就是从最后一个2开始数2的个数，只用计算后28个的2就可以了
记录一下每个区间要用哪一个 ϕ ϕ 来模就好了

#include
#include
#include
#include
using namespace std;
int a[100010];
char s[100010];
const long long mod = 1e9 + 7;
long long quickmod(long long a, long long b,long long mod)
{
    long long ans = 1;
    a = a % mod;
    while (b)
    {
        if (b % 2 == 1)
            ans = ans * a%mod;
        b = b / 2;
        a = a * a%mod;
    }
    return ans%mod;
}
long long phi(long long n)
{
    long long res=n;
    for(long long i=2; i*i<=n; i++)
    {
        if(n%i==0)
        {
            res=res-res/i;
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1)
        res=res-res/n;
    return res;
}
long long p[30];
int main()
{
    p[0]=p[1]=mod;
    int cnt=0;
    for(int i=2;;i++)
    {
        p[i]=phi(p[i-1]);
        if(p[i]==1)
        {
            cnt=i;
            break;
        }
    }
    int t, n;
    cin >> t;
    while (t--)
    {
        int n = 0;
        scanf("%s", s);
        n = strlen(s);
        for (int i = 0; i < n; i++)
        {
            a[i] = s[i] - '0';
        }
        int num=0;
        int pos=0;
        for(int i=n-1;i>=0;i--)
            {
                if(a[i]==2)
                num++;
                if(num==28)
                {
                    pos=i;
                    break;
                }
            }
        long long ans = 0;
        num++;
        for (int i = pos; i < n; i++)
        {
            if (a[i] == 0)
                {
                    ans = (ans + 1) % p[num];
                }
            if (a[i] == 1)
                {
                    ans = (2*ans%p[num] + 2%p[num]) % p[num];
                }
            if (a[i] == 2)
            {
                num--;
                ans = ((long long)3%p[num] * quickmod(2, ans + 1,p[num])) % p[num];
                ans = (ans%p[num] - 3 + p[num]) % p[num];
            }
        }
        printf("%lld\n", ans%mod);
    }
}