1 算法分析
1.1 摊还分析
摊还分析是用来评价程序中的一个操作序列的平均代价,有时可能某个操作的代价特别高,但总体上来看也并非那么糟糕,可以形象的理解为把高代价的操作“分摊”到其他操作上去了,要求的就是均匀分摊后的平均代价。
摊还代价:对所有n,一个n个操作的序列最坏情况下话费时间为T(n),从而摊还代价(平均代价)为 T(n) / n.
1.2 大O
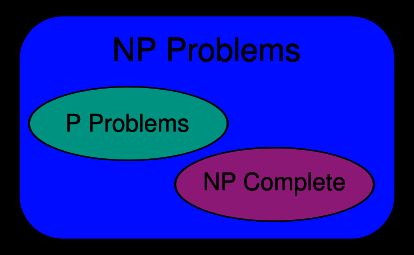
O(1) NP:Non-deterministic Polynomial 首先需要介绍P(Polynomial,多项式)问题.P问题是可以在多项式时间内被确定机(通常意义的计算机)解决的问题.NP(Non-Deterministic Polynomial, 非确定多项式)问题,是指可以在多项式时间内被非确定机(他可以猜,他总是能猜到最能满足你需要的那种选择,如果你让他解决n皇后问题,他只要猜n次就能完成----每次都是那么幸运)解决的问题.这里有一个著名的问题----千禧难题之首,是说P问题是否等于NP问题,也即是否所有在非确定机上多项式可解的问题都能在确定机上用多项式时间求解. 首先需要介绍P(Polynomial,多项式)问题.P问题是可以在多项式时间内被确定机(通常意义的计算机)解决的问题.NP(Non-Deterministic Polynomial, 非确定多项式)问题,是指可以在多项式时间内被非确定机(他可以猜,他总是能猜到最能满足你需要的那种选择,如果你让他解决n皇后问题,他只要猜n次就能完成----每次都是那么幸运)解决的问题.这里有一个著名的问题----千禧难题之首,是说P问题是否等于NP问题,也即是否所有在非确定机上多项式可解的问题都能在确定机上用多项式时间求解. 死锁是两个或者多个相互竞争的进程都在等待对方使用完并释放资源,然而却形成了一个资源请求环,使得都不能如愿。 活锁与死锁类似,只是进程的状态仍会改变(从缺铅笔到缺直尺)。 监视器和锁在Java虚拟机中是一块使用的。监视器监视一块同步代码块,确保一次只有一个线程执行同步代码块。每一个监视器都和一个对象引用相关联。线程在获取锁之前不允许执行同步代码。 相同点:Mutex和Monitor都只能有一个线程拥有锁定。 Semaphore,是负责协调各个线程, 以保证它们能够正确、合理的使用公共资源。也是操作系统中用于控制进程同步互斥的量。 图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为G(V,E),其中,G标示一个图,V是图G中顶点的集合,E是图G中边的集合。 Hash表或hash map使用Hash函数来映射特定的键(Key)到对应的值(value)。 有些链接法的实现在数组槽中存放对应hash值的第一个记录。 堆是一种基于树的数据结构,分为最大堆和最小堆。堆可以有数组实现,a[2n]、a[2n+1]是a[n]的子节点。 Fibonacci堆能实现更高的时间效率。 线性表有两种存储方式,一种是顺序存储结构,另一种是链式存储结构。链表就是链式存储的线性表。根据指针域的不同,链表分为单向链表、双向链表、循环链表等等。 高优先权优先(highest-priority-first) 使用可盖写的循环队列的一个例子是多媒体。 start指针指向有效数据的开始。 栈是一个后进先出的数据结构。 B树是二叉树的泛化版,允许节点有超过两个子节点。 AVL在计算机科学中是最先发明的自平衡二叉查找树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis。 类似二元搜索树。 红黑树是一种自平衡二元搜索树。 将待访问的数据放入一个queue中保存。 先构造堆,然后依次删除数据,得到排序的结果。构造堆的过程并不是依次加入节点来构造,效率也相对较高。 分而治之的算法。选择一个pivot将数据分为大小两半,然后在这两部分递归使用快排。 分到甚至每个组只有零个或一个元素,然后对相邻组进行合并,直到最后一次合并所有元素。1.3 NP复杂性
NP问题即多项式复杂程度的非确定性问题。
首先需要介绍P(Polynomial,多项式)问题.P问题是可以在多项式时间内被确定机(通常意义的计算机)解决的问题.NP(Non-Deterministic Polynomial, 非确定多项式)问题,是指可以在多项式时间内被非确定机(他可以猜,他总是能猜到最能满足你需要的那种选择,如果你让他解决n皇后问题,他只要猜n次就能完成----每次都是那么幸运)解决的问题.这里有一个著名的问题----千禧难题之首,是说P问题是否等于NP问题,也即是否所有在非确定机上多项式可解的问题都能在确定机上用多项式时间求解.1.3.1 NP完全
NP-complete问题通常使用近似算法求解。1.3.2 P复杂性
1.4 图灵机
1.5 锁
1.5.1 死锁
现实生活中就比如两个人画画,总共只有一只铅笔一个直尺,两人各自拿一样工具并请求对方的工具。1.5.2 活锁
现实生活中的例子就比如两人狭路相逢,每个人都礼貌地避让到另一边,结果两人一直左右摇摆,谁都过不去。1.5.3 监视器(monitor)
1.5.4 互斥量(mutex=Mutual exclusion)
不同点:Mutex可用于进程内的线程同步,也可用于进程同步,一般用于进程同步。Monitor则只能用于进程内的线程同步。当进行进程内的线程同步时,优先选择Monitor。因为Monitor应用在用户模式下的线程同步技术,而Mutex是应用于内核级别的线程同步技术,线程的执行是在用户模式下执行的,而要切换到内核模式大概要消耗1000个CPU时钟,所以进行进程内的线程同步时优先选择Monitor,而进行进程间的同步时,Mutex是不二之选。1.5.5 信号量(semaphore)
以一个停车场是运作为例。为了简单起见,假设停车场只有三个车位,一开始三个车位都是空的。这时如果同时来了五辆车,看门人允许其中三辆不受阻碍的进入,然后放下车拦,剩下的车则必须在入口等待,此后来的车也都不得不在入口处等待。这时,有一辆车离开停车场,看门人得知后,打开车拦,放入一辆,如果又离开两辆,则又可以放入两辆,如此往复。2 数据结构
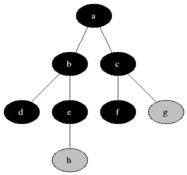
2.1 图
2.1.1 图的表示(representations)
邻接链表最受青睐,因为它是可以高效地表示稀疏图。对于稠密的图,则倾向于使用邻接矩阵。2.2 Hash表
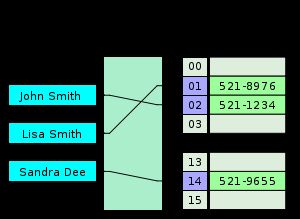
2.2.1 分离链接(seperate chaining)
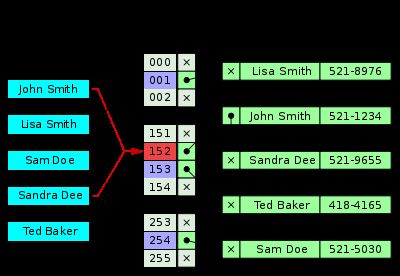
2.2.1 带表头的分离链接法(seperate chainning with list head)
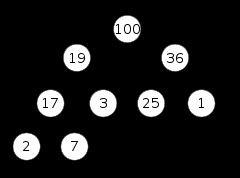
2.3 堆
2.3.1 应用
2.3.2 时间计算
2.4 链表
2.5 队列
2.5.1 双端队列(double-ended queue abbr. deque)
2.5.2 优先队列
2.5.3 循环缓冲(循环队列)
2.5.3.1 start/end指针
end指针指向有效数据的结尾。2.6 栈
2.7 树
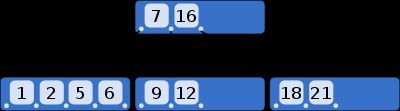
2.7.1 B树(balanced tree)
B-树的存在是为了优化系统读写大块的数据(使用多叉减少访问内存的次数)。常用于数据库和文件系统。2.7.1.1 搜索
2.7.1.2 删除(deletion)
2.7.1.2.1 从叶子节点检测
2.7.1.2.2 从内部节点检测
2.7.1.2.3 检查后的重平衡(rebalance)
2.7.2 红黑树
2.7.3 Trie或前缀树
算法
3.1 搜索
3.1.1 二元搜索
public class BinarySearch{
static int search(int[] A, int k){
int b = 0;
int e = A.length - 1;
int m;
while( b <= e ){
m = 1 + (e-1)/2;
if(A[m] < K){
b = m+1;
}else if( A[m] == k ){
return m;
}else{
e = m - 1;
}
}
return -1;
}
3.1.2 宽度优先搜索(on graphs)
3.1.3 深度优先搜索(on graphs)
3.2 排序
3.2.1 堆排序
3.2.1.1 例子
3.2.2 快速排序
3.2.3 合并排序