单调栈及其应用——以LeetCode(42) 接雨水，LeetCode（84）柱状图最大的矩形为例

大家都知道，栈是一种常用的数据结构，有一定的数据操作和使用的规则，单调栈是使用栈来实现的一种算法，之所以将单调栈称为一种算法就是因为它是用来解决某一类问题的，还没有通用到可以解决很多的问题，或者作为其他算法的基本元素。单调栈只是栈的一种用法。
下面介绍单调栈的定义及性质

单调栈

1.单调栈分为单调递增栈和单调递减栈
11. 单调递增栈即栈内元素保持单调递增的栈
12. 同理单调递减栈即栈内元素保持单调递减的栈

2.操作规则（下面都以单调递增栈为例）
21. 如果新的元素比栈顶元素大，就入栈
22. 如果新的元素较小，那就一直把栈内元素弹出来，直到栈顶比新元素小

3.加入这样一个规则之后，会有什么效果
31. 栈内的元素是递增的
32. 当元素出栈时，说明这个新元素是出栈元素向后找第一个比其小的元素

4.什么问题适合用单调栈
41.找一个值后第一个小于该值的点的情况可以用单调递增栈
42.找一个值后第一个大于该值的点的情况可以用单调递增栈

利用单调栈遍历，时间复杂度为O(n)

代码模板（cpp）

stack<int> st;
for(int i = 0; i < nums.size(); i++)
{
	while(!st.empty() && st.top() > nums[i])
	{
		st.pop();
	}
	st.push(nums[i]);
}

接雨水

问题描述：

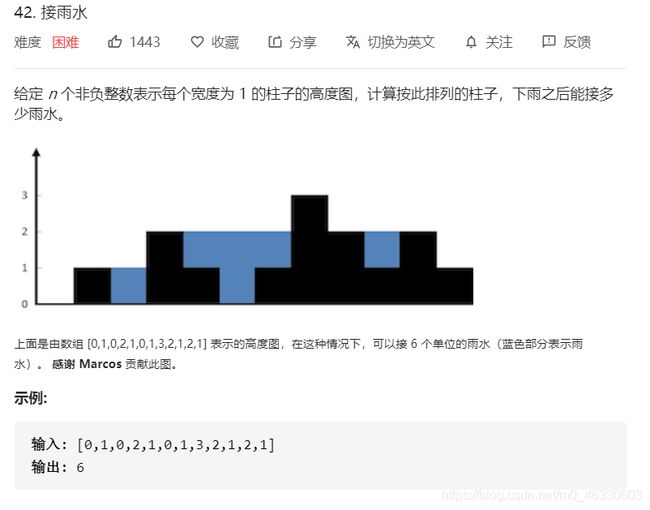
问题分析：
注意到只有中间的数值比两边小时才可以接到雨水，所以需要找每个点两边第一个比该点值大的点。因此，我们可以利用单调递减栈来完成这题。
下面演示单调递减栈对于[4, 3, 1, 0, 1, 2, 4]是怎么接雨水的，下图是最终的接雨水效果，蓝色部分是雨水。
可以看下下面的图示。图示最上方是每个柱子的高度。左侧是单调栈的元素，0是栈顶。图中有红色边框的柱子是存在单调栈里的元素。
遍历到图示中箭头所指向的位置时，栈内元素是[4, 3, 1, 0]。由于当前的柱体的1大于栈顶元素0，那就可以接住雨水。接住雨水的量的高度是栈顶元素和左右两边形成的高度差的min。宽度是1。

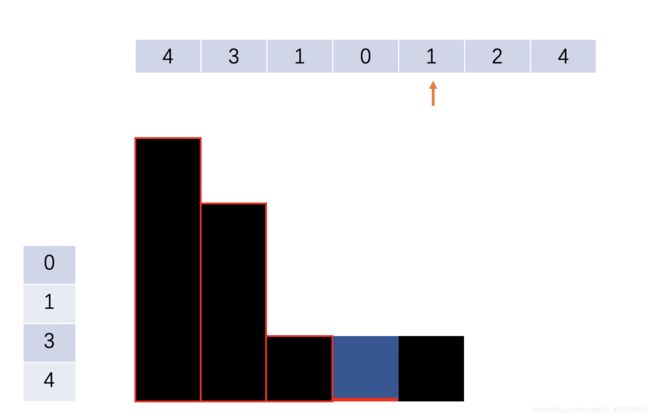
到下一个柱体高度为2时，栈内元素是[4, 3, 1, 1]。由于当前的柱体的2大于栈顶元素1，那就可以接住雨水。由于栈顶元素有相等的情况，所以可以把1全都pop出去，变成[4, 3]。此时最后一个pop出去的是1，高度是此时的栈顶元素和当前2柱体的高度的min再减去当前的1，宽度是1那个数字的位置和当前2柱体所在位置的差值。 可以算出来此次接住的雨水是1 * 3。

在下一个柱体高度为4时，栈内元素是[4, 3, 2]，先把2pop出来，栈顶元素3所在位置和当前的4可以接住雨水，雨水量是 1 * 4。
但是由于栈顶元素3仍然小于当前的4,再pop出3。栈顶元素4所在位置和当前的4可以接住雨水，雨水量是 1 * 5：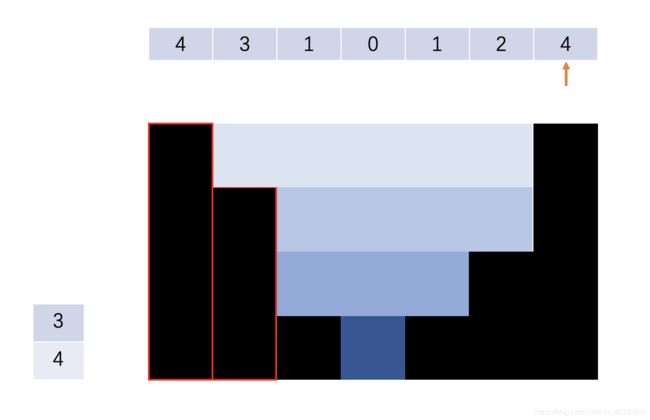
这样每个部分的雨水量都可以算出来，加在一起就可以了。由于每个柱体最多入栈出栈一次，所以时间复杂度是 O(n)。
源代码（c）

int trap(int* height, int heightSize){
    int top=-1,t[100],i,s=0,k,h;
    for(i=0;i<heightSize;i++){
        while(top>=0&&height[t[top]]<height[i]){
            if(top==0){
                top--;
                break;
            }
            k=height[t[top--]];
            if(height[i]<height[t[top]])h=height[i]-k;
            else h=height[t[top]]-k;
            s+=h*(i-t[top]-1);
        }
        t[++top]=i;
    }
    return s;
}

柱状图最大的矩形

问题描述：


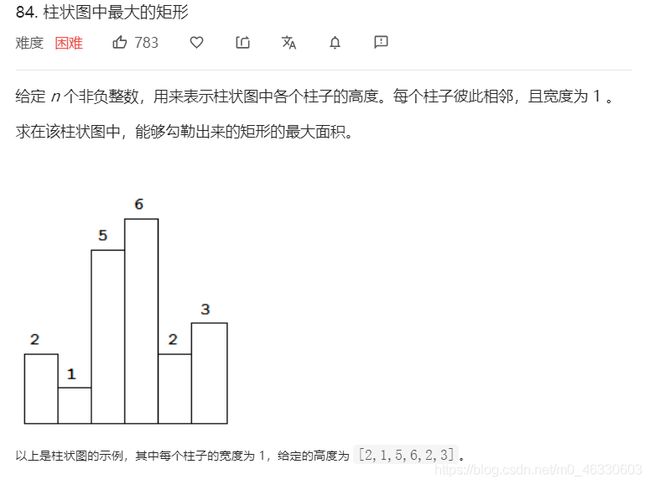
问题分析：
对于每个高度的矩形，我们需要知道其高度和宽度来求面积。高度可以直接知道，宽度要找到左边第一个小于该值的点和右边第一个小于该值的点。因此，我们可以用单调递增栈从左往右遍历来解决这个问题。
对于每个出栈的点，由于栈是单调递增的，其出栈后新的栈顶元素便是左边第一个比其小的点，而准备进来的新元素则是右边第一个比其小的点，因此宽度可以用这两个点的下标只差-1即可得到。
为了让所有元素都出栈，我们可以加入哨兵，在数组的左右各加一个0。
源代码（c）

int largestRectangleArea(int* heights, int heightsSize){
    if(!heightsSize){
        return 0;
    }
    if(heightsSize==1){
        return heights[0];
    }
    int t[heightsSize+2],top=-1,i,k,ans=0,cpy[heightsSize+2];
    cpy[0]=0;cpy[heightsSize+1]=0;
    for(i=0;i<heightsSize;i++){
        cpy[i+1]=heights[i];
    }
    for(i=0;i<heightsSize+2;i++){
        while(top>=0&&cpy[t[top]]>cpy[i]){
            k=t[top--];
            if(ans<(cpy[k]*(i-t[top]-1))){
                ans=cpy[k]*(i-t[top]-1);
            }
        }
        t[++top]=i;
    }
    return ans;
}