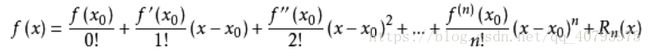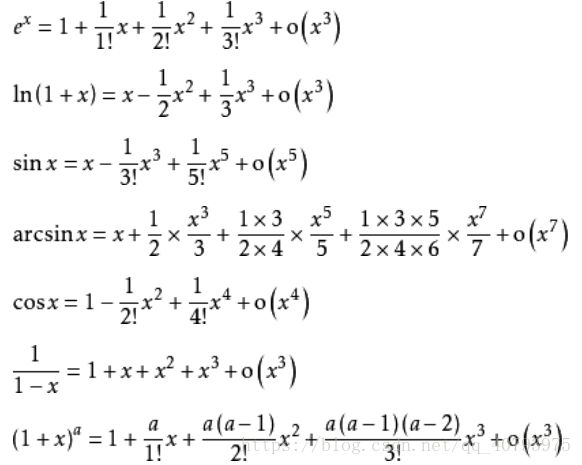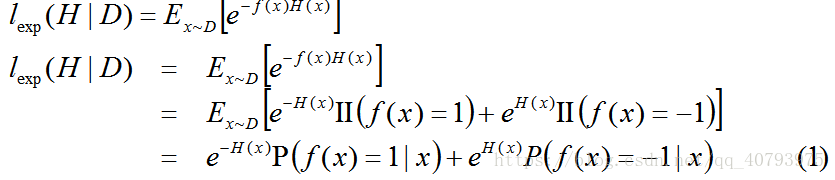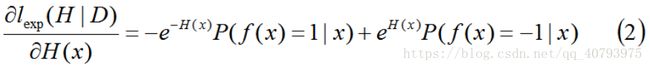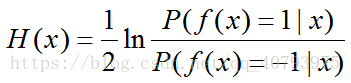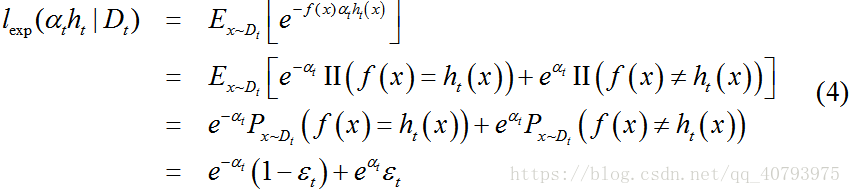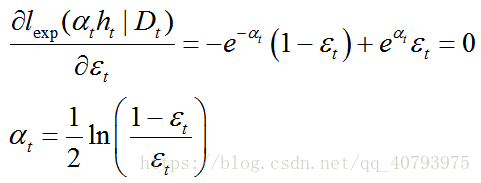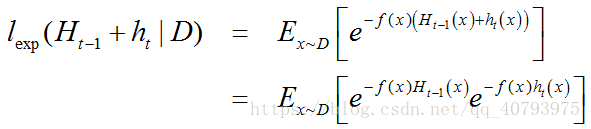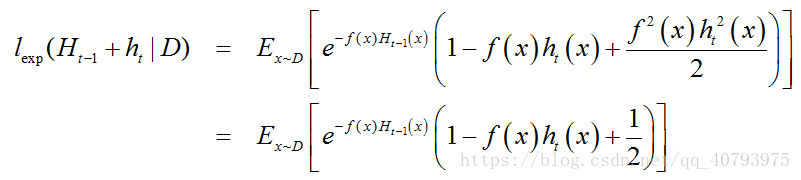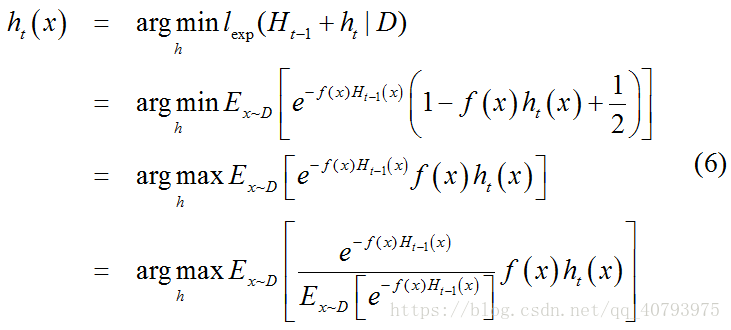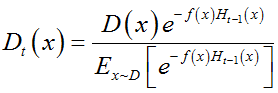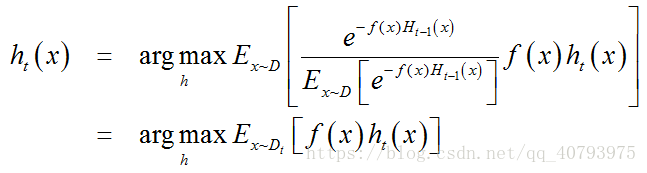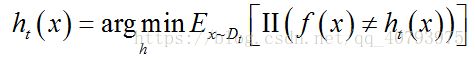Adaboost详解（附带基本公式推导）

Adaboost详解

第一次写博客，本人数学基础不是太好，如果有幸能得到读者指正，感激不尽，希望能借此机会向大家学习。这一篇的大部分内容都来自于《机器学习》这本书，以及自己的一些见解。MathJax还不会用，so公式都是我用MathType打出来后截图生成的。

预备知识：

这一部分主要是谈一谈Boosting的概念和原理，以及Adaboost中涉及到的基础数学公式以及定理的推导。

弱学习器

  弱学习器常指泛化性能略优于随机猜测的学习器，例如在二分类问题上精度略高于50%的分类器。——《机器学习》周志华 P171

Boosting（提升）

  Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似：先从初始训练集训练出一个基学习器，再根据基学习器的表现队训练集样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此反复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权结合。——《机器学习》周志华 P173

加性模型（additive model）

$$H\left(x\right)=\sum _{t=1}^T{\alpha }_t{h}_t\left(x\right)$$

其中，${\alpha }_t$为每个基学习器的权值，$h_t\left(x\right)$为每个基学习器的预测结果。

数学期望的一条重要定理

  若存在$x\in \mathrm{X},y\in \mathrm{Y}$，且存在这样的映射$\mathrm{Y}=f\left(\mathrm{X}\right)$，则可以得到，

$$E_{\left(y\right)}=f\left(E_{\left(x\right)}\right)$$

其中，$E_{\left(x\right)}$、$E_{\left(y\right)}$分别为$x$和$y$的期望。

泰勒展开式

其中，$f^{\left(n\right)}\left(x\right)$表示$f\left(x\right)$的n阶导数，等号后的多项式称为函数$f\left(x\right)$在$x_0$处的泰勒展开式，剩余的$R_n\left(x\right)$是泰勒公式的余项，是${\left(x-x_0\right)}^n$的高阶无穷小。
  以下列举一些常用函数的泰勒公式：

推导过程

主要分为三部分：指数损失函数、基学习器的权值$ \alpha_t $的更新和训练集样本分布$ D_t\left(x\right) $的更新。

指数损失函数

  若$f\left(x\right)$为样本$x$的实际标签值，$H\left(x\right)$为样本的预测标签值，则指数损失函数可以表示为，

其中$E_{x\stackrel{~}{}D}\left[e^{-f\left(x\right)H\left(x\right)}\right]$为样本服从分布$D$时，$e^{-f\left(x\right)H\left(x\right)}$的期望值，$\mathrm{I}\mathrm{I}\left(f\left(x\right)=1\right)$当$f\left(x\right)=1$时，等于1，否则为0。
  若存在$H\left(x\right)$使得$l_{exp}\left(H|D\right)$可以最小化，则可以将式子（1）对$H\left(x\right)$求偏导数，即

  令式子（2）为零，得到

  从而得到，

  这证明$\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(H\left(x\right)\right)$达到了最小贝叶斯最优错误率。换言之，若指数损失最小化，则分类错误率也将最小化，这说明指数损失函数是分类任务原本0/1损失函数的一致的替代函数，由于其具有良好的数学性质，因此用它替代0/1损失函数作为优化目标。

基学习器的权值${\alpha }_t$的更新

  当基学习器$h_t\left(x\right)$基于分布$D_t$产生后，该基学习器的权重${\alpha }_t$应使得${\alpha }_t{h}_t$最小化指数损失函数

上式中${\epsilon }_t=P_{x\stackrel{~}{}D}\left(f\left(x\right)̸=h_t\left(x\right)\right)$为加权误差，误差权值即为样本权值，为了最小化式子（4），将其对求偏导数并置零，得到

这样就得到了基学习器的权值更新公式。

训练集样本分布$D_t\left(x\right)$的更新

  在获得基学习器$h_{t-1}\left(x\right)$后，样本分布将进行调整，使下一轮基学习器$h_t\left(x\right)$能纠正$H_{t-1}$（集成了前$t-1$个学习器后的集成学习器）的全部错误，即最小化

注意到$f^2\left(x\right)=h_t^2\left(x\right)=1$，上式中$e^{-f\left(x\right)h_t\left(x\right)}$经过泰勒展开【5】后得到

  于是，理想的基学习器

式子（6）中$E_{x\stackrel{~}{}D}\left[e^{-f\left(x\right)H_{t-1}\left(x\right)}\right]$是一个常数，令$D_t$表示一个分布，即

根据数学期望的定理【4】，可以将式子（6）转化为

由$f\left(x\right),h_t\left(x\right)\in \{-1,1\}$，有如下关系式

则理想学习器为

由此可见，理想的基学习器$h_t\left(x\right)$将在分布$D_t\left(x\right)$下最小化分类误差，因此$h_t\left(x\right)$应该基于分布$D_t\left(x\right)$来训练。由$D_t\left(x\right)$和$D_{t-1}\left(x\right)$的关系，可以得到

上式即为样本分布的更新公式。

Adaboost伪代码

代码实现及对比

下面是我根据《机器学习实战》上的源代码自己实现的代码，对于不满足弱学习器的基学习器进行了处理，防止由于基学习器的性能过低而导致集成学习器的性能下降，另外当某个阶段的集成学习器可以达到对训练集完全正确的分类时，继续进行迭代会产生和前面完全一样的冗余的基学习器，因此这时要停止迭代的进行。

代码细节

"""

@author: Ἥλιος
@CSDN：https://blog.csdn.net/qq_40793975/article/details/80088381

"""


import numpy as np
import matplotlib.pyplot as plt


# 加载一个简单的数据集
def load_simpleData():
    data_mat = np.mat([[1., 2.1], [2., 1.1], [1.3, 1.], [1., 1.], [2., 1.]])
    label_mat = np.array([1.0, 1.0, -1.0, -1.0, 1.0])
    label_mat = np.mat(label_mat, dtype=np.int).T   # 为label_mat增加一维
    return data_mat, label_mat


# 根据指定的属性、阈值、阈值范围，来对数据进行分类
def stump_classify(data_mat, feat_index, thresh_val, thresh_ineq):
    ret_array = np.mat(np.ones((np.shape(data_mat)[0], 1)), dtype=np.int)
    if thresh_ineq == 'lt':
        ret_array[data_mat[:, feat_index] <= thresh_val] = -1.0
    else:
        ret_array[data_mat[:, feat_index] > thresh_val] = -1.0
    return ret_array


# 构建决策树桩作为基学习器（sample_weight是用来计算总误差的各样本权重）
def build_stump(data_mat, label_mat, sample_weight):
    m, n = np.shape(data_mat)
    min_error = np.inf  # 使用各种不同划分方式得到的最小误差
    best_stump = {}  # 构建出来的最佳决策树桩信息
    best_label = np.mat(np.zeros((m, 1)))
    step_num = 10
    for feat_index in range(n):
        feat_max = np.max(data_mat[:, feat_index])
        feat_min = np.min(data_mat[:, feat_index])
        step_value = (feat_max - feat_min) / step_num
        for step in range(-1, step_num + 1):
            thresh_val = feat_min + step*step_value
            for thresh_ineq in ['lt', 'gt']:
                error_array = np.mat(np.ones((m, 1)))   # 初始化误差向量
                label_array = stump_classify(data_mat, feat_index, thresh_val, thresh_ineq)
                error_array[label_array == label_mat] = 0  # 将划分正确的样本误差设置为零
                # currrnt_error = (sample_weight.T * error_array) / m   # 计算当前划分模式下的平均加权误差
                currrnt_error = sample_weight.T * error_array
                if currrnt_error < min_error:
                    best_stump["feat_index"] = feat_index  # 最小误差对应的特征索引
                    best_stump["thresh_val"] = thresh_val   # 最小误差对应的划分阈值
                    best_stump["thresh_ineq"] = thresh_ineq  # 最小误差对应的划分阈值范围
                    min_error = currrnt_error
                    best_label = label_array
    return best_stump, min_error, best_label


# 训练Adaboost集成学习器（num_iter是迭代次数，也是基学习器的数量）
def adaboost_trainer(data_mat, label_mat, num_iter=10):
    base_learnerArray = []
    m, n = np.shape(data_mat)
    sample_weight = np.mat(np.ones((m, 1)), dtype=np.float32) / m  # 初始化各样本权重
    prediction_array = np.zeros((m, 1), dtype=np.float32)
    while num_iter:
        base_bestStump, base_leanerError, base_learnerLabel = \
            build_stump(data_mat, label_mat, sample_weight)   # 这里使用带权重的数据集训练# 基学习器，来替代随机抽样
        while base_leanerError > 0.5:  # 如果得到的基学习器并不满足弱学习器的条件，那么就重新初始化样本权重，并重新训练一个新的基学习器
            sample_weight = np.mat(np.ones((m, 1)), dtype=np.float32) / m  # 初始化各样本权重
            base_bestStump, base_leanerError, base_learnerLabel = \
                build_stump(data_mat, label_mat, sample_weight)
        print("Base_leanerError:", float(base_leanerError))
        alpha = float(np.log((1 - base_leanerError) / base_leanerError) / 2)
        print("Alpha:", alpha)
        print("Base_learnerLabel:", base_learnerLabel.T)
        print("Real_label:", label_mat.T)
        base_bestStump["alpha"] = alpha
        base_learnerArray.append(base_bestStump)
        prediction_array += base_learnerLabel*alpha
        error_rate = np.sum(np.sign(prediction_array) != label_mat) / m
        num_iter -= 1
        expon = np.multiply(-1*alpha*label_mat, base_learnerLabel)
        sample_weight = np.multiply(sample_weight, np.exp(expon))
        sample_weight = sample_weight / np.sum(sample_weight)
        print("Sample_weight:", sample_weight.T)
        print("Current Error: ", error_rate)
        print("=========================")
        if error_rate == 0:
            break
    return base_learnerArray


data_mat, label_mat = load_simpleData()
print(adaboost_trainer(data_mat, label_mat))


# 使用Adaboost进行预测
def adaboost_predictor(data_matPredict, base_learnerArray):
    m = np.shape(data_matPredict)[0]
    label_matPredict = np.mat(np.zeros((m, 1)), dtype=np.float32)
    for base_learner in base_learnerArray:
        label_matBase = \
            stump_classify(data_matPredict, base_learner["feat_index"],
                           base_learner["thresh_val"], base_learner["thresh_ineq"])
        label_matPredict += base_learner["alpha"] * label_matBase
    return np.sign(label_matPredict)


# 从文件中加载数据集
def load_textData(filename):
    data_mat = []
    label_mat = []
    with open(filename) as fr:
        for line in fr.readlines():
            current_line = [float(i) for i in line.strip().split("\t")]
            data_mat.append(current_line[:-1])
            label_mat.append(current_line[-1])
    data_mat = np.mat(data_mat)
    label_mat = np.mat(label_mat).T
    return data_mat, label_mat


# data_matT, label_matT = load_textData("C:\\Users\\Administrator\\Desktop\\Adaboost\\horseColicTraining2.txt")
# base_learnerArray = adaboost_trainer(data_matT, label_matT, 50)
# data_matP, label_matP = load_textData("C:\\Users\\Administrator\\Desktop\\Adaboost\\horseColicTest2.txt")
# label_matPreduct = adaboost_predictor(data_matP, base_learnerArray)
# error_rate = np.sum(label_matP != label_matPreduct) / np.shape(data_matP)[0]
# print("Error rate: ", error_rate)

  这个代码只实现了简单的二分类，没有对其他情况进行处理，另外，原始算法伪代码中首先通过对原始数据集根据样本权重进行随机抽样得到一个相同大小数据集，然后用这个数据集作为基学习器的训练集，另一种引入样本权重的方法是直接在训练基学习器时使用原始数据集并考虑样本权重对基学习器学习目标的影响，该代码采用的是第二种方法引入样本权重的影响，在训练基学习器（决策树桩）时，采用加权误差代替一般分类误差。

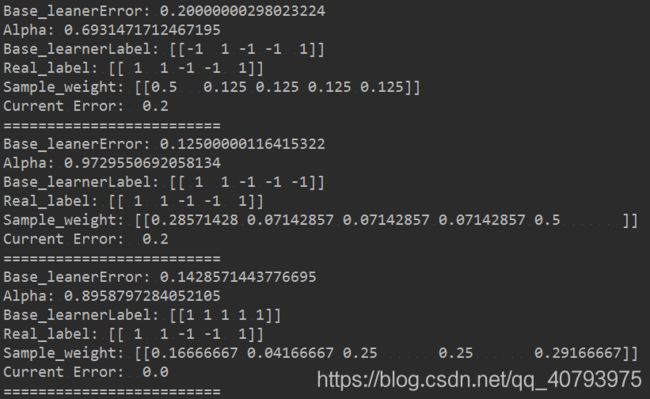
算法效果

  上图是在一个简单的事例数据集上运行的效果，可以看出集成学习器的整体误差Current Error在不断下降，当基学习器的误差Base_learnerError较大时，其在集成学习器中所占的权重Alpha较小，另外对于在该轮迭代中被分类错误的样本点，会增加他在整个数据集中所占的权重。

  上图是在一个较大的数据集上运行的实例，可以看出在训练过程中，整体分类误差Current Error在不断下降，由于区域有限不在此贴出整个训练过程，Error rate是在测试集上的分类误差。

数据集

horseColicTraining2.txt
horseColicTest2.txt

---

参考资料

【1】《机器学习》周志华
【2】泰勒公式——百度百科
【3】数学期望——百度百科
【4】《机器学习实战》