2016 Multi-University Training Contest 10题解报告
此文章可以使用目录功能哟↑(点击上方[+])
大学阶段的最后一场多校了,着实有些不舍,没有等到自己变得强大,就结束了征程。
一个人撸一下午的题,果然还是比较吃力的,居然是因为时间不够才出了4题,没办法,剩下的只能赛后补了...
链接→2016 Multi-University Training Contest 10
Problem 1001 Median
Accept: 0 Submit: 0
Time Limit: 6000/3000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
There is a sorted sequence A of length n. Give you m queries, each one contains four integers, l1, r1, l2, r2. You should use the elements A[l1], A[l1+1] ... A[r1-1], A[r1] and A[l2], A[l2+1] ... A[r2-1], A[r2] to form a new sequence, and you need to find the median of the new sequence.
Input
First line contains a integer T, means the number of test cases. Each case begin with two integers n, m, means the length of the sequence and the number of queries. Each query contains two lines, first two integers l1, r1, next line two integers l2, r2, l1<=r1 and l2<=r2.
T is about 200.
For 90% of the data, n, m <= 100
For 10% of the data, n, m <= 100000
A[i] fits signed 32-bits int.
Output
For each query, output one line, the median of the query sequence, the answer should be accurate to one decimal point.
Sample Input
4 2
1 2 3 4
1 2
2 4
1 1
2 2
Sample Output
1.5
Problem Idea
解题思路:
【题意】
给你一个已经排好序的n个元素的序列A
从中抽取两个区间([l1,r1]和[l2,r2])的元素组成新的序列
问新序列的中位数是多少
比如样例1,区间[1,2]内的元素为1,2,区间[2,4]内的元素为2,3,4,组成的新序列为1,2,2,3,4,故中位数为2.0
【类型】
分类讨论
【分析】
不清楚别人是怎么做的,不过我的方法有点暴力,写起来有点复杂,但是好理解
因为原序列是排好序的,所以我们组成的新序列只要处理得当,就可以避免因为多次询问而导致多次排序
首先,为了简化选取两个区间的关系,如若遇到l1>l2,那我们就交换这两个区间
这样处理之后,区间关系就只剩下三种:
①
对于这种情况,中位数要么在区间[l1,r1]内,要么在区间[l2,r2]内
我们只需要知道中位数是新序列中的第几个数,然后跟r1-l1+1(区间[l1,r1]内的元素个数)比较一下就可以确定中位数在哪个区间内
②
相交这种情况,无外乎要多判断相交这部分,因为相交部分每个元素会出现两次
③
这种情况其实和第②种情况很类似,处理时注意分区的不同就可以了
另外,对于新序列的元素个数的奇偶性问题,因为偶数个时,中位数是最中间两个数的平均数,所以要多取一个数
那判断方法其实就是再执行一遍之前的分类讨论
代码会给出部分注释以便理解
【时间复杂度&&优化】
O(1)
题目链接→HDU 5857 Median
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1002 Hard problem
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
cjj is fun with math problem. One day he found a Olympic Mathematics problem for primary school students. It is too difficult for cjj. Can you solve it?
Give you the side length of the square L, you need to calculate the shaded area in the picture.
The full circle is the inscribed circle of the square, and the center of two quarter circle is the vertex of square, and its radius is the length of the square.
Input
The first line contains a integer T(1<=T<=10000), means the number of the test case. Each case contains one line with integer l(1<=l<=10000).
Output
For each test case, print one line, the shade area in the picture. The answer is round to two digit.
Sample Input
1
Sample Output
Problem Idea
解题思路:
【题意】
如图,已知正方形边长l,求阴影部分面积(即深灰色部分)
【类型】
计算几何
【分析】
我们都清楚的是,阴影部分面积无法直接计算
只有通过间接方法得到阴影部分面积
如上图蓝色虚线所示作辅助线,点O为圆心,E,F为⊙O与弧BC的两个交点,△AOF的三条边分别为L,L/2,√2/2L
这一切都准备就绪之后,我们就可以开始求解阴影部分面积
我们只需要求出其中一个,那阴影部分面积乘上2就可以了
因为△的三条边都知道了,所以我们可以根据余弦定理求出∠2,∠3,余弦定理如下:
再由定理"三角形的内角和等于180°"求解出∠1
再由定理"三角形的一个外角等于其不相邻的两个内角之和"求解出∠4
之后, 我们根据∠1和长度为L的边AF求解出扇形AEF的面积
再根据∠4和长度为L/2的边OF求解出扇形OEF的面积
那阴影部分面积=2*[扇形OEF-(扇形AEF-△AOF-△AOE)]
三角形面积可以通过海伦公式求得
p=1/2(a+b+c)
S=√(p*(p-a)*(p-b)*(p-c))
【时间复杂度&&优化】
O(1)
题目链接→HDU 5858 Hard problem
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1004 Death Sequence
Accept: 0 Submit: 0
Time Limit: 16000/8000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
You may heard of the Joseph Problem, the story comes from a Jewish historian living in 1st century. He and his 40 comrade soldiers were trapped in a cave, the exit of which was blocked by Romans. They chose suicide over capture and decided that they would form a circle and start killing themselves using a step of three. Josephus states that by luck or maybe by the hand of God, he and another man remained the last and gave up to the Romans.
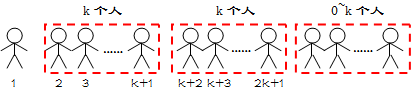
Now the problem is much easier: we have N men stand in a line and labeled from 1 to N, for each round, we choose the first man, the k+1-th one, the 2*k+1-th one and so on, until the end of the line. These poor guys will be kicked out of the line and we will execute them immediately (may be head chop, or just shoot them, whatever), and then we start the next round with the remaining guys. The little difference between the Romans and us is, in our version of story, NO ONE SURVIVES. Your goal is to find out the death sequence of the man.
For example, we have N = 7 prisoners, and we decided to kill every k=2 people in the line. At the beginning, the line looks like this:
1 2 3 4 5 6 7
after the first round, 1 3 5 7 will be executed, we have
2 4 6
and then, we will kill 2 6 in the second round. At last 4 will be executed. So, you need to output 1 3 5 7 2 6 4. Easy, right?
But the output maybe too large, we will give you Q queries, each one contains a number m, you need to tell me the m-th number in the death sequence.
Input
Multiple cases. The first line contains a number T, means the number of test case. For every case, there will be three integers N (1<=N<=3000000), K(1<=K), and Q(1<=Q<=1000000), which indicate the number of prisoners, the step length of killing, and the number of query. Next Q lines, each line contains one number m(1<=m<=n).
Output
For each query m, output the m-th number in the death sequence.
Sample Input
7 2 7
1
2
3
4
5
6
7
Sample Output
3
5
7
2
6
4
Problem Idea
解题思路:
【题意】
n个人排成一行,从第一个人开始,每隔k个人报数,报到数的人被杀死,剩下的人重新排成一行再报数。
一共q个询问,每次询问第m个死的人是谁
n<=3000000,q<=1000000,k>=1
【类型】
递推
【分析】
显然每一轮游戏可以看做是一个子问题
为了方便处理,我们假设n个人的编号为0~n-1,那么编号能被k整除的人则被杀
若某轮中某人的编号为i,如果他在此轮中没有被杀,那么在下轮中编号为i-i/k-1
令s[i]表示前i轮被杀死的总人数,r[i]表示编号为i的人可以存活几轮,p[i]表示编号为i的人在第r[i]+1轮中第几个被杀死
那么我们可以知道,假设当前队伍中还有n个人,那么此轮会有(x-1)/k+1个人被杀死,因为除了第1个人,其余人每k个会死1个
因为我们之前已经假设编号从0开始,所以编号能被k整除的人在此轮就会被杀死,即当i%k==0时,r[i]=0;否则,下一轮该人的编号为i-i/k+1,故r[i]=r[i-i/k-1]+1
这样就可以在O(n)时间内预处理出一个答案序列,那么询问过程O(1)就能完成
【时间复杂度&&优化】
O(n)
题目链接→HDU 5860 Death Sequence
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1005 Road
Accept: 0 Submit: 0
Time Limit: 12000/6000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
There are n villages along a high way, and divided the high way into n-1 segments. Each segment would charge a certain amount of money for being open for one day, and you can open or close an arbitrary segment in an arbitrary day, but you can open or close the segment for just one time, because the workers would be angry if you told them to work multiple period.
We know the transport plan in the next m days, each day there is one cargo need to transport from village ai to village bi, and you need to guarantee that the segments between ai and bi are open in the i-th day. Your boss wants to minimize the total cost of the next m days, and you need to tell him the charge for each day.
(At the beginning, all the segments are closed.)
Input
Multiple test case. For each test case, begins with two integers n, m(1<=n,m<=200000), next line contains n-1 integers. The i-th integer wi(1<=wi<=1000) indicates the charge for the segment between village i and village i+1 being open for one day. Next m lines, each line contains two integers ai,bi(1≤ai,bi<=n,ai!=bi).
Output
For each test case, output m lines, each line contains the charge for the i-th day.
Sample Input
1 2 3
1 3
3 4
2 4
Sample Output
5
5
Problem Idea
解题思路:
【题意】
有n个村庄排成一条直线,相邻两个村庄之间有一条双向路,每条路开放一天需要花费wi的钱
整个过程中,每条路只能开放一次,也就是说一旦某条路关闭,就不能再次开放
每条路一开始都是不开放的
问第m天,为了保证货物能从村庄ai送到村庄bi,需要花费多少钱开放道路
【类型】
线段树(区间更新+单点查询)
【分析】
本人的做法是写了两次线段树,所以代码量有点大,比起别人的会复杂一些,不过我只是多提供一种借鉴罢了
首先,因为每条路只能开放一次,且必须要保证货物能够送达,所以从某条路投入使用的开始到结束,这条路都必须开放着
如样例
村庄2到村庄3这条路,因为第1天用到了,所以必须在第1天开放,虽然第2天没有用到这条路,但是第3天又用到了,所以道路2在第2天是不能关闭的
即便是开着没用,也得开着
所以此题就是找每条路在哪一天开始开放,在哪一天关闭
这个可以通过线段树找每段路的最大天数和最小天数(第1棵线段树)
第1棵线段树的结点表示第几条路
在确定每段路开放的时间区间之后,就可以通过第2棵线段树将每条路的花费进行区间更新
第2棵线段树的结点表示第几天
【时间复杂度&&优化】
O(nlogn)
题目链接→HDU 5861 Road
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1006 Counting Intersections
Accept: 0 Submit: 0
Time Limit: 12000/6000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
Given some segments which are paralleled to the coordinate axis. You need to count the number of their intersection.
The input data guarantee that no two segments share the same endpoint, no covered segments, and no segments with length 0.
Input
The first line contains an integer T, indicates the number of test case.
The first line of each test case contains a number n(1<=n<=100000), the number of segments. Next n lines, each with for integers, x1, y1, x2, y2, means the two endpoints of a segment. The absolute value of the coordinate is no larger than 1e9.
Output
For each test case, output one line, the number of intersection.
Sample Input
4
1 0 1 3
2 0 2 3
0 1 3 1
0 2 3 2
4
0 0 2 0
3 0 3 2
3 3 1 3
0 3 0 2
Sample Output
0
Problem Idea
解题思路:
【题意】
给你n条平行于坐标轴的线段,问它们之间的交点有多少个
【类型】
离散化+树状数组
【分析】
因为题目已经说明所有的线段都是平行于坐标轴的
那么,线段无外乎两种:①平行于x轴;②平行于y轴
那交点必定只有竖向与横向的线段才会产生
另外,此题数据规模显然是不允许我们进行O(n^2)的暴力求解
那我们可以将横向的线段与竖向线段分开处理
对于横向的线段,我们只保留端点
再按x从小到大排序,x相等的情况下,左端点优先于右端点
而竖向的线段同样按x从小到大排序,但是不拆分成两个端点,而是保留整条线段
然后枚举竖向线段,将小于该竖向线段横坐标的所有点进行处理
若点为左端点,则在其对应的值处的树状数组做+1操作,若为右端点,则做-1操作
这保证了对于第i条竖向线段,当前树状数组中记录了横坐标横跨该竖向线段的线段数量
当然,这些做法的前提是一开始已对坐标离散化,不然过于分散的坐标,即便树状数组也避免不了TLE的命运
此题可能理解起来比较绕,不过只要理解了,就会觉得一切都是水到渠成的
好了,具体看代码,不懂提问
【时间复杂度&&优化】
O(nlogn)
题目链接→HDU 5862 Counting Intersections
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1011 Water problem
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3+3+5+4+4=19 letters used in total.If all the numbers from 1 to n (up to one thousand) inclusive were written out in words, how many letters would be used?
Do not count spaces or hyphens. For example, 342 (three hundred and forty-two) contains 23 letters and 115 (one hundred and fifteen) contains 20 letters. The use of "and" when writing out numbers is in compliance with British usage.
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases.
For each test case: There is one positive integer not greater one thousand.
Output
For each case, print the number of letters would be used.
Sample Input
1
2
3
Sample Output
6
11
Problem Idea
解题思路:
【题意】
求整数1~n表示成英文单词之后共有多少个英文字母组成(不包含空格和连接符'-')
如342,其英文表示为three hundred and forty-two,共包含23个英文字母(three有5个字母,hundred有7个字母,and有3个字母,forty有5个字母,two有3个字母,共计5+7+3+5+3=23)
【类型】
模拟
【分析】
这题显然是细节题
一个考虑不周,就会导致计算错误,所以我们不急着求解,而是先观察
one
two
three
four
five
six
seven
eight
nine
ten
eleven
twelve
thirteen
fourteen
fifteen
sixteen
seventeen
eighteen
nineteen
twenty
twenty-one
twenty-two
twenty-three
twenty-four
twenty-five
twenty-six
twenty-seven
twenty-eight
twenty-nine
thirty
thirty-one
thirty-two
thirty-three
thirty-four
thirty-five
thirty-six
thirty-seven
thirty-eight
thirty-nine
forty
forty-one
forty-two
forty-three
forty-four
forty-five
forty-six
forty-seven
forty-eight
forty-nine
fifty
fifty-one
fifty-two
fifty-three
fifty-four
fifty-five
fifty-six
fifty-seven
fifty-eight
fifty-nine
sixty
sixty-one
sixty-two
sixty-three
sixty-four
sixty-five
sixty-six
sixty-seven
sixty-eight
sixty-nine
seventy
seventy-one
seventy-two
seventy-three
seventy-four
seventy-five
seventy-six
seventy-seven
seventy-eight
seventy-nine
eighty
eighty-one
eighty-two
eighty-three
eighty-four
eighty-five
eighty-six
eighty-seven
eighty-eight
eighty-nine
ninety
ninety-one
ninety-two
ninety-three
ninety-four
ninety-five
ninety-six
ninety-seven
ninety-eight
ninety-nine
one hundred
101 one hundred and one
102 one hundred and two
103 one hundred and three
104 one hundred and four
105 one hundred and five
106 one hundred and six
107 one hundred and seven
108 one hundred and eight
109 one hundred and nine
120 one hundred and twenty
199 one hundred and ninety-nine
999 nine hundred and ninety-nine
1000 one thousand
由上述数据可以分析,1~19很特殊,所以我们可以先存下每个数转化成英文单词后的字母个数
而20~99这部分,每个数的个位都是0~9,这个我们已经存好了,所以只需要记录一下十位数转化为单词后的字母个数
至于100~999这部分,它后两位数是1~99,这个我们之前已经统计好了,只要再加上百位1~9和"and"、"hundred"的字母个数即可
当然,整百的话由于没有"and",所以特别注意不要多加
1000的话另外记录就可以了
此题其实是没有难度的,难就难在处理的时候不小心会出错
【时间复杂度&&优化】
O(1)
题目链接→HDU 5867 Water problem
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include