6.10力扣 10号出去逛街了,11号补上! 打印n位数
class Solution:
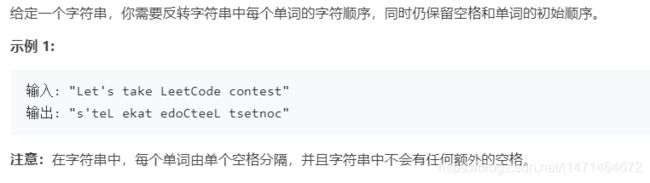
def reverseWords(self, s: str) -> str:
arr=s.split(' ')
res=[]
for i in arr:
res.append(i[::-1])
return ' '.join(res)
class Solution:
def reverseVowels(self, s: str) -> str:
lis=['a','e','i','o','u','A','E','I','O','U']
s=list(s)
i,j=0,len(s)-1
while i<j:
if s[i] not in lis:
i+=1
if s[j] not in lis:
j-=1
if s[i] in lis and s[j] in lis:
s[i],s[j]=s[j],s[i]
i+=1
j-=1
return ''.join(s)
class Solution:
def findMin(self, nums: List[int]) -> int:
if nums[0]<nums[-1]:
return nums[0]
left,right=0,len(nums)-1
while left<right:
mid=left+(right-left)//2
#小于右端点,mid可能为最小值
if nums[mid]<nums[right]:
right=mid
else:
#大于右端点,mid一定不是最小值
left=mid+1
return nums[left]
154. 寻找旋转排序数组中的最小值 II
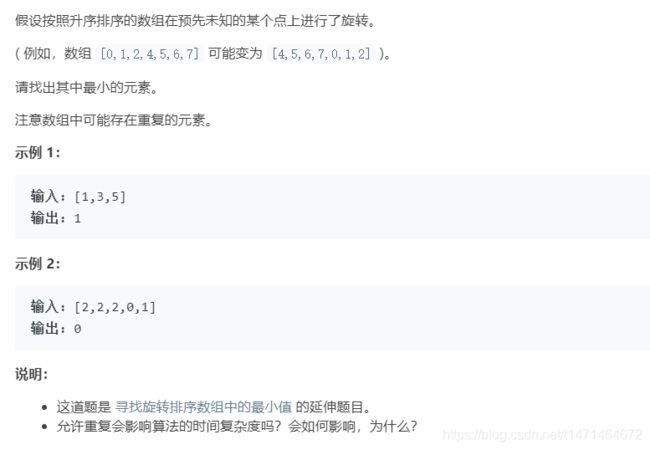
为什么要用nums[mid]和nums[r]比较,而不是和nums[l]比较?
因为是寻找最小值,看如下例子:
[1,2,3,4,5]
[2,3,4,5,1]
虽然nums[mid]都大于nums[l],但是最小值可以在左侧或者右侧

将中轴元素与右边界元素作比较
1)中轴元素小于右边界元素,中轴元素跟右边界元素在 同一半边 。这时候最小元素在中轴元素 左边 (也有可能是中轴元素),将右边界指针移动到中轴元素位置(high = pivot)。
2)中轴元素大于右边界元素,中轴元素和左边界元素在一边,最小元素在中轴元素右边,下届指针移动到中轴元素位置右边(low = pivot + 1)
3)中轴元素等于右边界元素,能确定最小元素在中轴元素的左边还是右边。
为了缩小查找范围,安全的方法是将右边界指针减一(high = high - 1)。
上述策略可以有效地避免死循环,同时可以保证永远不会跳过最小元素

class Solution:
def findMin(self, nums: List[int]) -> int:
left,right=0,len(nums)-1
while left<right:
mid=left+(right-left)//2
if nums[mid]<nums[right]:
right=mid
elif nums[mid]>nums[right]:
left=mid+1
else:
right=right-1
return nums[left]
class Solution:
def translateNum(self, num: int) -> int:
s=str(num)
n=len(s)
dp=[0]*(n+1)
dp[0]=1
dp[1]=1
for i in range(2,n+1):
if s[i-2:i]<='25' and s[i-2:i]>='10':
dp[i]=dp[i-1]+dp[i-2]
else:
dp[i]=dp[i-1]
return dp[-1]
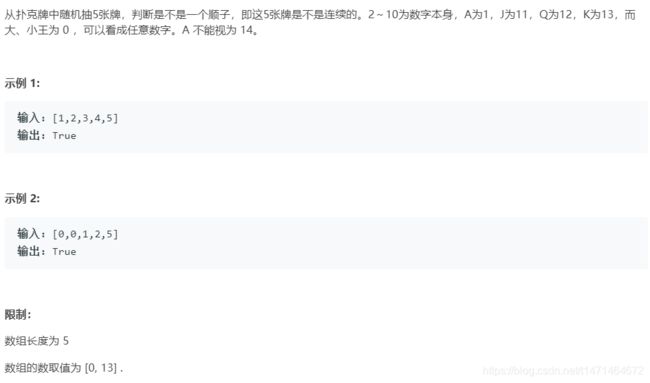
class Solution:
def isStraight(self, nums: List[int]) -> bool:
ma,mi=0,14
match=set()
for i in nums:
if i==0:
continue
ma=max(ma,i)
mi=min(mi,i)
if i in match:
return False
match.add(i)
return ma-mi<5
面试题60. n个骰子的点数
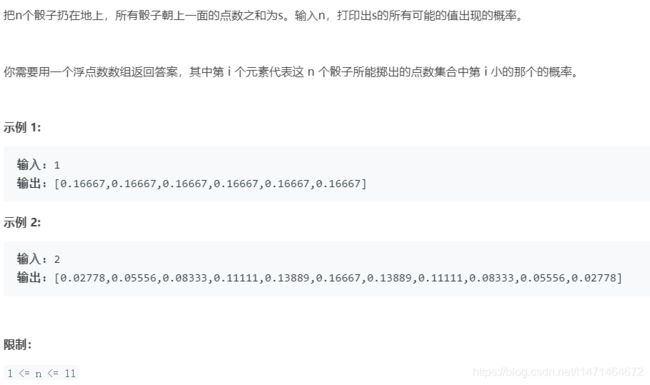
n个骰子可以得到n-6*n的点数
本轮点数之和为k出现次数等于上一轮点数的和为k-1,k-2,k-3,k-4,k-5,k-6出现的次数之和。
初始化,n=1时,出现点数有1,2,3,4,5,6,次数都为1
class Solution:
def twoSum(self, n: int) -> List[float]:
#n个骰子的点数和为 n-6*n
#dp[i][j]:I个骰子的点数和为J的次数
dp=[[0 for i in range(6*n+1)] for j in range(n+1)]
for i in range(1,7):
dp[1][i]=1
#骰子数
for i in range(2,n+1):
#点数和
for j in range(i,6*i+1):
for k in range(1,7):
if j-k>=0:
dp[i][j]+=dp[i-1][j-k]
res=[]
for i in range(n,6*n+1):
res.append(dp[n][i]*1.0/6**n)
return res
628. 三个数的最大乘积

最大值:正数的三个最大值的乘积,存在负数时 两个负数最小值乘积乘以正数最大值,全是负数也是最大的三个负数乘积最大
class Solution:
def maximumProduct(self, nums: List[int]) -> int:
res=1
if len(nums)<=3:
for i in nums:
res*=i
return res
#最大,次大,三大
a,b,c=float('-inf'),float('-inf'),float('-inf')
#最小,次小
m,n=float('inf'),float('inf')
for i in nums:
if i<=m:
m,n=i,m
elif i<=n:
n=i
if i>=a:
a,b,c=i,a,b
elif i>=b:
b,c=i,b
elif i>=c:
c=i
return max(a*b*c,m*n*a)
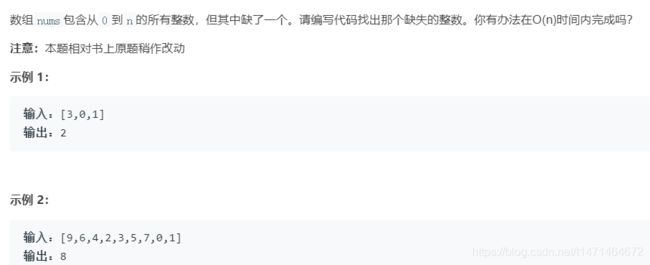
class Solution:
def missingNumber(self, nums: List[int]) -> int:
res=0
for i in range(len(nums)):
res^=i
res^=nums[i]
return res^len(nums)
class Solution:
def printNumbers(self, n: int) -> List[int]:
res=[]
for i in range(1,10**n):
res.append(i)
return res
class Solution:
def printNumbers(self, n: int) -> [int]:
def dfs(x):
if x == n:
s = ''.join(num[self.start:])
if s != '0': res.append(int(s))
if n - self.start == self.nine: self.start -= 1
return
for i in range(10):
if i == 9: self.nine += 1
num[x] = str(i)# 固定第 x 位为 i
dfs(x + 1)# 开启固定第 x + 1 位
self.nine -= 1
num, res = ['0'] * n, []# 起始数字定义为 n 个 0 组成的字符列表
self.nine = 0 #
self.start = n - 1
dfs(0)# 开启全排列递归
return res