1、特殊值法
特值可以一个特殊数、也可以是一些特殊式子,它借助于“特殊性存在于一般性之中”这个哲学原理。通过特值开道,使看上去很难进行一般性求解的问题,在特值的“作用”下产生结论。
例1、设函数![]() 在R上的导函数为
在R上的导函数为![]() ,且
,且![]() ,下面的不等式在R内恒成立的是
,下面的不等式在R内恒成立的是
A、![]()
B、![]()
C、![]()
D、![]()
解析:首先令![]() ,得
,得![]() ,于是,排除B,D。
,于是,排除B,D。
再令![]() ,显然,
,显然,![]() 满足题设条件,此时,
满足题设条件,此时,![]() 不一定大于零,即选项C并非在R内恒成立,于是也被排除。故选A。
不一定大于零,即选项C并非在R内恒成立,于是也被排除。故选A。
例2、已知函数![]() 是定义在实数集
是定义在实数集![]() 上的不恒为零的偶函数,且对任意实数
上的不恒为零的偶函数,且对任意实数![]() 都有
都有![]() ,则
,则![]() 的值是
的值是
A.0
B.![]()
C.1
D.![]()
解析:令![]() ,得
,得![]() ,结合
,结合![]() 是定义在实数集
是定义在实数集![]() 上的不恒为零的偶函数,得
上的不恒为零的偶函数,得![]() ;再令
;再令![]() ,得
,得![]()
2、构造方程法
方程思想是重要的数学思想,方程与函数又是一对“密友”,函数中藏着方程、方程里含着函数是常有的事。遇到递推或含有明显变量的式子,想一想方程是应该的,也许它引领你层层深入,最终产生结论。
A.-1
B.0
C.1
D.2
解析:由![]() ,得
,得![]() 两式相加得
两式相加得![]() ,显然
,显然![]()
那么![]() ,选C。
,选C。
例4、已知函数![]() 在R上满足
在R上满足![]() ,则曲线
,则曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是
(A)![]()
(B)![]()
(C)![]()
(D)![]()
解析:由![]() 得
得![]() ,
,
即![]() ,消去
,消去![]() 得
得![]() ∴
∴![]() ,∴切线方程为
,∴切线方程为![]() ,即
,即![]() 选A
选A
3、数形结合法
“数少形时缺直观,形少数时难入微”它准确的告诉我们:数形结合,相得益彰;利用数、式进行深入细致的分析;利用图形直观又可以看出数、式的内在关系。
B、![]()
C、![]()
D、![]()
解析:作出![]() 的图像,如右图
的图像,如右图
由图像可知![]() 在定义域内是增函数
在定义域内是增函数
于是,由![]() 得
得![]()
![]()
故选择C。
例6、若![]() 满足
满足![]() ,
, ![]() 满足
满足![]() ,
, ![]() +
+![]() =
=
(A)![]()
(B)3
(C) ![]()
(D)4
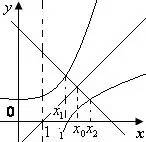
再令![]() ,则
,则![]() 两函数
两函数![]() 图像交点的横坐标。
图像交点的横坐标。
由于![]() 与
与![]() 的图像关于
的图像关于![]() 对称,
对称,
4、抓不变量解题
一个看似复杂的问题,细心观察之后,也许可以发现其中不变的东西,此时,我们可以建立在这些“不变”的基础上,以静制动。
B.![]() 或
或![]()
D.![]() 或
或![]()
解析:设过![]() 的直线与
的直线与![]() 相切于点
相切于点![]() ,所以切线方程为
,所以切线方程为![]() ,即
,即![]() ,又
,又![]() 在切线上,则
在切线上,则![]() 或
或![]() ,当
,当![]() 时,由
时,由![]() 与
与![]() 相切可得
相切可得![]() ,当
,当![]() 时,由
时,由![]() 与
与![]() 相切可得
相切可得![]() ,所以选
,所以选![]() .
.
例8、设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,则曲线
,则曲线![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为
A.![]()
B.![]()
C.![]()
D.![]()
解析:由已知![]() ,而
,而![]() ,所以
,所以![]() 故选A。
故选A。
5、特征法
特征,是一事物区别于它事物的本质,抓住特征,就等于抓住了本质。面对图形问题,我们要认真观察、仔细分析,也许一、两个特征就是“破”题的关键。
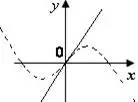
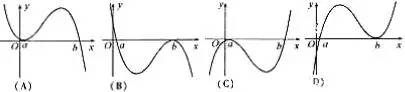
例9、设![]() <b,函数
<b,函数![]() 的图像可能是
的图像可能是
解析:看看函数式,可以发现![]() 时,
时,![]() ,再看图形特征,立即排除A、B;再看
,再看图形特征,立即排除A、B;再看![]() 时,
时,![]() ,再看图形,排除D,于是选C。
,再看图形,排除D,于是选C。
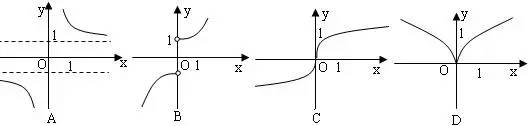
解析:首先由函数的定义域可得![]() ,看看图形,立即排除C、D。再由
,看看图形,立即排除C、D。再由![]() 即函数递减,选A。
即函数递减,选A。
6、替换法
替换,是一种策略,它可以变生疏为熟悉、变复杂为简单、变抽象为具体;当我们面对抽象、复杂问题时,若能灵活替换,可以说:攻防自如。
例11、函数![]() 的定义域为R,若
的定义域为R,若![]() 与
与![]() 都是奇函数,则( )
都是奇函数,则( )
(A)![]() 是偶函数
是偶函数
(B)![]() 是奇函数
是奇函数
(C)![]()
(D)![]() 是奇函数
是奇函数
由![]()
![]()
即![]() 是奇函数。故选D
是奇函数。故选D
例12、已知定义在R上的奇函数![]() ,满足
,满足![]() ,且在区间[0,2]上是增函数,则( ).
,且在区间[0,2]上是增函数,则( ).
A.![]()
B.![]()
C.![]()
D.![]()
解析:因为![]() 满足
满足![]()
![]() ,所以函数是以8为周期的周期函数, 则
,所以函数是以8为周期的周期函数, 则![]() ,
,![]() ,
,![]() ,又因为
,又因为![]() 在R上是奇函数,
在R上是奇函数, ![]() ,得
,得![]() ,
,![]() ,而由
,而由![]() 得
得![]() ,又因为
,又因为![]() 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以![]() ,所以
,所以![]() ,即
,即![]() ,故选D.
,故选D.
7、最值法
最值是函数的重要特征量,很多命题人总是喜欢在此处作文章。请看:
例13、设函数![]() 在(
在(![]() ,+
,+![]() )内有定义。对于给定的正数K,定义函数
)内有定义。对于给定的正数K,定义函数![]() 取函数
取函数![]() 。若对任意的
。若对任意的![]() ,恒有
,恒有![]() =
=![]() ,则
,则
A.K的最大值为2
B. K的最小值为2
C.K的最大值为1
D. K的最小值为1
解析:由![]() 知
知![]() ,所以
,所以![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 即
即![]() 的值域是
的值域是![]() ,而要使
,而要使![]() 在
在![]() 上恒成立,则必有
上恒成立,则必有![]() ,于是
,于是![]() 。故选D项。
。故选D项。
例14、把函数![]() 的图像
的图像![]() 向右平移
向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后得到图像
个单位长度后得到图像![]() .若对任意的
.若对任意的![]() ,曲线
,曲线![]() 与
与![]() 至多只有一个交点,则
至多只有一个交点,则![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
解析:设曲线![]() 的解析式为
的解析式为![]()
则方程![]() ,即
,即![]() ,即
,即![]() 对任意
对任意![]() 恒成立,于是
恒成立,于是![]() 的最大值,令
的最大值,令![]() 则
则![]() 由此知函数
由此知函数![]() 在(0,2)上为增函数,在
在(0,2)上为增函数,在![]() 上为减函数,所以当
上为减函数,所以当![]() 时,函数
时,函数![]() 取最大值,即为4,于是
取最大值,即为4,于是![]() 。
。
8.本质法
“万变不离其宗”,不论如何创新,本质的东西是改不了的。近年试题的创新力度大、新题层出不穷,当我们遇到创新问题时,一定要注意抓住本质,以本质为切入点,也许创新题就不是那么难了。
例15、对于正实数![]() ,记
,记![]() 为满足下述条件的函数
为满足下述条件的函数![]() 构成的集合:
构成的集合:![]() 且
且![]() ,有
,有![]() .下列结论中正确的是 ( )
.下列结论中正确的是 ( )
A.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,则
,则![]() 21世纪教育网
21世纪教育网
D.若![]() ,
,![]() ,且
,且![]() ,则
,则![]()
例16、设函数![]() 的定义域为
的定义域为![]() ,若所有点
,若所有点![]() 构成一个正方形区域,则
构成一个正方形区域,则![]() 的值为
的值为
A.![]()
B.![]()
C.![]()
D.不能确定
我为大家整理了高中的一些干货资料,能轻松提高50分
![]()
关注公众![]() 号高中生学习资料库,回复:“2345”,
号高中生学习资料库,回复:“2345”,
即可免费领取噢!