Nastya and Scoreboard

Denis, after buying flowers and sweets (you will learn about this story in the next task), went to a date with Nastya to ask her to become a couple. Now, they are sitting in the cafe and finally… Denis asks her to be together, but … Nastya doesn’t give any answer.

The poor boy was very upset because of that. He was so sad that he punched some kind of scoreboard with numbers. The numbers are displayed in the same way as on an electronic clock: each digit position consists of $7$ segments, which can be turned on or off to display different numbers. The picture shows how all $10$ decimal digits are displayed:

After the punch, some segments stopped working, that is, some segments might stop glowing if they glowed earlier. But Denis remembered how many sticks were glowing and how many are glowing now. Denis broke exactly $k$ segments and he knows which sticks are working now. Denis came up with the question: what is the maximum possible number that can appear on the board if you turn on exactly $k$ sticks (which are off now)?

It is allowed that the number includes leading zeros.

Input

The first line contains integer $n(1\le n\le 2000)$ — the number of digits on scoreboard and $k(0\le k\le 2000)$ — the number of segments that stopped working.

The next $n$ lines contain one binary string of length $7$, the $i$-th of which encodes the $i$-th digit of the scoreboard.

Each digit on the scoreboard consists of $7$ segments. We number them, as in the picture below, and let the $i$-th place of the binary string be $0$ if the $i$-th stick is not glowing and $1$ if it is glowing. Then a binary string of length $7$ will specify which segments are glowing now.

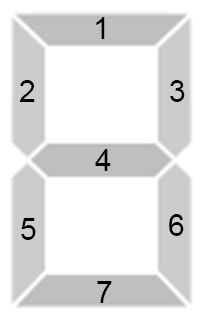
Thus, the sequences “1110111”, “0010010”, “1011101”, “1011011”, “0111010”, “1101011”, “1101111”, “1010010”, “1111111”, “1111011” encode in sequence all digits from 0 to 9 inclusive.

Output

Output a single number consisting of $n$ digits — the maximum number that can be obtained if you turn on exactly $k$ sticks or $-1$, if it is impossible to turn on exactly $k$ sticks so that a correct number appears on the scoreboard digits.

Examples

input
1 7 0000000
output
8

input
2 5 0010010 0010010
output
97

input
3 5 0100001 1001001 1010011
output
-1

Note

In the first test, we are obliged to include all $7$ sticks and get one 8 digit on the scoreboard.

In the second test, we have sticks turned on so that units are formed. For $5$ of additionally included sticks, you can get the numbers $07,18,34,43,70,79,81$ and $97$, of which we choose the maximum — $97$.

In the third test, it is impossible to turn on exactly $5$ sticks so that a sequence of numbers appears on the scoreboard.

题意：已知将0-9每个数字按照电子表格式按照字符串表示出来，给出n个字符串和k个灯管，将这k个灯管(相当于字符串中的1)全部放入n个字符串中，可以构成的最大数字为多少(数字按照字符串顺序)，允许有前置零.

思路：

1. 首先要构成最大数字，贪心策略+dfs，优先考虑每一个字符串转化成最大数字
2. 统计每一个字符串转化成0-9分别需要多少个灯管
3. 剪枝优化步骤，首先灯管中间使用超过k剪掉，灯管最后没有恰好使用k个减掉
4. 剩下的字符串转换成数字需要的最少灯管多于已知灯管，或者需要的最多灯管少于已知灯管，都可以剪枝
5. 这个时候还是会T，我们引入$dp$记忆化数组，$dp[现在第几个字符串][用了多少灯管]$表示当前状态能否恰好使用k个灯管，这样可以减少许多循环
6. 具体见代码详解

代码如下：

#include
#include
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;
const int mx=2e3+20;
int dp[mx][mx],cnt[mx][10];//dp记忆化数组，cnt表示第i个字符串转化为数字j需要的灯管数量
int minn[mx],maxn[mx];//分别为剩下字符串转化为数字需要的最少、最多灯管
char s[mx][10],c[mx][10];//输入字符串数组，辅助统计数组
int n,k;
vector<int>p;//记录结果数组

void init()
{
	strcpy(c[0],"-1110111");
	strcpy(c[1],"-0010010");
	strcpy(c[2],"-1011101");
	strcpy(c[3],"-1011011");
	strcpy(c[4],"-0111010");
	strcpy(c[5],"-1101011");
	strcpy(c[6],"-1101111");
	strcpy(c[7],"-1010010");
	strcpy(c[8],"-1111111");
	strcpy(c[9],"-1111011");
	memset(dp,-1,sizeof(dp));//-1表示还没有判断
	memset(cnt,0,sizeof(cnt));
	memset(minn,0,sizeof(minn));
	memset(maxn,0,sizeof(maxn));
	p.clear();
	
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=9;j++)
		{
			for(int k=1;k<=7;k++)
			{
				if(s[i][k]=='0'&&c[j][k]=='1')//由0变为1需要一个灯管
				cnt[i][j]++;
				else if(s[i][k]=='1'&&c[j][k]=='0')//由1无法变为0，直接break
				{
					cnt[i][j]=-1;
					break;
				}
			}
		}
    }
    
    for(int i=n;i>=1;i--)
    {
    	int l=10,r=0;
    	for(int j=0;j<=9;j++)
    	{
    		if(cnt[i][j]>=0)
    		{
    			l=min(l,cnt[i][j]);
    			r=max(r,cnt[i][j]);
    		}
    	}
    	minn[i]=minn[i+1]+l;//记录最少
    	maxn[i]=maxn[i+1]+r;
    }
}

int dfs(int now,int cur)
{
	if((cur>k)||(k-cur<minn[now])||(k-cur>maxn[now]))//剪枝
	return 0;

    if(dp[now][cur]!=-1)//如果已经判断了剩下能够转化完成，直接返回状态
    return dp[now][cur];
	if(n+1==now)
	{
		if(cur==k)
		return 1;
		return 0;
	}
	
	for(int i=9;i>=0;i--)
	{
		if(cnt[now][i]>=0)
		{
			if(dfs(now+1,cur+cnt[now][i]))
			{
				p.push_back(i);
				return dp[now][cur]=1;//1状态表示可以转化
			}
		}
	}
	dp[now][cur]=0;//0状态表示无法转化
	return 0;
}
	
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++)
	scanf("%s",s[i]+1);
	
	init();
	
	dfs(1,0);
	
	if(p.size()==0)
	printf("-1\n");
	else
	{
		for(int i=p.size()-1;i>=0;i--)
		printf("%d",p[i]);
	}
	return 0;
}