正睿集训每日总结【7.28】
目录
- 期望与概率
- 基本概念
- 常用公式
- 拿球问题
- 游走问题
- 经典问题
期望与概率
基本概念
1、随机变量:有多种可能的取值的变量。
2、 P ( A ) P(A) P(A) :事件A发生的概率。
3、 E ( X ) E(X) E(X) :随机变量 X X X 的期望值,公式: E ( X ) = ∑ P ( x = i ) ∗ i E(X)=\sum P(x=i)*i E(X)=∑P(x=i)∗i或者我们可以看一下度娘定义:
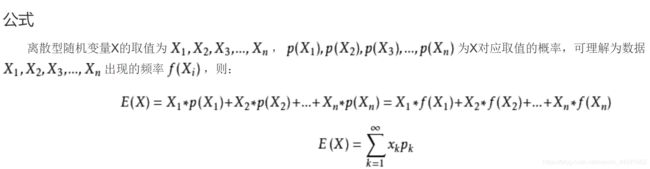
4、独立事件:互不影响的事件,满足: P ( A B ) = P ( A ) P ( B ) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ① E ( A B ) = E ( A ) E ( B ) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ② P(AB)=P(A)P(B)··········①\\ E(AB)=E(A)E(B)··········② P(AB)=P(A)P(B)⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅①E(AB)=E(A)E(B)⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅②对于②式,我们可以证明一下: E ( A B ) = ∑ i = 1 ∞ ∑ j = 1 ∞ P ( i = A 且 j = B ) ∗ i ∗ j = ∑ i = 1 ∞ P ( i = A ) ∗ i ∗ ∑ j = 1 ∞ P ( j = B ) ∗ j = E ( A ) ∗ E ( B ) \begin{aligned} E(AB)&=\sum_{i=1}^\infty\sum_{j=1}^\infty P(i=A且j=B)*i*j\\ &=\sum_{i=1}^\infty P(i=A)*i*\sum_{j=1}^\infty P(j=B)*j\\ &=E(A)*E(B) \end{aligned} E(AB)=i=1∑∞j=1∑∞P(i=A且j=B)∗i∗j=i=1∑∞P(i=A)∗i∗j=1∑∞P(j=B)∗j=E(A)∗E(B)证毕。
常用公式
1、当 − 1 < x < 1 -1<x<1 −1<x<1 时(当然,概率题中 x > 0 x>0 x>0 ),有: ∑ i = 0 ∞ x i = 1 1 − x \sum_{i=0}^\infty x^i=\frac 1{1-x} ∑i=0∞xi=1−x1
2、 ∑ i = 0 n x i = 1 − x n + 1 1 − x \sum_{i=0}^n x^i=\frac{1-x^{n+1}}{1-x} ∑i=0nxi=1−x1−xn+1
对于第 1 1 1 条我们可以用第 2 2 2 条证明: 当 n → ∞ 时 , ∵ 0 < x < 1 ∴ lim n → ∞ x n + 1 = 0 ∴ ∑ i = 0 ∞ x i = lim n → ∞ ∑ i = 0 n x i = lim n → ∞ 1 − x n + 1 1 − x = 1 1 − x \begin{aligned} &当n\to\infty时,\\ &\because 0<x<1\\ &\therefore\lim_{n\to\infty}x^{n+1}=0\\ &\therefore\sum_{i=0}^\infty x^i=\lim_{n\to\infty}\sum_{i=0}^n x^i\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\lim_{n\to\infty}\frac{1-x^{n+1}}{1-x}\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac 1{1-x} \end{aligned} 当n→∞时,∵0<x<1∴n→∞limxn+1=0∴i=0∑∞xi=n→∞limi=0∑nxi =n→∞lim1−x1−xn+1 =1−x1证毕。
3、期望的线性性: E ( X + Y ) = E ( X ) + E ( Y ) E(X+Y)=E(X)+E(Y) E(X+Y)=E(X)+E(Y)
Tip:它对任意 X , Y X,Y X,Y 均成立。
证明: E ( X + Y ) = ∑ i ∑ j P ( X = i 且 Y = j ) ∗ ( i + j ) = ∑ i ∑ j P ( X = i 且 Y = j ) ∗ i + ∑ i ∑ j P ( X = i 且 Y = j ) ∗ j 而 ∑ i ∑ j P ( X = i 且 Y = j ) ∗ i = ∑ i P ( X = i ) ∗ i = E ( X ) 同 理 , ∑ i ∑ j P ( X = i 且 Y = j ) ∗ j = ∑ j P ( Y = j ) ∗ j = E ( Y ) ∴ E ( X + Y ) = E ( X ) + E ( Y ) \begin{aligned} &E(X+Y)=\sum_i\sum_j P(X=i且Y=j)*(i+j)\\ &\qquad\qquad\ \ =\sum_i\sum_j P(X=i且Y=j)*i+\sum_i\sum_j P(X=i且Y=j)*j\\ &而\sum_i\sum_j P(X=i且Y=j)*i=\sum_i P(X=i)*i=E(X)\\ &同理,\sum_i\sum_j P(X=i且Y=j)*j=\sum_j P(Y=j)*j=E(Y)\\ &\therefore E(X+Y)=E(X)+E(Y) \end{aligned} E(X+Y)=i∑j∑P(X=i且Y=j)∗(i+j) =i∑j∑P(X=i且Y=j)∗i+i∑j∑P(X=i且Y=j)∗j而i∑j∑P(X=i且Y=j)∗i=i∑P(X=i)∗i=E(X)同理,i∑j∑P(X=i且Y=j)∗j=j∑P(Y=j)∗j=E(Y)∴E(X+Y)=E(X)+E(Y)证毕。
★4、前缀和技巧: P ( X = K ) = P ( X ⩽ K ) − P ( X ⩽ ( K − 1 ) ) 或 者 P ( X = K ) = P ( X ⩾ K ) − P ( X ⩾ ( K + 1 ) ) P(X=K)=P(X\leqslant K)-P(X\leqslant(K-1))\\ 或者\\ P(X=K)=P(X\geqslant K)-P(X\geqslant (K+1)) P(X=K)=P(X⩽K)−P(X⩽(K−1))或者P(X=K)=P(X⩾K)−P(X⩾(K+1))★5、概率为 p p p 的事件期望 1 p \frac 1 p p1 次后发生。 设 次 数 为 x 那 么 问 题 就 等 价 于 证 明 E ( x ) = 1 p E ( x ) = ∑ i = 1 ∞ P ( x = i ) ∗ i P ( x = i ) = P ( x ⩾ i ) − P ( x ⩾ ( i + 1 ) ) = ( 1 − p ) i − 1 − ( 1 − p ) i ∴ 原 式 = ∑ i = 1 ∞ ( ( 1 − p ) i − 1 − ( 1 − p ) i ) ∗ i = ∑ i = 0 ∞ ( 1 − p ) − i = 1 1 − ( 1 − p ) = 1 p \begin{aligned} &设次数为 x\\ &那么问题就等价于证明E(x)=\frac1 p\\ &E(x)=\sum_{i=1}^\infty P(x=i)*i\\ &P(x=i)=P(x\geqslant i)-P(x\geqslant(i+1))=(1-p)^{i-1}-(1-p)^i\\ &\therefore 原式=\sum_{i=1}^\infty((1-p)^{i-1}-(1-p)^i)*i\\ &\qquad\quad\ =\sum_{i=0}^\infty(1-p)^{-i}\\ &\qquad\quad\ =\frac 1{1-(1-p)}\\ &\qquad\quad\ =\frac 1 p \end{aligned} 设次数为x那么问题就等价于证明E(x)=p1E(x)=i=1∑∞P(x=i)∗iP(x=i)=P(x⩾i)−P(x⩾(i+1))=(1−p)i−1−(1−p)i∴原式=i=1∑∞((1−p)i−1−(1−p)i)∗i =i=0∑∞(1−p)−i =1−(1−p)1 =p1证毕。
6、有 n n n 个随机变量 X [ 1 ∼ n ] X[1\sim n] X[1∼n] ,每个随机变量都是从 1 ∼ S 1\sim S 1∼S 中随机⼀个整数,求 m a x ( X [ 1 ∼ n ] ) max(X[1\sim n]) max(X[1∼n]) 的期望。 E ( y ) = ∑ i P ( y = i ) ∗ i = ∑ i ( P ( y ⩽ i ) − P ( y ⩽ ( i − 1 ) ) ) ∗ i = ∑ i ( ( i s ) n − ( i − 1 s ) n ) ∗ i \begin{aligned} E(y)&=\sum_i P(y=i)*i\\ &=\sum_i (P(y\leqslant i)-P(y\leqslant (i-1)))*i\\ &=\sum_i ((\frac i s)^n-(\frac{i-1}s)^n)*i \end{aligned} E(y)=i∑P(y=i)∗i=i∑(P(y⩽i)−P(y⩽(i−1)))∗i=i∑((si)n−(si−1)n)∗i
总结:前缀和技巧是十分常用的,也很巧妙,要好好利用。
拿球问题
1、箱子里有 n n n 个球 1 ∼ n 1\sim n 1∼n ,你要从里面拿 m m m 次球,拿了后不放回,求取出的数字之和的期望。
2、箱子里有 n n n 个球 1 ∼ n 1\sim n 1∼n ,你要从里面拿 m m m 次球,拿了后放回,求取出的数字之和的期望。
3、箱子里有 n n n 个球 1 ∼ n 1\sim n 1∼n ,你要从里面拿 m m m 次球,拿了后以 p 1 p_1 p1 的概率放回,以 p 2 p_2 p2 的概率放回两个和这个相同的球,求取出的数字之和的期望。
其实这三个问题答案都一样,因为总体上看每个球都是一样的。 E ( S ) = ∑ i E ( x i ) = E ( ∑ i y i ∗ i ) = ∑ i E ( y i ∗ i ) = ∑ i E ( y i ) ∗ ∑ i E ( i ) = m ∗ ∑ i E ( i ) = m ∗ ( n + 1 ) 2 \begin{aligned} E(S)&=\sum_i E(x_i)\\ &=E(\sum_i y_i*i)\\ &=\sum_i E(y_i*i)\\ &=\sum_i E(y_i)*\sum_i E(i)\\ &=m*\sum_i E(i)\\ &=\frac{m*(n+1)}2 \end{aligned} E(S)=i∑E(xi)=E(i∑yi∗i)=i∑E(yi∗i)=i∑E(yi)∗i∑E(i)=m∗i∑E(i)=2m∗(n+1)
总结:对于某些概率问题,我们要从总体上看,不要被局部限制了思维。
游走问题
1、在一条 n n n 个点的链上游走,求从一端走到另一端的期望步数。
设 x i 表 示 随 机 游 走 从 i 第 一 次 走 到 i + 1 的 步 数 y = ∑ i = 1 n − 1 x i E ( y ) = ∑ i = 1 n − 1 E ( x i ) ∵ E ( x 2 ) = 1 2 + 1 2 ∗ ( 1 + E ( x 1 ) + E ( x 2 ) ) ∴ E ( x i ) = 1 2 + 1 2 ∗ ( 1 + E ( x i − 1 ) + E ( x i ) ) = E ( x i − 1 ) + 2 ∴ E ( y ) = ∑ i = 1 n − 1 E ( x i ) = 1 + 3 + 5 + 7 + … = ( n − 1 ) 2 \begin{aligned} &设x_i表示随机游走从i第一次走到i+1的步数\\ &y=\sum_{i=1}^{n-1}x_i\\ &E(y)=\sum_{i=1}^{n-1}E(x_i)\\ &\because E(x_2)=\frac 1 2+\frac 1 2*(1+E(x_1)+E(x_2))\\ &\therefore E(x_i)=\frac 1 2+\frac 1 2*(1+E(x_{i-1})+E(x_i))=E(x_{i-1})+2\\ &\therefore E(y)=\sum_{i=1}^{n-1}E(x_i)=1+3+5+7+…=(n-1)^2 \end{aligned} 设xi表示随机游走从i第一次走到i+1的步数y=i=1∑n−1xiE(y)=i=1∑n−1E(xi)∵E(x2)=21+21∗(1+E(x1)+E(x2))∴E(xi)=21+21∗(1+E(xi−1)+E(xi))=E(xi−1)+2∴E(y)=i=1∑n−1E(xi)=1+3+5+7+…=(n−1)22、在一张 n n n 个点的完全图上游走,求从一个点走到另一个点的期望步数。 设 E [ i , j ] 表 示 从 i 到 j 的 期 望 步 数 E [ i , j ] = E [ x , y ] = P ( i ! = j 且 x ! = y ) ⇒ P = 1 n − 1 ⇒ A n s = 1 P = n − 1 \begin{aligned} &设E[i,j]表示从i到j的期望步数\\ &E[i,j]=E[x,y]=P(i!=j且x!=y)\\ &\Rightarrow P=\frac 1{n-1}\\ &\Rightarrow Ans=\frac 1 P=n-1\end{aligned} 设E[i,j]表示从i到j的期望步数E[i,j]=E[x,y]=P(i!=j且x!=y)⇒P=n−11⇒Ans=P1=n−13、在一张 2 n 2n 2n 个点的完全二分图上游走,求从一个点走到另一个点的期望步数。
设 A : 从 一 个 点 到 同 侧 点 的 步 数 设 B : 从 一 个 点 到 异 侧 点 的 步 数 B = 1 n ∗ 1 + n − 1 n ∗ ( 1 + A ) A = B + 1 然 后 , 解 一 下 方 程 即 可 。 \begin{aligned} &设A:从一个点到同侧点的步数\\ &设B:从一个点到异侧点的步数\\ &B=\frac 1 n*1+\frac{n-1}n*(1+A)\\ &A=B+1\\ &然后,\\ &解一下方程即可。\end{aligned} 设A:从一个点到同侧点的步数设B:从一个点到异侧点的步数B=n1∗1+nn−1∗(1+A)A=B+1然后,解一下方程即可。4、在一张 n n n 个点的菊花图上游走,求从根走到另一个点的期望步数。
有 三 种 情 况 : 1 、 叶 子 → 叶 子 A 2 、 叶 子 → 中 心 1 3 、 中 心 → 叶 子 B ∴ A = 1 + B B = 1 n − 1 ∗ 1 + n − 1 n − 2 ∗ ( 1 + A ) ∴ B = 2 n − 1 \begin{aligned} &有三种情况:\\ &1、叶子\rightarrow叶子\quad A\\ &2、叶子\rightarrow中心\quad 1\\ &3、中心\rightarrow叶子\quad B\\ &\therefore A=1+B\\ &B=\frac 1{n-1}*1+\frac{n-1}{n-2}*(1+A) \\ &\therefore B=2n-1 \end{aligned} 有三种情况:1、叶子→叶子A2、叶子→中心13、中心→叶子B∴A=1+BB=n−11∗1+n−2n−1∗(1+A)∴B=2n−15、在一棵 n n n 个点的树上游走,求从 x x x 走到 y y y 的期望步数。
以 y 为 根 设 f ( x ) 表 示 从 x 第 一 次 到 它 父 亲 的 期 望 , d [ x ] 表 示 x 的 度 数 。 ∴ f ( x ) = 1 d [ x ] + 1 d [ x ] ∗ ∑ i = 1 d [ x ] , i ! = f a [ x ] ( 1 + f ( s o n [ x ] ) + f ( x ) ) 然 后 … … 请 开 始 你 美 妙 的 D P 表 演 ! \begin{aligned} &以y为根\\ &设f(x)表示从x第一次到它父亲的期望,d[x]表示x的度数。\\ &\therefore f(x)=\frac 1 {d[x]}+\frac 1{d[x]}*\sum_{i=1}^{d[x],i!=fa[x]}(1+f(son[x])+f(x))\\ &然后……\\ &请开始你美妙的\mathfrak{DP}表演! \end{aligned} 以y为根设f(x)表示从x第一次到它父亲的期望,d[x]表示x的度数。∴f(x)=d[x]1+d[x]1∗i=1∑d[x],i!=fa[x](1+f(son[x])+f(x))然后……请开始你美妙的DP表演!6、构造一张 200 200 200 个点的无向图,使得从 S S S 走到 T T T 的随机游走期望步数 ⩾ 1 0 6 \geqslant 10^6 ⩾106。
假 设 让 S 成 为 链 的 一 个 端 点 , T 成 为 链 的 另 一 个 端 点 。 由 T 1 得 知 它 的 期 望 步 数 是 n 2 级 别 的 , 假 如 我 们 使 T 1 中 的 E ( x 1 ) = 1 变 为 n 2 即 可 达 到 目 的 。 因 此 我 们 就 可 以 构 造 左 边 一 个 100 个 点 的 完 全 图 , 其 中 一 个 点 延 伸 出 100 个 点 的 链 , 又 根 据 T 2 的 结 论 可 得 E ( x 1 ) = 1 n ∗ 1 + n − 1 n ∗ ( 1 + ( n − 1 ) + E ( x 1 ) ) \begin{aligned} &假设让S成为链的一个端点,T成为链的另一个端点。\\ &由T_1得知它的期望步数是n^2级别的,假如我们使T_1中的E(x_1)=1变为n^2即可达到目的。\\ &因此我们就可以构造左边一个100个点的完全图,其中一个点延伸出100个点的链,\\ &又根据T_2的结论可得\\ &E(x_1)=\frac 1 n*1+\frac{n-1}n*(1+(n-1)+E(x_1)) \end{aligned} 假设让S成为链的一个端点,T成为链的另一个端点。由T1得知它的期望步数是n2级别的,假如我们使T1中的E(x1)=1变为n2即可达到目的。因此我们就可以构造左边一个100个点的完全图,其中一个点延伸出100个点的链,又根据T2的结论可得E(x1)=n1∗1+nn−1∗(1+(n−1)+E(x1))
经典问题
1、每次随机一个 [ 1 , n ] [1,n] [1,n] 的整数,问期望几次能凑齐所有数。
设 x i 表 示 当 前 有 i − 1 个 数 , 一 直 选 , 直 到 有 i 个 数 ⇒ S = ∑ i = 1 n x i ⇒ E ( S ) = ∑ i = 1 n E ( x i ) ∵ E ( x i ) = n − i + 1 n ⇒ A n s = n n − i + 1 \begin{aligned} &设x_i表示当前有i-1个数,一直选,直到有i个数\\ &\Rightarrow S=\sum_{i=1}^n x_i\\ &\Rightarrow E(S)=\sum_{i=1}^nE(x_i)\\ &\because E(x_i)=\frac{n-i+1}n\\ &\Rightarrow Ans=\frac {n}{n-i+1} \end{aligned} 设xi表示当前有i−1个数,一直选,直到有i个数⇒S=i=1∑nxi⇒E(S)=i=1∑nE(xi)∵E(xi)=nn−i+1⇒Ans=n−i+1n2、随机一个长度为 n n n 的排列 p p p ,求 p [ 1 ∼ i ] p[1\sim i] p[1∼i] 中 p [ i ] p[i] p[i] 是最大的数的概率。
我 们 从 整 体 上 看 , 每 个 数 平 等 ∴ A n s = 1 i \begin{aligned} &我们从整体上看,每个数平等\\ &\therefore Ans=\frac 1 i \end{aligned} 我们从整体上看,每个数平等∴Ans=i13、问满足上面那个题的 i i i 的个数的平方的期望。
我 们 设 x i 为 当 前 p [ i ] 是 否 合 法 , 若 合 法 则 为 1 , 否 则 为 0 , x 表 示 满 足 题 意 的 p [ i ] 个 数 , 则 答 案 为 E ( x 2 ) , x = ∑ i x i 。 E ( x 2 ) = E ( ( ∑ i x i ) 2 ) 由 于 期 望 的 线 性 性 , 我 们 把 内 部 分 成 两 个 部 分 , 即 E ( x i ∗ x j ) 和 E ( x i ∗ x i ) 那 么 E ( x 2 ) = E ( ∑ i n ∑ j n , i ! = j x i ∗ x j + ∑ i n x i 2 ) 因 为 x i 不 合 法 的 话 整 个 直 接 为 0 , 所 以 x i 2 可 以 直 接 化 简 为 x i 且 E ( x i ) = 1 i 所 以 原 式 = ∑ i n ∑ j n , i ! = j E ( x i ∗ x j ) + ∑ i n E ( x i ) 又 ∵ 当 i ! = j 时 , p [ i ] , p [ j ] 成 为 各 自 区 间 最 大 值 的 概 率 不 会 相 互 影 响 , 也 就 是 说 , 这 两 个 概 率 相 互 平 等 。 ⇒ E ( x i ∗ x j ) = 1 i j ⇒ A n s = E ( x 2 ) = ∑ i n ∑ j n , i ! = j 1 i j + ∑ i n 1 i \begin{aligned} &我们设x_i为当前p[i]是否合法,若合法则为1,否则为0,\\ &x表示满足题意的p[i]个数,则答案为E(x^2),x=\sum_i x_i。\\ &E(x^2)=E((\sum_i x_i)^2)\\ &由于期望的线性性,我们把内部分成两个部分,即E(x_i*x_j)和E(x_i*x_i)\\ &那么E(x^2)=E(\sum_i^n\sum_j^{n,i!=j}x_i*x_j+\sum_i^nx_i^2)\\ &因为x_i不合法的话整个直接为0,所以x_i^2可以直接化简为x_i且E(x_i)=\frac 1 i\\ &所以原式=\sum_i^n\sum_j^{n,i!=j}E(x_i*x_j)+\sum_i^n E(x_i)\\ &又\because 当i!=j时,p[i],p[j]成为各自区间最大值的概率不会相互影响,\\&也就是说,这两个概率相互平等。\\ &\Rightarrow E(x_i*x_j)=\frac 1 {ij}\\ &\Rightarrow Ans=E(x^2)=\sum_i^n\sum_j^{n,i!=j} \frac 1{ij}+\sum_i^n\frac 1 i\end{aligned} 我们设xi为当前p[i]是否合法,若合法则为1,否则为0,x表示满足题意的p[i]个数,则答案为E(x2),x=i∑xi。E(x2)=E((i∑xi)2)由于期望的线性性,我们把内部分成两个部分,即E(xi∗xj)和E(xi∗xi)那么E(x2)=E(i∑nj∑n,i!=jxi∗xj+i∑nxi2)因为xi不合法的话整个直接为0,所以xi2可以直接化简为xi且E(xi)=i1所以原式=i∑nj∑n,i!=jE(xi∗xj)+i∑nE(xi)又∵当i!=j时,p[i],p[j]成为各自区间最大值的概率不会相互影响,也就是说,这两个概率相互平等。⇒E(xi∗xj)=ij1⇒Ans=E(x2)=i∑nj∑n,i!=jij1+i∑ni14、随机一个长度为 n n n 的排列 p p p ,求 i i i 在 j j j 的后面的概率。
A n s = 1 2 Ans=\frac 1 2 Ans=215、随机一个长度为 n n n 的排列 p p p ,求它包含 w [ 1 ∼ m ] w[1\sim m] w[1∼m] 作为子序列/连续子序列的概率。
F o r m e r : Former: Former:
( n − m ) ! n ! ∗ C n m = 1 m ! \frac{(n-m)!}{n!}*C_n^m=\frac 1{m!} n!(n−m)!∗Cnm=m!1 L a t t e r : Latter: Latter:
取 m 个 位 置 , 那 么 , 第 一 个 位 置 n 种 , 第 二 个 位 置 n − 1 种 , 乘 到 n − m + 1 种 。 则 正 确 的 概 率 为 ∏ i = n − m + 1 n 1 i = ( n − m ) ! n ! 然 后 枚 举 开 头 , 显 然 , 有 n − m + 1 个 位 置 \begin{aligned} &取m个位置,那么,第一个位置n种,第二个位置n-1种,乘到n-m+1种。\\ &则正确的概率为\prod_{i=n-m+1}^n\frac 1 i=\frac{(n-m)!}{n!}\\ &然后枚举开头,显然,有n-m+1个位置\\ \end{aligned} 取m个位置,那么,第一个位置n种,第二个位置n−1种,乘到n−m+1种。则正确的概率为i=n−m+1∏ni1=n!(n−m)!然后枚举开头,显然,有n−m+1个位置 ( n − m + 1 ) ! n ! \frac{(n-m+1)!}{n!} n!(n−m+1)!总结:其实很多概率期望问题都可以转化为计数问题,有时候不能太死,试试计数吧!
6、有 n n n 堆石头,第 i i i 堆个数为 a [ i ] a[i] a[i] ,每次随机选一个石头然后把那一整堆都扔了,求第 1 1 1 堆石头期望第几次被扔。
设 A [ i ] 表 示 第 i 堆 石 头 是 第 几 个 被 拿 走 的 A [ 1 ] = ∑ i c h e c k ( A [ i ] ⩽ A [ 1 ] ) ∗ c h e c k ( ) 表 示 括 号 内 的 真 假 , 为 真 则 返 回 1 , 否 则 为 0 根 据 期 望 的 线 性 性 ( 太 强 了 ! ) ⇒ E ( A [ 1 ] ) = ∑ i E ( A [ i ] ⩽ A [ 1 ] ) = 1 + ∑ i = 2 P ( A [ i ] < A [ 1 ] ) P ( A [ i ] < A [ 1 ] ) = a [ i ] a [ 1 ] + a [ i ] E ( A [ 1 ] ) = 1 + ∑ i = 2 a [ i ] a [ 1 ] + a [ i ] \begin{aligned} &设A[i]表示第i堆石头是第几个被拿走的\\ &A[1]=\sum_{i} check(A[i]\leqslant A[1])\\ &*check()表示括号内的真假,为真则返回1,否则为0\\ &根据期望的线性性(太强了!)\\ &\Rightarrow E(A[1])=\sum_i E(A[i]\leqslant A[1])\\ &\qquad\qquad\quad=1+\sum_{i=2}P(A[i]<A[1])\\ &P(A[i]<A[1])=\frac{a[i]}{a[1]+a[i]}\\ &E(A[1])=1+\sum_{i=2}\frac{a[i]}{a[1]+a[i]} \end{aligned} 设A[i]表示第i堆石头是第几个被拿走的A[1]=i∑check(A[i]⩽A[1])∗check()表示括号内的真假,为真则返回1,否则为0根据期望的线性性(太强了!)⇒E(A[1])=i∑E(A[i]⩽A[1])=1+i=2∑P(A[i]<A[1])P(A[i]<A[1])=a[1]+a[i]a[i]E(A[1])=1+i=2∑a[1]+a[i]a[i]
总结:对于期望题,我们先定义答案,然后根据期望的线性性写出目标状态期望,再利用公式拆分,然后用你强大的智商将其化简即可。