深度优先搜索
深度优先,顾名思义,只要有路,则一条路走到底,然后回溯,看之前的叉路口是否还有路可选。
一、基本概念
深度优先搜索 是一种图的遍历算法,可用于求单源最短路径。
算法思路

看图说话!如上是一个有向图。
假设我们需要找到从1到4结点的路径。那么从结点1开始遍历,然后递归的遍历所有与1相邻的结点。所以,第一,我们需要构建图的邻接矩阵(建模很重要),并初始化。
为了避免遍历完1结点后,在跳到2结点时,又往回遍历1结点。所以,第二,我们需要用一个数组visited来标记 已遍历过 的结点(简单的hash表)。
前面讲过,深度优先其实就是先一条路走到黑。那么,在从1到2后,就应该是在2的邻接结点中选择一个结点(此前已将1和2结点标记为了已遍历),假如选择3,那么接下来就是从3的邻接结点中选择一个结点,如上只能选择4(visited[1] != 0),因此1-2-3-4便是1到4的一条路径。
如此,便完成了一次深度搜索。 如果任务重新修改为找到从1到4节点的最短路径,虽然通过上述过程,我们已经找到了一条路径。但是此时,并不能确定此为最短。因为,在之前的叉路口,还有其他路径可选时,比如在节点2的时候,除了3这个选择,我们还可以选择5,因此,我们还需要重新回到2节点,然后看看如果接下来我们选择5,会不会有可能也可以到达4,并且路程缩短。 基于这个想法,进入下一个步骤。
首先是在4结点的基础上回溯到3结点,由于3只有一个往外地指向,所以继续回溯到2结点。(注意,回溯的时候需要将此前标记过的结点去除标记,即将4和3去除标记)。在回溯到2结点时,发现还有一条可走的路径,即跳转到5,然后接下来的过程便是重复上述步骤。最后发现新的路径: 1-2-5-3-4 。在此,基于结点2的所有可能路径便已全部遍历完。于是再从2回溯到1(并将2标记为未遍历),将1其余的邻接结点按照上述步骤重复。
二、举例说明
1. 求最短路径
假设有5个城市,城市之间的道路情况如下图所示,1和2之间的单向箭头表示只能从1到2,箭头上面的数字表示城市之间的距离。要求计算从1到5之间的最短距离。
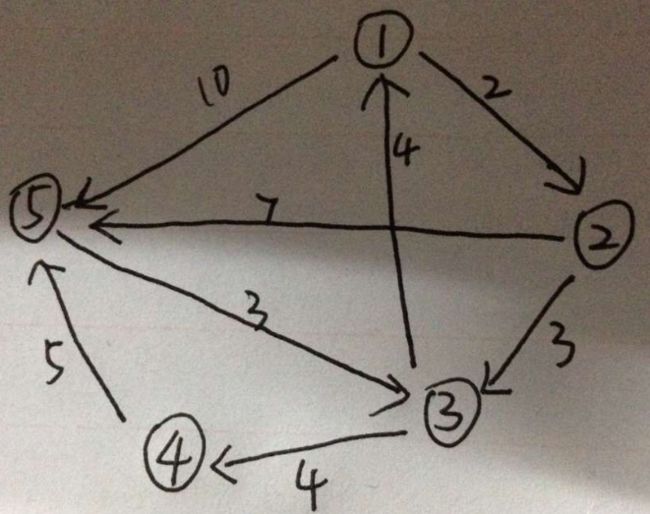
构建邻接矩阵:
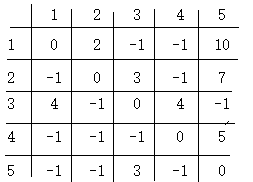
初始一个数组用于记录每个节点是否被遍历。
visited[]在当前结点处,判断与其他结点是否有通路(-1表示没有)。例如,假设当前在结点1,判断与其他结点之间的关系,只需要遍历一个一维数组就可以了(第一行)。
发现 [1,2] 位置 > 0 时,则表示1和2之间有通路,如果
visited[2] = 0则表示节点2没有被访问过,那么也就代表着此时站在节点1时,可以从节点1过渡到节点2, 然后再执行visited[2] = 1以标识节点2被访问了。通过第4步,到达了节点2。此时,由于节点2不是目的节点,则需要站在节点2的位置,继续“选路”,也就是遍历第二行,从第二行中找到可选节点。剩下的过程就是重复步骤4和步骤5,直到没有路可选了 或者 已到达目的节点。然后就是回溯,也就是从最深一层的递归中退出来时,将之前访问过的节点重新标记为未访问,然后就是再重复之前过程。。。(表述有点不清晰,代码说话= =)
代码如下:
/*
深度优先搜索算法
作者:Zoo
时间:2016年4月16日12:45:19
*/
#include // for cout
#include // for memset
#define N 100
using namespace std;
int city_n ; //城市的数量
int road_n ; //道路的数量
int minDis = -1; //最短路程 -1 表示此数值无效
int visited[N]; //已经路过的城市
int edge[N][N]; //邻接矩阵 : -1 表示此路不通
int city_tar; //目标城市
/*
深度优先搜索算法
cur int 当前结点
dis int 已走过的路程
*/
void dfs(int cur, int dis);
int main()
{
cout << "输入城市数量 和 路的总数【eg :5 8 总共5个城市 8条单向通道】" <cin >> city_n >> road_n;
// 初始化邻接矩阵
memset(*edge,-1,4*N*(city_n+1));
for(int i = 0 ; i <= city_n ; i++)
{
edge[i][i] = 0; // 自己到自己的距离是0
}
cout << "输入城市之间的道路情况【eg : 1 2 8 城市1到2的路程为8】" <int city_s,city_d; //路的起始城市,和 目的城市
int dis; //距离
for(int i = 0; i < road_n; i++)
{
cin >> city_s >> city_d >> dis;
edge[city_s][city_d] = dis;
}
/* 输入出发点 和 目标点 */
int city_cur;
cout << "输入出发点 和 目标点【eg : 1 5 从城市1出发到城市5】" <cin >> city_cur >> city_tar ;
visited[city_cur] = 1;
dfs(city_cur,0);
cout << minDis << endl;
return 0;
}
void dfs(int cur, int dis)
{
//如果当前走过的路程已经大于之前找到的最短路径,则返回
if( minDis >= 0 && dis > minDis )
return;
if( cur == city_tar ) // 如果当前结点为目标结点,则判断是否需要更新最短路程
{
if( (minDis >= 0 && dis < minDis) || ( minDis == -1) )
minDis = dis;
return;
}
// 此处就相当于对一个一维数组的遍历
for( int i = 1 ; i <= city_n; i++)
{
if(edge[cur][i] >= 0 && visited[i] == 0)
{
/* 标记为已走过的结点 */
visited[i] = 1;
dfs(i,dis+edge[cur][i]);
/* 回溯时将结点状态重置 */
visited[i] = 0;
}
}
return;
} 测试数据:
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
1 5结果如下:
2. 求两个节点之间的所有路径
接着上面的题目,此时假设要求任意两个结点之间的路径。
/*
深度优先搜索算法
作者:Zoo
时间:2016年4月16日12:45:19
*/
#include // for cout
#include // for memset
#include 测试数据改为求1和4结点之间的所有路径。
结果如下:
3. 迷宫
以下是一个迷宫的示意图,标有1的空格表示为障碍物,求从起始位置到目的位置的最短步数。注意:每次只能在当前位置的上下左右四个方向移动一格,要求只能在迷宫内移动,并且遇到障碍物只能绕道而行。(此题是针对 广度优先搜索 中问题的深度优先写法。)
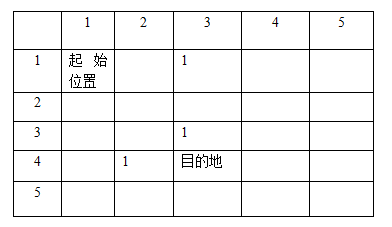
代码如下:
#include cin >> row >> col;
cout << "input the map's info " <for(int i = 1; i <= row ; i++)
{
for(int j = 1; j <= col ; j++)
{
cin >> map[i][j];
}
}
cout << "input start pos and target pos" <int sx,sy;
cin >> sx >> sy >> tarx >> tary ;
maze(sx,sy,0);
cout << minDist << endl;
return 0;
} 测试代码:
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3测试结果:
三、说明
if(x == tarx && y == tary)
{
if(step < minDist)
minDist = step;
return;
}上述这段代码中,return 不加上本来也没有错,但是理论上会增加递归次数。因为进入到这个 if 语句也就代表着这次深度搜索达到了目的,按要求应该是回溯至上一节点,去其他分支看看有没有另外一条路能够使得最短路径减小。而如果不加上return , 那么就会再一次进入到下面的for循环中,那么只要当前结点的上下左右四个方向中,存在任何一个之前没被访问过的结点(book[i][j] == 0), 那么就会再一次进入递归,而显然这是无意义的。