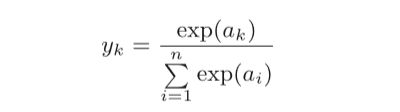深度学习入门笔记（三）

手写数字识别

此后需要用到的代码，均可通过此链接进行下载解压

链接：https://pan.baidu.com/s1FBya4cVub3LgJTJo8yMzMg
提取码：ntca

一. 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况来改变输出层的激活函数。一般来说，分类问题用softmax函数，回归问题用恒等函数。

1. 恒等函数和softmax函数

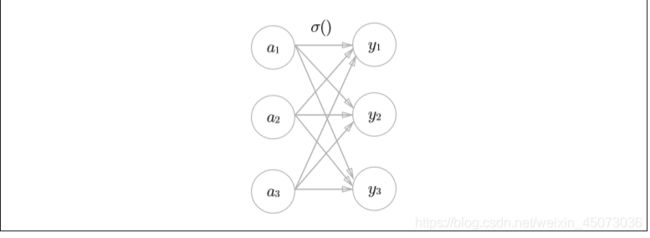
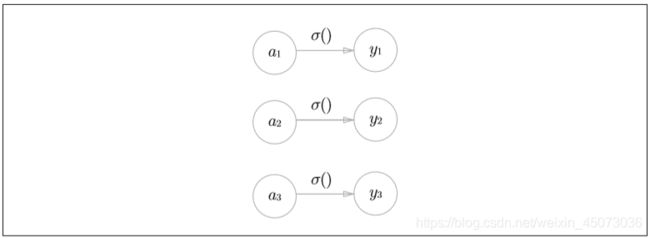
恒等函数会将输入按原样输出，对于输入的信息，不加任何改动地直接输出。因此，在输出层使用恒等函数时，输入信号会原封不动的被输出。另外，将恒等函数的处理过程用之前的神网络图来表示的话。如下图，恒等函数进行的转换处理可以用一根箭头来表示。

恒等函数

而分类问题使用softmax函数:

exp(x)是表示e的x次方的指数函数（e是纳皮尔常数2.7182…）。假设输出层共有n个神经元，计算第k个神经元的输出yk。softmax函数的分子是输入信号ak的指数函数，分母是所有输入信号的指数函数的和。

下面来实现softmax函数:

def softmax(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a

return y

当然需要提前导入numpy，即import numpy as np。

2.实现softmax函数时的注意事项

上面的softmax函数的实现虽然正确描述了式（3.10），但在计算机的运算 上有一定的缺陷。这个缺陷就是溢出问题。softmax函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。比如，e10的值 会超过20000，e100会变成一个后面有40多个0的超大值，e1000的结果会返回 一个表示无穷大的inf。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况。
softmax函数的实现可以用下方公式来进行改进。

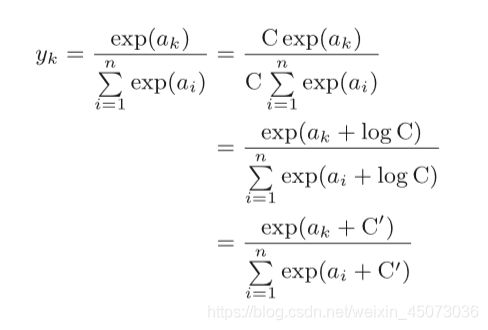
上方式子说明，在进行softmax的指数函数的运算时，加上（或减去）某个常数并不会改变运算的结果。这里的C’可以使用任何值，但是为了防止溢出，我们通过减去输入信号的最大值。

def softmax(x):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

3.softmax函数的特征

softmax()函数，可以在交互环境中按照如下方式计算神经网络的输出

>>> a = np.array([0.3, 2.9, 4.0])
>>> y = softmax(x)
>>> print(y)
[ 0.01821127  0.24519181  0.73659691]
>>> np.sum(y)
1.0

如上所示，softmax函数的输出是0.0到1.0之间的实数。并且，softmax函数的输出值总和是1.输出总和为1是softmax函数的一个重要性质。正因为有了这个性质，我们才可以吧softmax函数的输出解释为“概率”。
这里需要注意的是，即便使用了softmax函数，各个元素之间的大小关系也不会改变。这是因为指数函数是单调递增函数。实际上，上例中的a的个元素的大小关系和y的个元素的大小关系并没有改变。
一般而言，神经网络只能把输出值最大的神经元所对应的类别作为识别果。并且，即便使用softmax函数，输出值最大的神经元的位置也不会变。因此，神经网络在进行分类时，速出层的softmax函数可以省略。在实际问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会省略。

4.输出层的神经元数量

输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量。例如，对于预测0到9数字的问题，此问题明显为分类问题。那么，可以像下图那样，将输出层的神经元个数设定为10。

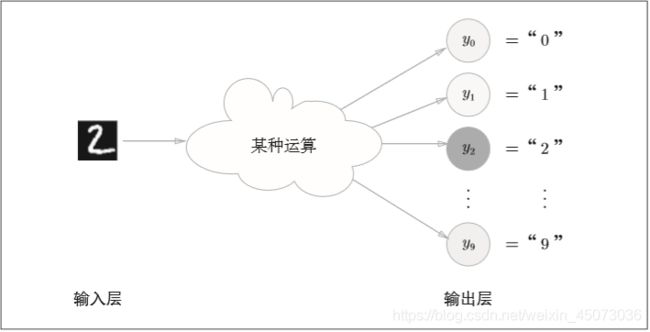
如上图所示，在这个例子中，输出层的神经元从上往下一次对应数字0,1,…,9。此外，图中输出层的神经元的值用不同的灰度来表示。这个例子中y2颜色最深，输出的值最大。表明这个神经网络预测的时y2对应的类别，也就是“2”.

二. 手写数字识别

这里我们假设学习已经完全结束，我们使用学习到的参数(权重和偏置)，先实现神经网络的“推理处理”。这个推理处理也称作神经网络的前向传播(forward propagation)。

1.MNIST数据集

这里我们使用的数据集是MNIST手写数字图像集。MNIST是机器学习领域最有名的数据集之一，被广泛应用到从简单的试验到发表的论文研究等各种场合。
MNIST数据集是从0到9的数字图像构成的。训练图像(训练集)有6万张，测试图像(测试集)有1万张，这些图像可以用于徐熙和推理。

MNIST数据集

MNIST的图像数据是28×28像素的灰度图像(通道数为1)，各个像素的取值都在0到255之间。每个图像数据都相应的标有“1”，“6”，“9”等标签(label)。
《深度学习入门》提供了方便的Python脚本mnist.py，该脚本支持从下载MNIST数据集到将这些数据转换成NumPy数组等处理(mnist.py在dataset目录下)。使用 mnist.py时，当前目录必须是ch01、ch02、ch03、…、ch08目录中的一个。使用mnist.py中的load_mnist()函数，就可以按下述方式轻松读入MNIST数据。

import sys,os
sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定
from dataset.mnist import load_mnist

# 第一次调用会花费几分钟
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

# 输出各个数据的形状
print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000,)
print(x_test.shape)  # (10000, 784)
print(t_test.shape)  # (10000,)

首先，为了导入父目录中的文件，进行相应的设定A。然后，导入 dataset/mnist.py中的load_mnist函数。最后，使用load_mnist函数，读入 MNIST数据集。第一次调用load_mnist函数时，因为要下载MNIST数据集， 所以需要接入网络。第2次及以后的调用只需读入保存在本地的文件（pickle文件）即可，因此处理所需的时间非常短。
load_mnist函数以“(训练图像,训练标签)，(测试图像，测试标签)”的 形式返回读入的MNIST数据。此外，还可以像load_mnist(normalize=True, flatten=True, one_hot_label=False) 这样，设置3个参数。第 1 个参数 normalize设置是否将输入图像正规化为0.0～1.0的值。如果将该参数设置 为False，则输入图像的像素会保持原来的0～255。第2个参数flatten设置 是否展开输入图像（变成一维数组）。如果将该参数设置为False，则输入图像为1×28×28的三维数组；若设置为True，则输入图像会保存为由784个元素构成的一维数组。第3个参数one_hot_label设置是否将标签保存为onehot表示（one-hot representation）。 one-hot表示是仅正确解标签为1，其余皆为0的数组，就像[0,0,1,0,0,0,0,0,0,0]这样。当one_hot_label为False时，只是像7、2这样简单保存正确解标签；当one_hot_label为True时，标签则保存为one-hot表示。
用于读入MNIST数据集的load_mnist()函数内部也使用了pickle功能（在第2次及以后读入时）。利用pickle功能，可以高效地完成MNIST数据的准备工作。
现在，试着显示MNIST图像，同时确认一下数据。图像的像是使用PIL(Python Image Library,若已经有了pillow模块，则不需要单独下载此模块)。执行下述代码之后，训练图像的第一张就会显示出来（源代码在ch03/mnist_show.py中）。

import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

(x_train, t_train), (x_teat, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5

print(img.shape) # (784,)
img = img.reshape(28, 28) # 把图像的形状变成原来的尺寸
print(img.shape) # (28, 28)

img_show(img)

pil_img = Image.fromarray(np.uint8(img)) 这个语句是把保存为numpy数组的图像数据转换为PIL用的数据对象，这个转换处理由Image.fromarray()来完成。

显示MNIST图像

2.神经网络的推理处理

下面，我们对这个MNIST数据集实现神经网络的推理处理。神经网络 的输入层有784个神经元，输出层有10个神经元。输入层的784这个数字来 源于图像大小的28×28 = 784，输出层的10这个数字来源于10类别分类（数 字0到9，共10类别）。此外，这个神经网络有2个隐藏层，第1个隐藏层有 50个神经元，第2个隐藏层有100个神经元。这个50和100可以设置为任何值。下面我们先定义get_data()、init_network()、predict()这3个函数（代码在 ch03/neuralnet_mnist.py中）。

def get_data():
    (x_train, t_train), (x_test, t_test) = \
        load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

init_network()会读入保存在pickle文件sample_weight.pkl中的学习到的权重参数A。这个文件中以字典变量的形式保存了权重和偏置参数。
现在我们用这三个函数来实现神经网络的推理处理。然后，评价此神经网络的识别精度(accuracy)，即能在多大程度上正确分类。

x, t = get_data()
network = init_network()

accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y)
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

首先获得MNIST数据集，生成网络。接着，用for语句逐一取出保存 在x中的图像数据，用predict()函数进行分类。predict()函数以NumPy数 组的形式输出各个标签对应的概率。比如输出[0.1, 0.3, 0.2, …, 0.04]的数组，该数组表示“0”的概率为0.1，“ 1”的概率为0.3，等等。然后，我们 取出这个概率列表中的最大值的索引（第几个元素的概率最高），作为预测结果。可以用np.argmax(x)函数取出数组中的最大值的索引，np.argmax(x)将获取被赋给参数x的数组中的最大值元素的索引。最后，比较神经网络所预测的答案和正确解标签，将回答正确的概率作为识别精度。
执行上面的代码后，会显示“Accuracy:0.9352”。这表示有93.52%的数据被正确分类了。目前我们的目标是运行学习到的神经网络，所以不讨论识别精度本身，不过以后我们会花精力在神经网络的结构和学习方法上，思考如何进一步提高这个精度。实际上，我们打算把精度提高到99%以上。
另外，在这个例子中，我们把load_mnist函数的参数normalize设置成True。将normalize设置成True后，函数内部会进行转换，将图像的各个像素值除以255，使得数据的值在0.0～1.0的范围内。像这样把数据限定到某个范围内的处理称为正规化（normalization）。此外，对神经网络的输入数据 进行某种既定的转换称为预处理（pre-processing）。这里，作为对输入图像的一种预处理，我们进行了正规化。

3.批处理

下面我们使用Python解释器，输出刚才的神经网络的各层的权重的形状。

>>> x, _ = get_data()
>>> network = init_network()
>>> W1, W2, W3 = network['W1'], network['W2'], network['W3']
>>>
>>> x.shape
(10000, 784)
>>> x[0].shape
(784,)
>>> W1.shape
(784, 50)
>>> W2.shape
(50, 100)
>>> W3.shape
(100, 10)

我们通过上述结果确认多维数组的对应维度的元素个数是否是一致的(这里省略了偏置)。

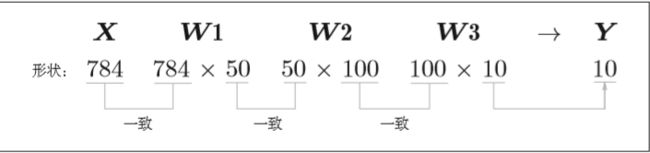
从整体的处理流程来看，图3-26中，输入一个由784个元素（原本是一 个28×28的二维数组）构成的一维数组后，输出一个有10个元素的一维数组。 这是只输入一张图像数据时的处理流程。 现在我们来考虑打包输入多张图像的情形。比如，我们想用predict()函数一次性打包处理100张图像。为此，可以把x的形状改为100×784，将100张图像打包作为输入数据。用图表示的话，如图所示。

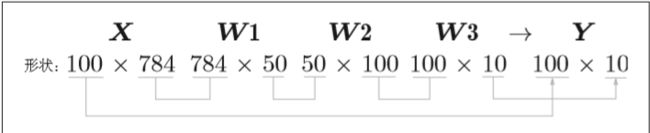
输入数据的形状为100×784，输出数据的形状为100×10.这表示输入的100张图像的结果被一次性输出了。这种打包式的输入数据称为批(batch)。

下面是基于批处理的代码实现：

x, t = get_data()
network = init_network()

batch_size = 100 # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

关于是range()函数。range()函数若指定为range(start, end)，则会生成一个由start到end-1之间的整数构成的 列表。若像range(start, end, step)这样指定3个整数，则生成的列表中的下一个元素会增加step指定的值。
如:

>>> list(range(0, 10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> list(range(0, 10, 3))
[0, 3, 6, 9]

然后，通过argmax()获取值最大的元素的索引。不过这里需要注意的是， 我们给定了参数axis=1。这指定了在100×10的数组中，沿着第1维方向（以第1维为轴）找到值最大的元素的索引（第0维对应第1个维度）。
如:

>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6], ···      [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
>>> y = np.argmax(x, axis=1)
>>> print(y)
[1 2 1 0]

最后，我们比较一下以批为单位进行分类的结果和实际的答案。

如:

>>> y = np.array([1, 2, 1, 0])
>>> t = np.array([1, 2, 0, 0])
>>> print(y==t)
[True True False True]
>>> np.sum(y == t)
3

至此，批处理的代码实现介绍完了。使用批处理，我们可以实现告诉且高效的运算。有利于神经网络的学习训练及推理预测。

• 小结
  • 神经网络中的激活函数使用平滑变化的sigmoid函数后ReLU函数。
  • 通过numpy可以高效实现神经网络。
  • 机器学习的问题可大致分为回归问题和分类问题。
  • 关于输出层的激活函数，回归问题中一般用恒等函数，分类问题中一般用softmax函数。
  • 分类问题中，输出层的神经元的数量设置取决于要分类的类别数。
  • 输入数据的集合称为批(batch)。通过以批为单位进行推理处理，能够实现高速的运算。