【GBDT模型】{0} —— GBDT模型简介及数学推导
什么是 G B D T GBDT GBDT ?
G B D T GBDT GBDT 是机器学习领域中浅层模型的优秀模型,也是各大数据挖掘比赛中经常出现的框架,其全称是 G r a d i e n t B o o s t i n g D e c i s i o n T r e e Gradient Boosting Decision Tree GradientBoostingDecisionTree,中文名是梯度提升树。
B o o s t i n g Boosting Boosting
B o o s t i n g Boosting Boosting 是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值 T T T,最终将这 T T T 个基学习器进行加权结合。
G B D T GBDT GBDT 的损失函数:
B o o s t i n g Boosting Boosting 的模型是个迭代多轮的加法模型。 B o o s t i n g Boosting Boosting 每轮迭代输出的是一个基模型 f m ( x ) f_m(x) fm(x),其中 m m m 表示第 m m m 轮迭代。最终,每轮迭代输出的模型经过加法求和,就得到了最终 B o o s t i n g Boosting Boosting 模型的输出,也就是: y = ∑ m = 1 M f m ( x ) y=\sum^{M}_{m=1}f_m(x) y=m=1∑Mfm(x)
G B D T GBDT GBDT 模型的基模型为 D T DT DT(决策树),即对于 G B D T GBDT GBDT 下的每轮迭代,输出的 f m ( x ) f_m(x) fm(x) 为决策树。而最终的 G B D T GBDT GBDT 模型为所有决策树输出结果之和。 B o o s t i n g Boosting Boosting 的基模型采用的都是弱模型,因此,通常 G B D T GBDT GBDT 基模型的决策树树深不会太深(一般少于 5 5 5 层),这些可以在实际实现中灵活处理。
回归决策树的 损失函数 采用平方误差, G B D T GBDT GBDT 也可以保持一致。平方误差的公式为: L ( w ) = ∑ i = 1 n ( y ^ i − y i ) 2 (1) L(w)=\sum^n_{i=1}(\hat{y}_i-y_i)^2\tag{1} L(w)=i=1∑n(y^i−yi)2(1)
此处的模型和损失函数都是参数 w w w 的函数,参数 w w w 为每个基模型的每个分裂特征和每个分裂阈值。
考虑此时要最优化的目标变量是什么,此处可以从损失函数入手,对于损失函数中的预测值 y i y_i yi 有: y i = ∑ m = 1 M f m ( x i ) = ∑ m = 1 M − 1 f m ( x i ) + f M ( x i ) (2) y_i=\sum_{m=1}^Mf_m(x_i)=\sum^{M-1}_{m=1}f_m(x_i)+f_M(x_i)\tag{2} yi=m=1∑Mfm(xi)=m=1∑M−1fm(xi)+fM(xi)(2)
将 ( 2 ) (2) (2) 式代入 ( 1 ) (1) (1) 式,得: L ( w ) = ∑ i = 1 n ( y ^ i − y i ) 2 = ∑ i = 1 n ( y ^ i − ∑ m = 1 M − 1 f m ( x i ) − f M ( x i ) ) 2 (3) L(w)=\sum^n_{i=1}(\hat{y}_i-y_i)^2=\sum^n_{i=1}(\hat{y}_i-\sum^{M-1}_{m=1}f_m(x_i)-f_M(x_i))^2\tag{3} L(w)=i=1∑n(y^i−yi)2=i=1∑n(y^i−m=1∑M−1fm(xi)−fM(xi))2(3)
观察式 ( 3 ) (3) (3),发现损失函数中有 3 3 3 项。第一项是真实值,第二项是截止到第 M − 1 M-1 M−1 棵树的预测值,第三项是第 M M M 棵树的输出结果,若令: r i = y ^ i − ∑ m = 1 M − 1 f m ( x i ) (4) r_i=\hat{y}_i-\sum^{M-1}_{m=1}f_m(x_i)\tag{4} ri=y^i−m=1∑M−1fm(xi)(4)
表示的是,在训练第 M M M 棵树时,截止到当前的残差值(误差),把 ( 4 ) (4) (4) 代入 ( 3 ) (3) (3),有: L ( w ) = ∑ i = 1 n ( r i − f M ( x i ) ) 2 (5) L(w)=\sum^n_{i=1}(r_i-f_M(x_i))^2\tag{5} L(w)=i=1∑n(ri−fM(xi))2(5)
该公式表明,为了让损失函数数值最小,在训练某个基模型时,其训练目标是去拟合残差 r i r_i ri。
G B D T GBDT GBDT 的最优化求解
上述讨论是基于损失函数为平方误差的情况。一般地,如果损失函数不是平方误差,则每个基模型的训练目标就不是残差。 G B D T GBDT GBDT 利用损失函数的负梯度在当前模型的值作为残差的近似值,即: r i ≈ − [ ∂ L ( w ) ∂ f M − 1 ( x ) ] (6) r_i≈-\bigg[\frac{∂L(w)}{∂f_{M-1}(x)}\bigg]\tag{6} ri≈−[∂fM−1(x)∂L(w)](6)
特别地,当损失函数采用平方误差时,损失函数的负梯度就是先前推导的残差: − [ ∂ L ( w ) ∂ f M − 1 ( x ) ] = y ^ i − ∑ m = 1 M − 1 f m ( x i ) (7) -\bigg[\frac{∂L(w)}{∂f_{M-1}(x)}\bigg]=\hat{y}_i-\sum^{M-1}_{m=1}f_m(x_i)\tag{7} −[∂fM−1(x)∂L(w)]=y^i−m=1∑M−1fm(xi)(7)
假设有一个回归问题,特征只有一个维度,取值范围为 1 1 1 ~ 5 5 5 的自然数,样本对应的真实值取值为 − 1 -1 −1 ~ 1 1 1 的自然数。现利用 G B D T GBDT GBDT 算法建立模型,假设基模型采用树深为 1 1 1 的 C A R T CART CART 回归树算法,损失函数采用平方误差函数,则残差公式为: r i = − [ ∂ L ( w ) ∂ f M − 1 ( x ) ] = y ^ i − ∑ m = 1 M − 1 f m ( x i ) (8) r_i=-\bigg[\frac{∂L(w)}{∂f_{M-1}(x)}\bigg]=\hat{y}_i-\sum^{M-1}_{m=1}f_m(x_i)\tag{8} ri=−[∂fM−1(x)∂L(w)]=y^i−m=1∑M−1fm(xi)(8)
建模通过多轮迭代,每一轮都学习一棵 C A R T CART CART 树,学习的目标是残差。对于只有 1 1 1 层结点的 C A R T CART CART 树建模,采用选择平方误差最小的分裂点和阈值即可。第一轮输出结果为:
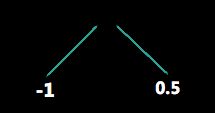
经过第一轮的模型,对每个样本计算出残差表如下:
| 样本序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 特征 x | 1 | 2 | 3 | 4 | 5 |
| 真实值 y | -1 | 1 | 1 | -1 | 1 |
| 预测值 y i ^ \hat{y_i} yi^ | -1 | 0.5 | 0.5 | 0.5 | 0.5 |
| 残差值 r i r_i ri | 0 | 0.5 | 0.5 | -1.5 | 0.5 |
第二轮建模以残差值 r i r_i ri 为标签,构建模型 r i = f ( x ) r_i=f(x) ri=f(x) 的一层 C A R T CART CART 回归树,则有:
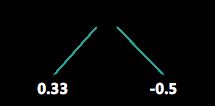
第二轮建模之后的模型如下。同样可以计算残差,并进行第三轮的建模:

重复上述过程 5 5 5 次后,得到模型。
以 x = 2 x=2 x=2 为例代入模型,则每个树的输出结果分别为: 0.5 0.5 0.5、 0.33 0.33 0.33、 − 0.25 -0.25 −0.25、 0.25 0.25 0.25、 − 0.09 -0.09 −0.09,最终预测结果为 y = 0.74 y=0.74 y=0.74 。
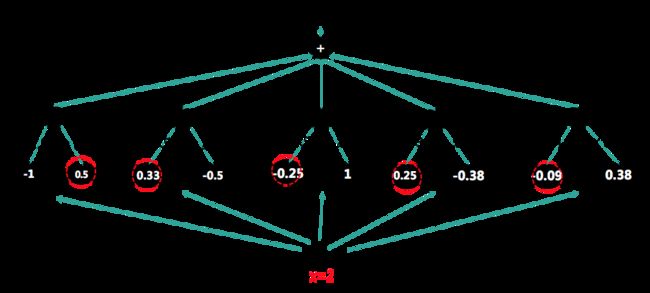
对于 G B D T GBDT GBDT 而言,弱模型可以采用浅层的 C A R T CART CART 树,而提升方法则是一个逐步迭代的加法模型,对于每轮的迭代,采用损失函数的负梯度作为学习目标: r i ≈ − [ ∂ L ( w ) ∂ f M − 1 ( x ) ] (9) r_i≈-\bigg[\frac{∂L(w)}{∂f_{M-1}(x)}\bigg]\tag{9} ri≈−[∂fM−1(x)∂L(w)](9)
至此,得到 G B D T GBDT GBDT 模型。
Reference:https://kaiwu.lagou.com/course/courseInfo.htm?courseId=15#/detail/pc?id=225