【机器学习基础】数学推导+纯Python实现机器学习算法14：Ridge岭回归

Python机器学习算法实现

Author：louwill

     

     上一节我们讲到预防过拟合方法的Lasso回归模型，也就是基于L1正则化的线性回归。本讲我们继续来看基于L2正则化的线性回归模型。

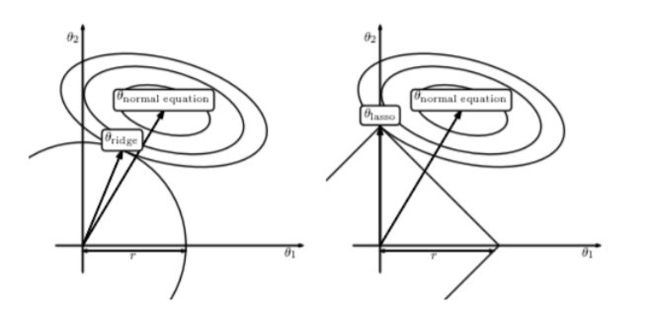
L2正则化

     相较于L0和L1，其实L2才是正则化中的天选之子。在各种防止过拟合和正则化处理过程中，L2正则化可谓第一候选。L2范数是指矩阵中各元素的平方和后的求根结果。采用L2范数进行正则化的原理在于最小化参数矩阵的每个元素，使其无限接近于0但又不像L1那样等于0，也许你又会问了，为什么参数矩阵中每个元素变得很小就能防止过拟合？这里我们就拿深度神经网络来举例说明吧。在L2正则化中，如何正则化系数变得比较大，参数矩阵W中的每个元素都在变小，线性计算的和Z也会变小，激活函数在此时相对呈线性状态，这样就大大简化了深度神经网络的复杂性，因而可以防止过拟合。

     加入L2正则化的线性回归损失函数如下所示。其中第一项为MSE损失，第二项就是L2正则化项。

      L2正则化相比于L1正则化在计算梯度时更加简单。直接对损失函数关于w求导即可。这种基于L2正则化的回归模型便是著名的岭回归(Ridge Regression)。

Ridge

     有了上一讲的代码框架，我们直接在原基础上对损失函数和梯度计算公式进行修改即可。下面来看具体代码。

导入相关模块：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

读入示例数据并划分：

data = pd.read_csv('./abalone.csv')
data['Sex'] = data['Sex'].map({'M':0, 'F':1, 'I':2})
X = data.drop(['Rings'], axis=1)
y = data[['Rings']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train, X_test, y_train, y_test = X_train.values, X_test.values, y_train.values, y_test.values
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

模型参数初始化：

# 定义参数初始化函数
def initialize(dims):
    w = np.zeros((dims, 1))
    b = 0
    return w, b

定义L2损失函数和梯度计算：

# 定义ridge损失函数
def l2_loss(X, y, w, b, alpha):
    num_train = X.shape[0]
    num_feature = X.shape[1]
    y_hat = np.dot(X, w) + b
    loss = np.sum((y_hat-y)**2)/num_train + alpha*(np.sum(np.square(w)))
    dw = np.dot(X.T, (y_hat-y)) /num_train + 2*alpha*w
    db = np.sum((y_hat-y)) /num_train
    return y_hat, loss, dw, db

定义Ridge训练过程：

# 定义训练过程
def ridge_train(X, y, learning_rate=0.001, epochs=5000):
    loss_list = []
    w, b = initialize(X.shape[1])
    for i in range(1, epochs):
        y_hat, loss, dw, db = l2_loss(X, y, w, b, 0.1)
        w += -learning_rate * dw
        b += -learning_rate * db
        loss_list.append(loss)
        
        if i % 100 == 0:
            print('epoch %d loss %f' % (i, loss))
        params = {
            'w': w,
            'b': b
        }
        grads = {
            'dw': dw,
            'db': db
        }
    return loss, loss_list, params, grads

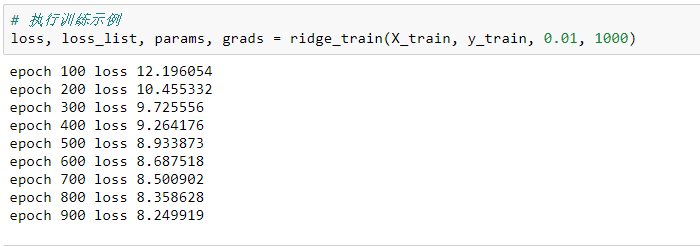
执行示例训练：

# 执行训练示例
loss, loss_list, params, grads = ridge_train(X_train, y_train, 0.01, 1000)

模型参数：

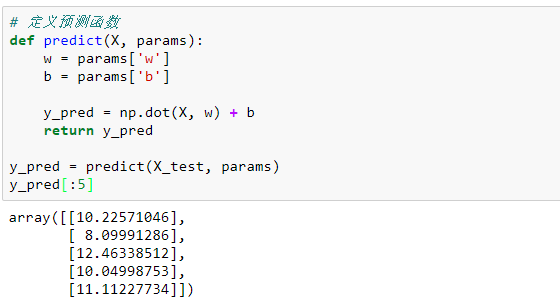
定义模型预测函数：

# 定义预测函数
def predict(X, params):
    w = params['w']
    b = params['b']
    
    y_pred = np.dot(X, w) + b
    return y_pred


y_pred = predict(X_test, params)
y_pred[:5]

测试集数据和模型预测数据的绘图展示：

# 简单绘图
import matplotlib.pyplot as plt
f = X_test.dot(params['w']) + params['b']


plt.scatter(range(X_test.shape[0]), y_test)
plt.plot(f, color = 'darkorange')
plt.xlabel('X')
plt.ylabel('y')
plt.show();

     可以看到模型预测对于高低值的拟合较差，但能拟合大多数值。这样的模型相对具备较强的泛化能力，不会产生严重的过拟合问题。

最后进行简单的封装：

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split


class Ridge():
    def __init__(self):
        pass
        
    def prepare_data(self):
        data = pd.read_csv('./abalone.csv')
        data['Sex'] = data['Sex'].map({'M': 0, 'F': 1, 'I': 2})
        X = data.drop(['Rings'], axis=1)
        y = data[['Rings']]
        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
        X_train, X_test, y_train, y_test = X_train.values, X_test.values, y_train.values, y_test.values
        return X_train, y_train, X_test, y_test
    
    def initialize(self, dims):
        w = np.zeros((dims, 1))
        b = 0
        return w, b


    def l2_loss(self, X, y, w, b, alpha):
        num_train = X.shape[0]
        num_feature = X.shape[1]
        y_hat = np.dot(X, w) + b
        loss = np.sum((y_hat - y) ** 2) / num_train + alpha * (np.sum(np.square(w)))
        dw = np.dot(X.T, (y_hat - y)) / num_train + 2 * alpha * w
        db = np.sum((y_hat - y)) / num_train
        return y_hat, loss, dw, db


    def ridge_train(self, X, y, learning_rate=0.01, epochs=1000):
        loss_list = []
        w, b = self.initialize(X.shape[1])
        for i in range(1, epochs):
            y_hat, loss, dw, db = self.l2_loss(X, y, w, b, 0.1)
            w += -learning_rate * dw
            b += -learning_rate * db
            loss_list.append(loss)
        
            if i % 100 == 0:
                print('epoch %d loss %f' % (i, loss))
            params = {
                'w': w,
                'b': b
            }
            grads = {
                'dw': dw,
                'db': db
            }
        return loss, loss_list, params, grads
    
    
    def predict(self, X, params):
        w = params['w']
        b = params['b']
        y_pred = np.dot(X, w) + b
        return y_pred
    
 
if __name__ == '__main__':
    ridge = Ridge()
    X_train, y_train, X_test, y_test = ridge.prepare_data()
    loss, loss_list, params, grads = ridge.ridge_train(X_train, y_train, 0.01, 1000)
    print(params)

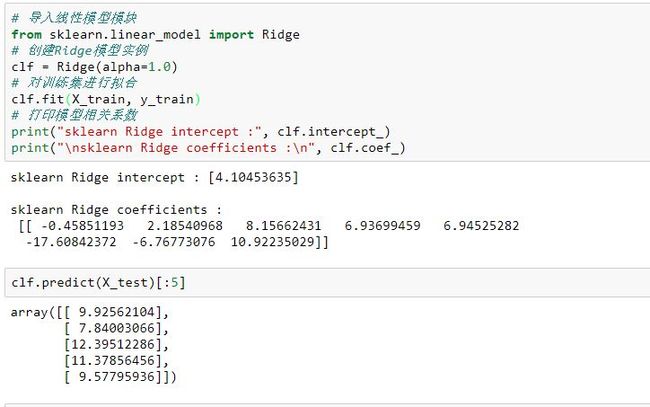
sklearn中也提供了Ridge的实现方式：

# 导入线性模型模块
from sklearn.linear_model import Ridge
# 创建Ridge模型实例
clf = Ridge(alpha=1.0)
# 对训练集进行拟合
clf.fit(X_train, y_train)
# 打印模型相关系数
print("sklearn Ridge intercept :", clf.intercept_)
print("\nsklearn Ridge coefficients :\n", clf.coef_)

     以上就是本节内容，下一节我们将延伸树模型，重点关注集成学习和GBDT系列。

更多内容可参考笔者GitHub地址：

https://github.com/luwill/machine-learning-code-writing

代码整体较为粗糙，还望各位不吝赐教。

参考资料：

Ridge Regression: Biased Estimation for Nonorthogonal Problems

往期精彩：

数学推导+纯Python实现机器学习算法13：Lasso回归

数学推导+纯Python实现机器学习算法12：贝叶斯网络

数学推导+纯Python实现机器学习算法11：朴素贝叶斯

数学推导+纯Python实现机器学习算法10：线性不可分支持向量机

数学推导+纯Python实现机器学习算法8-9：线性可分支持向量机和线性支持向量机

数学推导+纯Python实现机器学习算法7：神经网络

数学推导+纯Python实现机器学习算法6：感知机

数学推导+纯Python实现机器学习算法5：决策树之CART算法

数学推导+纯Python实现机器学习算法4：决策树之ID3算法

数学推导+纯Python实现机器学习算法3：k近邻

数学推导+纯Python实现机器学习算法2：逻辑回归

数学推导+纯Python实现机器学习算法1：线性回归

往期精彩回顾




适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑获取一折本站知识星球优惠券，复制链接直接打开：https://t.zsxq.com/yFQV7am本站qq群1003271085。加入微信群请扫码进群：