力扣刷题系列——数学问题篇
常见的数学相关算法题
以下算法题均为力扣原题,对日常刷题过程中遇到的相关算法题作一个归纳,以便日后复习之用。
1.x的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
代码实现:
class Solution {
public int mySqrt(int x) {
int left=0,right=x,ans=-1;
if(x==0 || x==1){
return x;
}
//二分查找
while(left<=right){
int mid = left+(right-left)/2;
if((long)mid*mid<=x){
left = mid+1;
ans = mid;
}else{
right = mid-1;
}
}
return ans;
}
}2.整数拆分
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
方法一:动态规划
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
for (int i = 2; i <= n; i++) {
int curMax = 0;
for (int j = 1; j < i; j++) {
curMax = Math.max(curMax, Math.max(j * (i - j), j * dp[i - j]));
}
dp[i] = curMax;
}
return dp[n];
}
}
方法二:数学推导
推论一: 若拆分的数量 a 确定, 则 各拆分数字相等时 ,乘积最大。
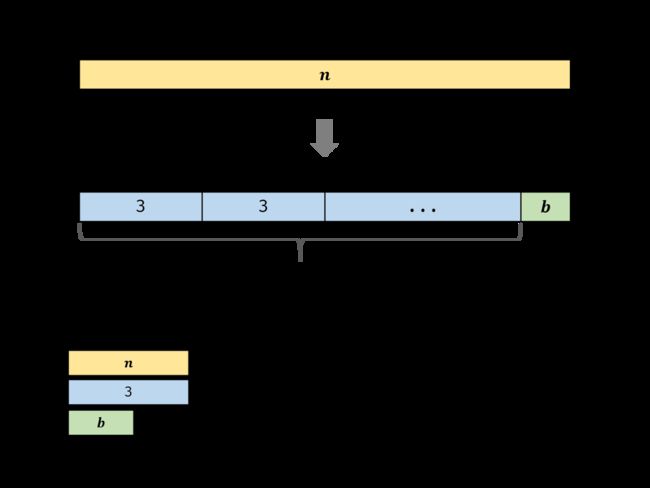
推论二: 将数字 n 尽可能以因子 3 等分时,乘积最大。
算法流程:
class Solution {
public int integerBreak(int n) {
if(n <= 3) return n - 1;
int a = n / 3, b = n % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
3.两个非重叠子数组的最大和
给出非负整数数组 A ,返回两个非重叠(连续)子数组中元素的最大和,子数组的长度分别为 L 和 M。(这里需要澄清的是,长为 L 的子数组可以出现在长为 M 的子数组之前或之后。)
从形式上看,返回最大的 V,而 V = (A[i] + A[i+1] + ... + A[i+L-1]) + (A[j] + A[j+1] + ... + A[j+M-1]) 并满足下列条件之一:
0 <= i < i + L - 1 < j < j + M - 1 < A.length, 或 0 <= j < j + M - 1 < i < i + L - 1 < A.length.
示例 1:
输入:A = [0,6,5,2,2,5,1,9,4], L = 1, M = 2
输出:20
解释:子数组的一种选择中,[9] 长度为 1,[6,5] 长度为 2。
示例 2:
输入:A = [3,8,1,3,2,1,8,9,0], L = 3, M = 2
输出:29
解释:子数组的一种选择中,[3,8,1] 长度为 3,[8,9] 长度为 2。
示例 3:
输入:A = [2,1,5,6,0,9,5,0,3,8], L = 4, M = 3
输出:31
解释:子数组的一种选择中,[5,6,0,9] 长度为 4,[0,3,8] 长度为 3。
代码实现:
class Solution {
public int maxSumTwoNoOverlap(int[] A, int L, int M) {
//两种情况进行比较
int max1 = helper(A,L,M);
int max2 = helper(A,M,L);
return Math.max(max1,max2);
}
public int helper(int[] A,int m,int n){
if(m+n>A.length) return 0;
int i,j;
int max = 0;
int ret1 = 0;
for(i=0;i4.递归乘法
递归乘法。 写一个递归函数,不使用 * 运算符, 实现两个正整数的相乘。可以使用加号、减号、位移,但要吝啬一些。
示例1:
输入:A = 1, B = 10
输出:10
示例2:
输入:A = 3, B = 4
输出:12
代码实现:
class Solution {
public int multiply(int A, int B) {
if(A==0 || B==0)
return 0;
if(A==1)
return B;
if(B==1)
return A;
if(B<0)
return -helper(A,-B);
return helper(A,B);
}
public int helper(int m,int n){
if(n==1){
return m;
}
if(n%2==0){
int half = helper(m,n/2);
return half+half;
}else{
int half = helper(m,n/2);
return half+half+m;
}
}
}5.把字符串转换成整数
写一个函数 StrToInt,实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围,请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) 。
示例 1:
输入: "42"
输出: 42
示例 2:
输入: " -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号,我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3:
输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ,因为它的下一个字符不为数字。
示例 4:
输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号,因此无法执行有效的转换。
示例 5:
输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围,因此返回 INT_MIN (−2^31) 。
代码实现:
class Solution {
public int strToInt(String str) {
char[] c = str.trim().toCharArray();//去除首尾空字符
if(c.length == 0) return 0;
int res = 0, bndry = Integer.MAX_VALUE / 10;//边界
int i = 1, sign = 1;
if(c[0] == '-') sign = -1;
else if(c[0] != '+') i = 0;
for(int j = i; j < c.length; j++) {
if(c[j] < '0' || c[j] > '9') break;
if(res > bndry || res == bndry && c[j] > '7') //学习一下这种判断方法!!!
return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
res = res * 10 + (c[j] - '0');
}
return sign * (int)res;
}
}6.汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
代码实现:
//https://www.cnblogs.com/dmego/p/5965835.html
class Solution {
public void hanota(List A, List B, List C) {
int n=A.size();
move(n,A,B,C);
}
public void move(int n,List A, List B, List C){
if(n==1){
C.add(A.remove(A.size()-1));
return;
}
//递归
move(n-1,A,C,B);
C.add(A.remove(A.size()-1));
move(n-1,B,A,C);
}
}
7.阶乘尾数
设计一个算法,算出 n 阶乘有多少个尾随零。
示例 1:
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。
代码实现:
class Solution {
public int trailingZeroes(int n) {
/*
0 是由 *10 得到的,而 10 是由 2 * 5 得到的
因此我们求 n! 过程中存在多少个 2 * 5
因为 2 的个数必定比 5 的个数多,因此我们只求 5 的个数
如果直接一个一个遍历,即
for(int i = 5; i <= n; i++){
int temp = i;
while(temp % 5 == 0){
count++;
temp /= 5;
}
}
那么 n 过大时,从 1 遍历到 n, 那么会超时,因此我们修改下规律
n! = 1 * 2 * 3 * 4 * (1 * 5) * ... * (2 * 5) * ... * (3 * 5) ...
我们发现,
每隔 5 个数就会出现 一个 5,因此我们只需要通过 n / 5 来计算存在存在多少个 5 个数,那么就对应的存在多少个 5
但是,我们也会发现
每隔 25 个数会出现 一个 25, 而 25 存在 两个 5,我们上面只计算了 25 的一个 5,因此我们需要 n / 25 来计算存在多少个 25,加上它遗漏的 5
同时,我们还会发现
每隔 125 个数会出现一个 125,而 125 存在 三个 5,我们上面只计算了 125 的两个 5,因此我们需要 n / 125 来计算存在多少个 125,加上它遗漏的 5
...
因此我们 count = n / 5 + n / 25 + n / 125 + ...
最终分母可能过大溢出,上面的式子可以进行转换
count = n / 5 + n / 5 / 5 + n / 5 / 5 / 5 + ...
因此,我们这样进行循环
n /= 5;
count += n;
这样,第一次加上的就是 每隔 5 个数的 5 的个数,第二次加上的就是 每隔 25 个数的 5 的个数 ...
*/
int count = 0;
while(n >= 5){
n /= 5;
count += n;
}
return count;
}
}