飞桨PaddlePaddle课程之入门深度学习
飞桨PaddlePaddle课程之入门深度学习
- 1.机器学习和深度学习
- 1.1机器学习
- 机器学习的实现
- 1.2深度学习
- 神经网络的基本概念
- 2.使用Python和Numpy构建神经网络模型
- 2.1波士顿房价预测任务
- 2.2构建神经网络模型
- 数据处理
- 模型设计
- 训练配置
- 训练过程
- 梯度下降法
- 使用Numpy进行梯度计算
- 确定损失函数更小的点
- 3.深度学习平台介绍
- 3.1深度学习框架优势
- 3.2深度学习框架设计思路
- 3.3飞桨开源深度学习平台
- 飞桨开源深度学习平台全景
- 飞桨技术优势
- 飞桨快速安装
- 4.使用飞桨重写房价预测模型
- 4.1使用飞桨构建波士顿房价预测模型
- 数据处理
- 模型设计
- 训练配置
- 训练过程
- 保存并测试模型
- 保存模型
- 测试模型
- 5.学习心得
1.机器学习和深度学习
近些年人工智能、机器学习和深度学习的概念十分火热,在研究深度学习之前,我们先从三个概念的正本清源开始。
概括来说,人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的。人工智能是最宽泛的概念。机器学习是当前比较有效的一种实现人工智能的方式。深度学习是机器学习算法中最热门的一个分支,近些年取得了显著的进展。
1.1机器学习
机器学习的实现
机器学习的实现可以分成两步:训练和预测,类似于我们熟悉的归纳和演绎:
- 归纳: 从具体案例中抽象一般规律,机器学习中的“训练”亦是如此。从一定数量的样本(已知模型输入XXX和模型输出YYY)中,学习输出YYY与输入XXX的关系(可以想象成是某种表达式)。
- 演绎: 从一般规律推导出具体案例的结果,机器学习中的“预测”亦是如此。基于训练得到的YYY与XXX之间的关系,如出现新的输入XXX,计算出输出YYY。通常情况下,如果通过模型计算的输出和真实场景的输出一致,则说明模型是有效的。
1.2深度学习
机器学习算法理论在上个世纪90年代发展成熟,在许多领域都取得了成功应用。但平静的日子只延续到2010年左右,随着大数据的涌现和计算机算力提升,深度学习模型异军突起,极大改变了机器学习的应用格局。今天,多数机器学习任务都可以使用深度学习模型解决,尤其在在语音、计算机视觉和自然语言处理等领域,深度学习模型的效果比传统机器学习算法有显著提升。
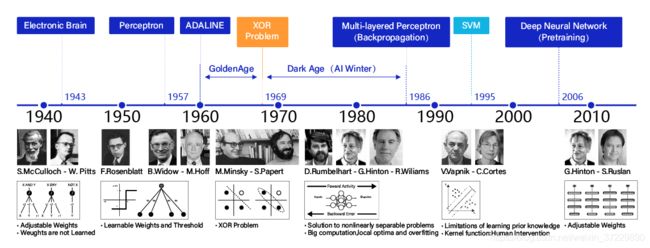
神经网络的基本概念
人工神经网络包括多个神经网络层,如卷积层、全连接层、LSTM等,每一层又包括很多神经元,超过三层的非线性神经网络都可以被称为深度神经网络。通俗的讲,深度学习的模型可以视为是输入到输出的映射函数,足够深的神经网络理论上可以拟合任何复杂的函数。因此神经网络非常适合学习样本数据的内在规律和表示层次,对文字、图像和语音任务有很好的适用性。
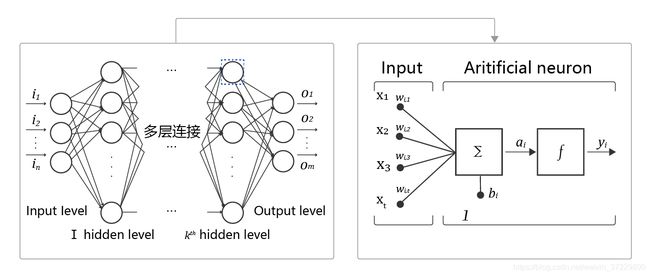
- 神经元: 神经网络中每个节点称为神经元,由两部分组成:
- 加权和:将所有输入加权求和。
- 非线性变换(激活函数):加权和的结果经过一个非线性函数变换,让神经元计算具备非线性的能力。
- 多层连接: 大量这样的节点按照不同的层次排布,形成多层的结构连接起来,即称为神经网络。
- 前向计算: 从输入计算输出的过程,顺序从网络前至后。
- 计算图: 以图形化的方式展现神经网络的计算逻辑又称为计算图。
2.使用Python和Numpy构建神经网络模型
2.1波士顿房价预测任务
波士顿房价预测是一个经典的机器学习任务,类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同,波士顿地区的房价是由诸多因素影响的。该数据集统计了13种可能影响房价的因素和该类型房屋的均价,期望构建一个基于13个因素进行房价预测的模型
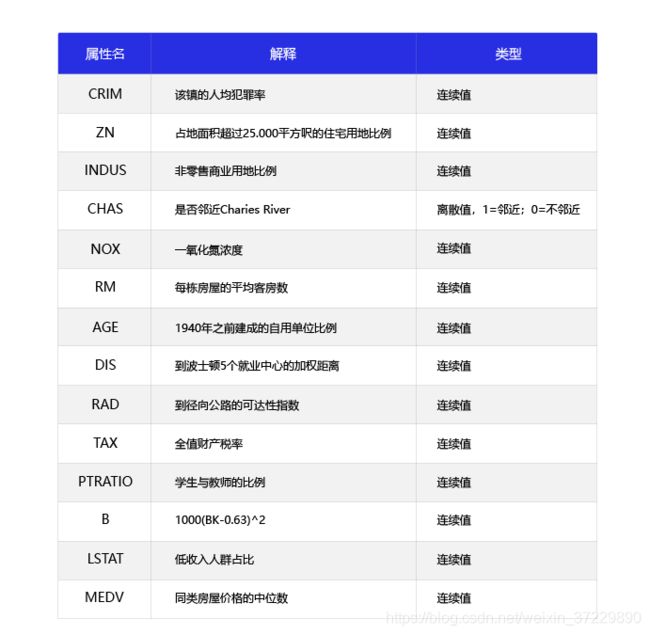
2.2构建神经网络模型
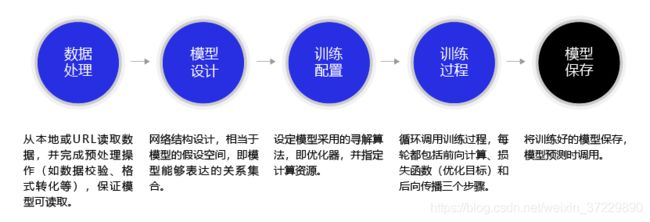
深度学习不仅实现了模型的端到端学习,还推动了人工智能进入工业大生产阶段,产生了标准化、自动化和模块化的通用框架。不同场景的深度学习模型具备一定的通用性,五个步骤即可完成模型的构建和训练。

数据处理
数据处理包含五个部分:数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。数据预处理后,才能被模型调用。
去博客设置页面,选择一款你喜欢的代码片高亮样式,下面展示同样高亮的 代码片.
def load_data():
# 从文件导入数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
# 查看数据
print(x[0])
print(y[0])
[-0.02146321 0.03767327 -0.28552309 -0.08663366 0.01289726 0.04634817
0.00795597 -0.00765794 -0.25172191 -0.11881188 -0.29002528 0.0519112
-0.17590923]
[-0.00390539]
模型设计
模型设计是深度学习模型关键要素之一,也称为网络结构设计,相当于模型的假设空间,即实现模型“前向计算”(从输入到输出)的过程。
如果将输入特征和输出预测值均以向量表示,输入特征x有13个分量,y有1个分量,那么参数权重的形状(shape)是13×1。
将计算预测输出的过程以“类和对象”的方式来描述,类成员变量有参数w和b。通过写一个forward函数(代表“前向计算”)完成上述从特征和参数到输出预测值的计算过程,代码如下所示。
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,
# 此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
net = Network(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)
[-0.63182506]
训练配置
模型设计完成后,需要通过训练配置寻找模型的最优值,即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。
通过模型计算x1表示的影响因素所对应的房价应该是z, 但实际数据告诉我们房价是y。这时我们需要有某种指标来衡量预测值z跟真实值y之间的差距。对于回归问题,最常采用的衡量方法是使用均方误差作为评价模型好坏的指标,具体定义如下:
L o s s = ( y − z ) 2 Loss =(y-z)^{2} Loss=(y−z)2
因为计算损失函数时需要把每个样本的损失函数值都考虑到,所以我们需要对单个样本的损失函数进行求和,并除以样本总数N。
L o s s = 1 N ∑ i = 1 N ( y i − z i ) 2 Loss =\cfrac{1}{N}\displaystyle\sum_{i=1}^N(y_{i}-z_{i})^2 Loss=N1i=1∑N(yi−zi)2
在Network类下面添加损失函数的计算过程如下:
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
net = Network(13)
# 此处可以一次性计算多个样本的预测值和损失函数
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)
predict: [[-0.63182506]
[-0.55793096]
[-1.00062009]]
loss: 0.7229825055441156
训练过程
上述计算过程描述了如何构建神经网络,通过神经网络完成预测值和损失函数的计算。接下来介绍如何求解参数w和b的数值,这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一,其目标是让定义的损失函数Loss尽可能的小,也就是说找到一个参数解w和b使得损失函数取得极小值。
梯度下降法
在现实中存在大量的函数正向求解容易,反向求解较难,被称为单向函数。这种情况特别类似于一位想从山峰走到坡谷的盲人,他看不见坡谷在哪(无法逆向求解出LossLossLoss导数为0时的参数值),但可以伸脚探索身边的坡度(当前点的导数值,也称为梯度)。那么,求解Loss函数最小值可以这样实现:从当前的参数取值,一步步的按照下坡的方向下降,直到走到最低点。这种方法笔者称它为“盲人下坡法”。有个更正式的说法“梯度下降法”。
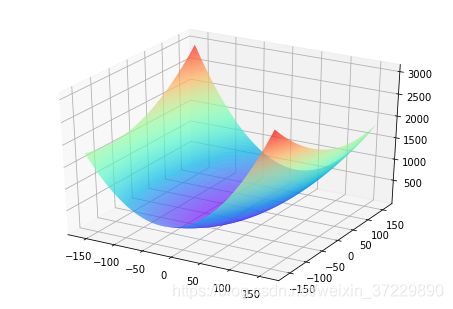
训练的关键是找到一组(w,b),使得损失函数L取极小值。我们先看一下损失函数L只随两个参数w5、w9变化时的简单情形,启发下寻解的思路。
这里我们将w0,w1,…,w12中除w5,w9之外的参数和bbb都固定下来,可以用图画出L(w5,w9)的形式。
net = Network(13)
losses = []
#只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
#计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
#使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.show()
使用Numpy进行梯度计算
上面我们讲过了损失函数的计算方法,这里稍微加以改写。为了梯度计算更加简洁,引入因子1/2,定义损失函数如下:
L o s s = 1 2 N ∑ i = 1 N ( y i − z i ) 2 Loss =\cfrac{1}{2N}\displaystyle\sum_{i=1}^N(y_{i}-z_{i})^2 Loss=2N1i=1∑N(yi−zi)2
其中zi是网络对第i个样本的预测值:
z i = ∑ j = 0 12 x i j ∗ w j + b z_{i} =\displaystyle\sum_{j=0}^{12}x_{i}^{j}*w_{j}+b zi=j=0∑12xij∗wj+b
梯度的定义:
g r a d i e n t = ( ∂ L ∂ w 0 , ∂ L ∂ w 1 , . . . , ∂ L ∂ w 12 , ∂ L ∂ b ) gradient=(\cfrac{\partial{L}}{\partial{w_{0}}},\cfrac{\partial{L}}{\partial{w_{1}}},...,\cfrac{\partial{L}}{\partial{w_{12}}},\cfrac{\partial{L}}{\partial{b}}) gradient=(∂w0∂L,∂w1∂L,...,∂w12∂L,∂b∂L)
可以计算出L对w和b的偏导数:
∂ L ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ w j = 1 N ∑ i = 1 N ( z i − y i ) x i j \cfrac{\partial{L}}{\partial{w_{j}}}=\cfrac{1}{N}\displaystyle\sum_{i=1}^N(z_{i}-y_{i})\cfrac{\partial{z_{i}}}{\partial{w_{j}}}=\cfrac{1}{N}\displaystyle\sum_{i=1}^N(z_{i}-y_{i})x_{i}^{j} ∂wj∂L=N1i=1∑N(zi−yi)∂wj∂zi=N1i=1∑N(zi−yi)xij
∂ L ∂ b = 1 N ∑ i = 1 N ( z i − y i ) ∂ z i ∂ b = 1 N ∑ i = 1 N ( z i − y i ) \cfrac{\partial{L}}{\partial{b}}=\cfrac{1}{N}\displaystyle\sum_{i=1}^N(z_{i}-y_{i})\cfrac{\partial{z_{i}}}{\partial{b}}=\cfrac{1}{N}\displaystyle\sum_{i=1}^N(z_{i}-y_{i}) ∂b∂L=N1i=1∑N(zi−yi)∂b∂zi=N1i=1∑N(zi−yi)
从导数的计算过程可以看出,因子1/2被消掉了,这是因为二次函数求导的时候会产生因子2,这也是我们将损失函数改写的原因。
将上面计算w和b的梯度的过程,写成Network类的gradient函数,实现方法如下所示。
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
# 调用上面定义的gradient函数,计算梯度
# 初始化网络
net = Network(13)
# 设置[w5, w9] = [-100., -100.]
net.w[5] = -100.0
net.w[9] = -100.0
z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))
point [-100.0, -100.0], loss 686.3005008179159
gradient [-0.850073323995813, -6.138412364807849]
确定损失函数更小的点
下面我们开始研究更新梯度的方法。首先沿着梯度的反方向移动一小步,找到下一个点P1,观察损失函数的变化。
# 在[w5, w9]平面上,沿着梯度的反方向移动到下一个点P1
# 定义移动步长 eta
eta = 0.1
# 更新参数w5和w9
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
# 重新计算z和loss
z = net.forward(x)
loss = net.loss(z, y)
gradient_w, gradient_b = net.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))
point [-99.91499266760042, -99.38615876351922], loss 678.6472185028845
gradient [-0.8556356178645292, -6.0932268634065805]
将上面的循环计算过程封装在train和update函数中,实现方法如下所示。
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights,1)
self.w[5] = -100.
self.w[9] = -100.
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, graident_w5, gradient_w9, eta=0.01):
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
def train(self, x, y, iterations=100, eta=0.01):
points = []
losses = []
for i in range(iterations):
points.append([net.w[5][0], net.w[9][0]])
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
self.update(gradient_w5, gradient_w9, eta)
losses.append(L)
if i % 50 == 0:
print('iter {}, point {}, loss {}'.format(i, [net.w[5][0], net.w[9][0]], L))
return points, losses
3.深度学习平台介绍
近年来深度学习在很多机器学习领域都有着非常出色的表现,在图像识别、语音识别、自然语言处理、机器人、网络广告投放、医学自动诊断和金融等领域有着广泛应用。面对繁多的应用场景,深度学习框架有助于建模者节省大量而繁琐的外围工作,更聚焦业务场景和模型设计本身。
3.1深度学习框架优势
使用深度学习框架完成模型构建有如下两个优势:
1.节省编写大量底层代码的精力:屏蔽底层实现,用户只需关注模型的逻辑结构。同时,深度学习工具简化了计算,降低了深度学习入门门槛。
2.省去了部署和适配环境的烦恼:具备灵活的移植性,可将代码部署到CPU/GPU/移动端上,选择具有分布式性能的深度学习工具会使模型训练更高效。
3.2深度学习框架设计思路
深度学习框架的本质是框架自动实现建模过程中相对通用的模块,建模者只实现模型个性化的部分,这样可以在“节省投入”和“产出强大”之间达到一个平衡。
在构建模型的过程中,每一步所需要完成的任务均可以拆分成个性化和通用化两个部分。
- 个性化部分:往往是指定模型由哪些逻辑元素组合,由建模者完成。
- 通用部分:聚焦这些元素的算法实现,由深度学习框架完成。
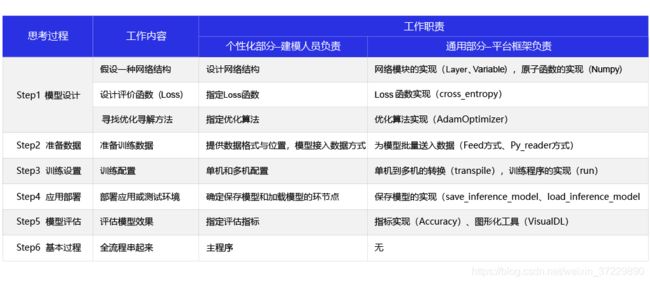
无论是计算机视觉任务还是自然语言处理任务,使用的深度学习模型结构都是类似的,只是在每个环节指定的实现算法不同。因此,多数情况下,算法实现只是相对有限的一些选择,如常见的Loss函数不超过十种、常用的网络配置也就十几种、常用优化算法不超过五种等等。这些特性使得基于框架建模更像一个编写“模型配置”的过程。
3.3飞桨开源深度学习平台
百度出品的深度学习平台飞桨(PaddlePaddle)是主流深度学习框架中一款完全国产化的产品,与Google TensorFlow、Facebook Pytorch齐名。2016 年飞桨正式开源,是国内首个全面开源开放、技术领先、功能完备的产业级深度学习平台。相比国内其他平台,飞桨是一个功能完整的深度学习平台,也是唯一成熟稳定、具备大规模推广条件的深度学习平台。
飞桨源于产业实践,始终致力于与产业深入融合,与合作伙伴一起帮助越来越多的行业完成AI赋能。目前飞桨已广泛应用于医疗、金融、工业、农业、服务业等领域。
飞桨开源深度学习平台全景
飞桨以百度多年的深度学习技术研究和业务应用为基础,集深度学习核心框架、基础模型库、端到端开发套件、工具组件和服务平台于一体,为用户提供了多样化的配套服务产品,助力深度学习技术的应用落地,如 图2 所示。飞桨支持本地和云端两种开发和部署模式,用户可以根据业务需求灵活选择。
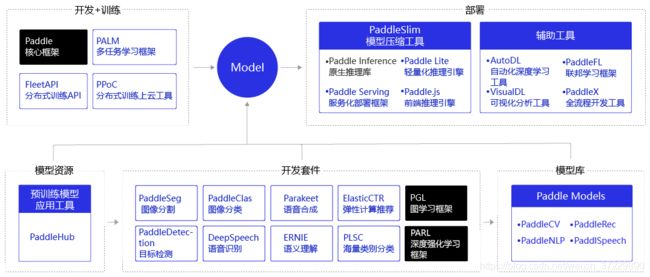
飞桨技术优势
与其他深度学习框架相比,飞桨具有如下四大领先优势:
飞桨快速安装
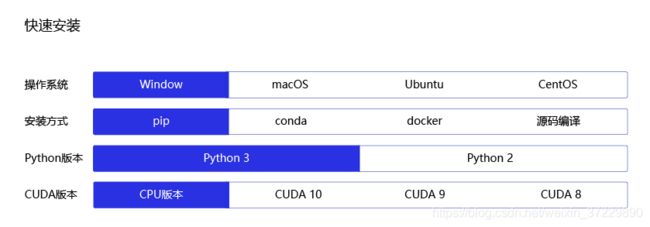
飞桨提供了图形化的安装指导,操作简单,详细步骤请参考 飞桨官网->快速安装。
进入页面后,可按照提示进行安装,如 图9 所示。举例来说,笔者选择在笔记本电脑上安装飞桨,那么选择(windows系统+pip+Python3+CPU版本)的配置组合。其中windows系统和CPU版本是个人笔记本的软硬件配置;Python3是需要事先安装好的Python版本(Python有2和3两个主流版本,两者的API接口不兼容);pip是命令行安装的指令。
4.使用飞桨重写房价预测模型
4.1使用飞桨构建波士顿房价预测模型
在之前的章节中,我们学习使用Python和Numpy构建波士顿房价预测模型的方法,本节我们将尝试使用飞桨重写房价预测模型。在数据处理之前,需要先加载飞桨框架的相关类库。
#加载飞桨、Numpy和相关类库
import paddle
import paddle.fluid as fluid
import paddle.fluid.dygraph as dygraph
from paddle.fluid.dygraph import Linear
import numpy as np
import os
import random
代码中参数含义如下:
- paddle/fluid:飞桨的主库,目前大部分的实用函数均在paddle.fluid包内。
- dygraph:动态图的类库。
- Linear:神经网络的全连接层函数,即包含所有输入权重相加和激活函数的基本神经元结构。在房价预测任务中,使用只有一层的神经网络(全连接层)来实现线性回归模型。
**说明**:
飞桨支持两种深度学习建模编写方式,更方便调试的动态图模式和性能更好并便于部署的静态图模式。
- 静态图模式(声明式编程范式,类比C++):先编译后执行的方式。用户需预先定义完整的网络结构,再对网络结构进行编译优化后,才能执行获得计算结果。
- 动态图模式(命令式编程范式,类比Python):解析式的执行方式。用户无需预先定义完整的网络结构,每写一行网络代码,即可同时获得计算结果。
为了学习模型和调试的方便,本教程均使用动态图模式编写模型。在后续的资深教程中,会详细介绍静态图以及将动态图模型转成静态图的方法。仅在部分场景下需要模型转换,并且是相对容易的。
数据处理
数据处理的代码不依赖框架实现,与使用Python构建房价预测任务的代码相同
def load_data():
# 从文件导入数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算train数据集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 记录数据的归一化参数,在预测时对数据做归一化
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avgs
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
#ratio = 0.8
#offset = int(data.shape[0] * ratio)
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
模型设计
模型定义的实质是定义线性回归的网络结构,飞桨建议通过创建Python类的方式完成模型网络的定义,即定义init函数和forward函数。forward函数是框架指定实现前向计算逻辑的函数,程序在调用模型实例时会自动执行forward方法。在forward函数中使用的网络层需要在init函数中声明。
实现过程分如下两步:
- 定义init函数:在类的初始化函数中声明每一层网络的实现函数。在房价预测模型中,只需要定义一层全连接层,模型结构和《使用Python和Numpy构建神经网络模型》章节模型保持一致。
- 定义forward函数:构建神经网络结构,实现前向计算过程,并返回预测结果,在本任务中返回的是房价预测结果。
class Regressor(fluid.dygraph.Layer):
def __init__(self):
super(Regressor, self).__init__()
# 定义一层全连接层,输出维度是1,激活函数为None,即不使用激活函数
self.fc = Linear(input_dim=13, output_dim=1, act=None)
# 网络的前向计算函数
def forward(self, inputs):
x = self.fc(inputs)
return x
训练配置
- 以guard函数指定运行训练的机器资源,表明在with作用域下的程序均执行在本机的CPU资源上。dygraph.guard表示在with作用域下的程序会以飞桨动态图的模式执行(实时执行)。
- 声明定义好的回归模型Regressor实例,并将模型的状态设置为训练。
- 使用load_data函数加载训练数据和测试数据。
- 设置优化算法和学习率,优化算法采用随机梯度下降SGD,学习率设置为0.01。
训练配置代码如下所示:
# 定义飞桨动态图的工作环境
with fluid.dygraph.guard():
# 声明定义好的线性回归模型
model = Regressor()
# 开启模型训练模式
model.train()
# 加载数据
training_data, test_data = load_data()
# 定义优化算法,这里使用随机梯度下降-SGD
# 学习率设置为0.01
opt = fluid.optimizer.SGD(learning_rate=0.01, parameter_list=model.parameters())
**说明**:
- 默认本案例运行在读者的笔记本上,因此模型训练的机器资源为CPU。
- 模型实例有两种状态:训练状态.train()和预测状态.eval()。训练时要执行正向计算和反向传播梯度两个过程,而预测时只需要执行正向计算。为模型指定运行状态,有两点原因:
(1)部分高级的算子(例如Drop out和Batch Normalization,在计算机视觉的章节会详细介绍)在两个状态执行的逻辑不同。
(2)从性能和存储空间的考虑,预测状态时更节省内存,性能更好。
- 在上述代码中可以发现声明模型、定义优化器等操作都在with创建的 fluid.dygraph.guard()上下文环境中进行,可以理解为with fluid.dygraph.guard()创建了飞桨动态图的工作环境,在该环境下完成模型声明、数据转换及模型训练等操作。
训练过程
训练过程采用二层循环嵌套方式:
- 内层循环: 负责整个数据集的一次遍历,采用分批次方式(batch)。假设数据集样本数量为1000,一个批次有10个样本,则遍历一次数据集的批次数量是1000/10=100,即内层循环需要执行100次。
- 外层循环: 定义遍历数据集的次数,通过参数EPOCH_NUM设置。
batch的取值会影响模型训练效果。batch过大,会增大内存消耗和计算时间,且效果并不会明显提升;batch过小,每个batch的样本数据将没有统计意义。由于房价预测模型的训练数据集较小,我们将batch为设置10。
- 数据准备:将一个批次的数据转变成np.array和内置格式。
- 前向计算:将一个批次的样本数据灌入网络中,计算输出结果。
- 计算损失函数:以前向计算结果和真实房价作为输入,通过损失函数square_error_cost计算出损失函数值(Loss)。飞桨所有的API接口都有完整的说明和使用案例,在后续的资深教程中我们会详细介绍API的查阅方法。
- 反向传播:执行梯度反向传播backward函数,即从后到前逐层计算每一层的梯度,并根据设置的优化算法更新参数opt.minimize。
with dygraph.guard(fluid.CPUPlace()):
EPOCH_NUM = 10 # 设置外层循环次数
BATCH_SIZE = 10 # 设置batch大小
# 定义外层循环
for epoch_id in range(EPOCH_NUM):
# 在每轮迭代开始之前,将训练数据的顺序随机的打乱
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个batch包含10条数据
mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
# 定义内层循环
for iter_id, mini_batch in enumerate(mini_batches):
x = np.array(mini_batch[:, :-1]).astype('float32') # 获得当前批次训练数据
y = np.array(mini_batch[:, -1:]).astype('float32') # 获得当前批次训练标签(真实房价)
# 将numpy数据转为飞桨动态图variable形式
house_features = dygraph.to_variable(x)
prices = dygraph.to_variable(y)
# 前向计算
predicts = model(house_features)
# 计算损失
loss = fluid.layers.square_error_cost(predicts, label=prices)
avg_loss = fluid.layers.mean(loss)
if iter_id%20==0:
print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
# 反向传播
avg_loss.backward()
# 最小化loss,更新参数
opt.minimize(avg_loss)
# 清除梯度
model.clear_gradients()
# 保存模型
fluid.save_dygraph(model.state_dict(), 'LR_model')
保存并测试模型
保存模型
将模型当前的参数数据model.state_dict()保存到文件中(通过参数指定保存的文件名 LR_model),以备预测或校验的程序调用,代码如下所示。
# 定义飞桨动态图工作环境
with fluid.dygraph.guard():
# 保存模型参数,文件名为LR_model
fluid.save_dygraph(model.state_dict(), 'LR_model')
print("模型保存成功,模型参数保存在LR_model中")
理论而言,直接使用模型实例即可完成预测,而本教程中预测的方式为什么是先保存模型,再加载模型呢?这是因为在实际应用中,训练模型和使用模型往往是不同的场景。模型训练通常使用大量的线下服务器(不对外向企业的客户/用户提供在线服务),而模型预测则通常使用线上提供预测服务的服务器,或者将已经完成的预测模型嵌入手机或其他终端设备中使用。因此本教程的讲解方式更贴合真实场景的使用方法。
测试模型
下面我们选择一条数据样本,测试下模型的预测效果。测试过程和在应用场景中使用模型的过程一致,主要可分成如下三个步骤:
- 配置模型预测的机器资源。本案例默认使用本机,因此无需写代码指定。
- 将训练好的模型参数加载到模型实例中。由两个语句完成,第一句是从文件中读取模型参数;第二句是将参数内容加载到模型。加载完毕后,需要将模型的状态调整为eval()(校验)。上文中提到,训练状态的模型需要同时支持前向计算和反向传导梯度,模型的实现较为臃肿,而校验和预测状态的模型只需要支持前向计算,模型的实现更加简单,性能更好。
- 将待预测的样本特征输入到模型中,打印输出的预测结果。
通过load_one_example函数实现从数据集中抽一条样本作为测试样本,具体实现代码如下所示。
def load_one_example(data_dir):
f = open(data_dir, 'r')
datas = f.readlines()
# 选择倒数第10条数据用于测试
tmp = datas[-10]
tmp = tmp.strip().split()
one_data = [float(v) for v in tmp]
# 对数据进行归一化处理
for i in range(len(one_data)-1):
one_data[i] = (one_data[i] - avg_values[i]) / (max_values[i] - min_values[i])
data = np.reshape(np.array(one_data[:-1]), [1, -1]).astype(np.float32)
label = one_data[-1]
return data, label
with dygraph.guard():
# 参数为保存模型参数的文件地址
model_dict, _ = fluid.load_dygraph('LR_model')
model.load_dict(model_dict)
model.eval()
# 参数为数据集的文件地址
test_data, label = load_one_example('./work/housing.data')
# 将数据转为动态图的variable格式
test_data = dygraph.to_variable(test_data)
results = model(test_data)
# 对结果做反归一化处理
results = results * (max_values[-1] - min_values[-1]) + avg_values[-1]
print("Inference result is {}, the corresponding label is {}".format(results.numpy(), label))
通过比较“模型预测值”和“真实房价”可见,模型的预测效果与真实房价接近。房价预测仅是一个最简单的模型,使用飞桨编写均可事半功倍。那么对于工业实践中更复杂的模型,使用飞桨节约的成本是不可估量的。同时飞桨针对很多应用场景和机器资源做了性能优化,在功能和性能上远强于自行编写的模型。
5.学习心得
通过飞桨课程的学习,了解了人工智能、机器学习和深度学习之间的关系,以及发展历程,同时了解了深度学习中神经网络的数据传播过程,用Python和Numpy实现简单的房价预测任务,使我对神经网络的传播过程更加深入的理解。目前学术界和工业界提供的很多便捷的深度学习框架平台,让我们了解了飞桨平台的便捷性和实用性,并且用框架将房价预测模型进行了重写,深刻体会到深度学习平台的易用和方便,在以后的学习中会努力提高自己的理论和编码实践的能力,努力成为一个深度学习领域的专业人才。