深度学习框架——PaddlePaddle 第一周学习笔记
深度学习框架——PaddlePaddle 第一周学习笔记
前言/学习心得
这个暑假,我加入了由百度官方团队打造的《百度架构师手把手带你零基础实践深度学习》课程,里面介绍并教学了他们家的PaddlePaddle深度学习框架。对于AI的学习和生产,目前已经有了许多的框架。知道飞桨的时间并不晚,但真实的接触和认知它却是现在才有的。来自百度的PaddlePaddle于2016年开源,发布了非常多关于人工智能学习的工具。令人惊喜的是,它们的AI studio平台同步跟进了课程、产业、赛事、数据集等多方面同协作的AI内容,这是一个非常完善且流程化的平台。相比于早期的TensorFlow、其高层包装Keras、PyTorch等框架,百度的PaddlePaddle宣称他们在整个AI框架中有着最完整和深入的布局,是实实在在的完成了我国的AI框架。
说实话,作为一个编程小白,甚至不怎么接触python,在花费一点时间再加上群里有着助教以及各种大神,论坛里讨论区的疑问解答的帮助之后,在这第一周也是收获颇丰。
目前,我学会了如何仅用numpy书写房价预测的单层神经网络模型,如何用PaddlePaddle更加简洁地书写房价预测的单层神经网络模型以及目前正在学习的手写数字识别模型等知识
本文主要介绍我学习过程中学习,编写出来的模型的代码,编写的思考过程以及心路历程。
仅用numpy书写房价预测的单层神经网络模型
import numpy as np
import json
import matplotlib.pyplot as plt
#导入数据并进行归一化处理
def load_data():
datafile = 'housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epoches, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epoches):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# 获取数据
train_data, test_data = load_data()
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epoches=50, batch_size=100, eta=0.1)
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
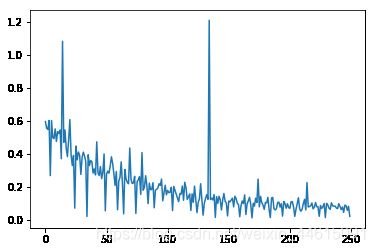
在这个课题中,首先我学习了什么是神经网络,什么是梯度下降法以及什么是随机梯度下降法,并比较了他们两者的优缺点,我们发现,当数据量过大时,随机梯度下降法的收敛速度更快,因此我们一般采用SGD(随机梯度下降)。并且用代码实现了该模型。
用PaddlePaddle更加简洁地书写房价预测的单层神经网络模型
import paddle
import paddle.fluid as fluid
import paddle.fluid.dygraph as dygraph
from paddle.fluid.dygraph import Linear
import numpy as np
def load_data():
# 从文件导入数据
datafile = 'housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算train数据集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 记录数据的归一化参数,在预测时对数据做归一化
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avgs
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
#ratio = 0.8
#offset = int(data.shape[0] * ratio)
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
class Regressor(fluid.dygraph.Layer):
def __init__(self):
super(Regressor, self).__init__()
# 定义一层全连接层,输出维度是1,激活函数为None,即不使用激活函数
self.fc = Linear(input_dim=13, output_dim=1, act=None)
# 网络的前向计算函数
def forward(self, inputs):
x = self.fc(inputs)
return x
# 定义飞桨动态图的工作环境
with fluid.dygraph.guard():
# 声明定义好的线性回归模型
model = Regressor()
# 开启模型训练模式
model.train()
# 加载数据
training_data, test_data = load_data()
# 定义优化算法,这里使用随机梯度下降-SGD
# 学习率设置为0.01
opt = fluid.optimizer.SGD(learning_rate=0.01, parameter_list=model.parameters())
with dygraph.guard(fluid.CPUPlace()):
EPOCH_NUM = 10 # 设置外层循环次数
BATCH_SIZE = 10 # 设置batch大小
# 定义外层循环
for epoch_id in range(EPOCH_NUM):
# 在每轮迭代开始之前,将训练数据的顺序随机的打乱
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个batch包含10条数据
mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
# 定义内层循环
for iter_id, mini_batch in enumerate(mini_batches):
x = np.array(mini_batch[:, :-1]).astype('float32') # 获得当前批次训练数据
y = np.array(mini_batch[:, -1:]).astype('float32') # 获得当前批次训练标签(真实房价)
# 将numpy数据转为飞桨动态图variable形式
house_features = dygraph.to_variable(x)
prices = dygraph.to_variable(y)
# 前向计算
predicts = model(house_features)
# 计算损失
loss = fluid.layers.square_error_cost(predicts, prices)
avg_loss = fluid.layers.mean(loss)
if iter_id%20==0:
print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
# 反向传播
avg_loss.backward()
# 最小化loss,更新参数
opt.minimize(avg_loss)
# 清除梯度
model.clear_gradients()
# 保存模型
fluid.save_dygraph(model.state_dict(), 'LR_model')
在这个课题中,我初步窥见了PaddlePaddle的优势。更加简便的代码书写,更加快速的运行速度。虽然这些在单层神经网络的房价预测模型中并不那么明显,但是可以预见的是,在大型的项目中会有十分惊人的作用。在这次编写的过程中,我逐句对应着原本用numpy书写的模型,这使我对PaddlePaddle有了更深的认知
手写数字识别模型
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Linear
import numpy as np
import random
# 定义mnist数据识别网络结构,同房价预测网络
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义一层全连接层,输出维度是1,激活函数为None,即不使用激活函数
self.fc = Linear(input_dim=784, output_dim=1, act=None)
# 定义网络结构的前向计算过程
def forward(self, inputs):
inputs = fluid.layers.reshape(inputs, (-1, 784))
outputs = self.fc(inputs)
return outputs
# 通过with语句创建一个dygraph运行的context
# 动态图下的一些操作需要在guard下进行
with fluid.dygraph.guard():
model = MNIST()
model.train()
train_loader = paddle.batch(paddle.dataset.mnist.train(), batch_size=1)
imgs = []
labels = []
for batch_id, data in enumerate(train_loader()):
#准备数据,格式需要转换成符合框架要求
image_data = np.array([x[0] for x in data]).astype('float32')
label_data = np.array([x[1] for x in data]).astype('float32').reshape(-1, 1) #reshape中的-1指的是未定值,等待分配,-1相当于一个占位符,为batch_size预留的
imgs.append(image_data)
labels.append(label_data)
len(imgs)
assert len(imgs) == len(labels)
print("length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels)))
# 获得数据集长度
imgs_length = len(imgs)
# 定义数据集每个数据的序号,根据序号读取数据
index_list = list(range(imgs_length))
# 读入数据时用到的批次大小
BATCHSIZE = 100
IMG_ROWS, IMG_COLS = 28,28
def data_generator():
imgs_list = []
labels_list = []
# 随机打乱训练数据的索引序号
random.shuffle(index_list)
for i in index_list:
# 将数据处理成期望的格式,比如类型为float32,shape为[1, 28, 28]
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('float32')
imgs_list.append(img)
labels_list.append(label)
if len(imgs_list) == BATCHSIZE:
# 获得一个batchsize的数据,并返回
yield np.array(imgs_list), np.array(labels_list)
# 清空数据读取列表
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE,
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())
EPOCH_NUM = 10
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(data_generator()):
#准备数据,变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失,取一个批次样本损失的平均值
loss = fluid.layers.square_error_cost(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
手写数字识别模型这章我还没有完全啃透,因为部分代码和学习文档中给出的不太一样,需要自己进行修改,所以作为一个小白的我啃起来就比较慢,不过经过自己的理解还是写出了单层神经网络的手写数字识别模型,后续还需要对模型进行修改与优化。