程设十六周模拟
A - TT数鸭子
问题描述
TT来到一个小湖边,看到了许多在湖边嬉戏的鸭子,TT顿生羡慕。此时他发现每一只鸭子都不一样,或羽毛不同,或性格不同。TT在脑子里开了一个map<鸭子,整数> tong,把鸭子变成了一些数字。现在他好奇,有多少只鸭子映射成的数的数位中不同的数字个数小于k。
Input
输入第一行包含两个数n,k,表示鸭子的个数和题目要求的k。
接下来一行有n个数,ai
ai,每个数表示鸭子被TT映射之后的值。
Output
输出一行,一个数,表示满足题目描述的鸭子的个数。
注意无行末空格
样例输入
6 5
123456789 9876543210 233 666 1 114514
样例输出
4
思路
对于每一个数字,看做一个字符串,判断0-9这十个数字是否出现过,出现+1,>=k就减掉。
代码
#includeB - ZJM要抵御宇宙射线
问题描述
据传,2020年是宇宙射线集中爆发的一年,这和神秘的宇宙狗脱不了干系!但是瑞神和东东忙 于正面对决宇宙狗,宇宙射线的抵御工作就落到了ZJM的身上。假设宇宙射线的发射点位于一个 平面,ZJM已经通过特殊手段获取了所有宇宙射线的发射点,他们的坐标都是整数。而ZJM要构 造一个保护罩,这个保护罩是一个圆形,中心位于一个宇宙射线的发射点上。同时,因为大部分 经费都拨给了瑞神,所以ZJM要节省经费,做一个最小面积的保护罩。当ZJM决定好之后,东东 来找ZJM一起对抗宇宙狗去了,所以ZJM把问题扔给了你~
Input
输入 第一行一个正整数N,表示宇宙射线发射点的个数
接下来N行,每行两个整数X,Y,表示宇宙射线发射点的位置
Output
输出包括两行
第一行输出保护罩的中心坐标x,y 用空格隔开
第二行输出保护罩半径的平方
(所有输出保留两位小数,如有多解,输出x较小的点,如扔有多解,输入y较小的点)
无行末空格
样例输入
5
0 0
0 1
1 0
0 -1
-1 0
样例输出
0.00 0.00
1.0
思路
因为输出的是半径的平方,而输出的x、y都是整数,r^2 =x^2 +y^2,所以输出必然是一个整数。所以直接用longlong。
对于每个点,求出它到所有点的距离中的最大值。找到最大值最小的点即可。
代码
#includeC - 宇宙狗的危机
问题描述
在瑞神大战宇宙射线中我们了解到了宇宙狗的厉害之处,虽然宇宙狗凶神恶煞,但是宇宙狗有一个很可爱的女朋友。
最近,他的女朋友得到了一些数,同时,她还很喜欢树,所以她打算把得到的数拼成一颗树。
这一天,她快拼完了,同时她和好友相约假期出去玩。贪吃的宇宙狗不小心把树的树枝都吃掉了。所以恐惧包围了宇宙狗,他现在要恢复整棵树,但是它只知道这棵树是一颗二叉搜索树,同时任意树边相连的两个节点的gcd(greatest common divisor)都超过1。
但是宇宙狗只会发射宇宙射线,他来请求你的帮助,问你能否帮他解决这个问题
补充知识:
GCD:最大公约数,两个或多个整数共有约数中最大的一个 ,例如8和6的最大公约数是2。
一个简短的用辗转相除法求gcd的例子:
int gcd(int a,int b){return b == 0 ? a : gcd(b,a%b);}
Input
输入第一行一个t,表示数据组数。
对于每组数据,第一行输入一个n,表示数的个数
接下来一行有n个数ai
ai,输入保证是升序的。
Output
每组数据输出一行,如果能够造出来满足题目描述的树,输出Yes,否则输出No。
无行末空格。
样例输入1
1
6
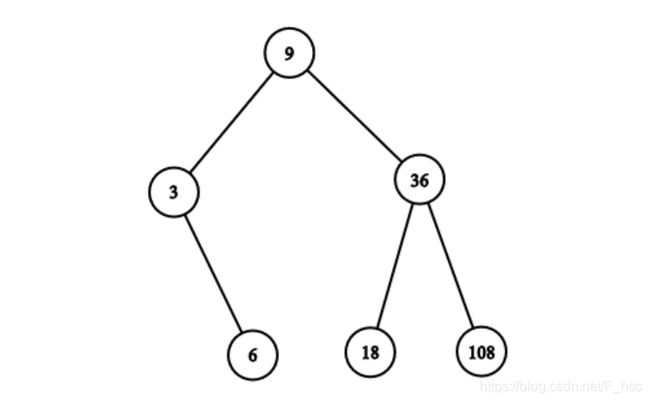
3 6 9 18 36 108
样例输出1
Yes
样例输入2
2
2
7 17
9
4 8 10 12 15 18 33 44 81
样例输出2
No
Yes
样例解释
思路
区间dp
f[i][j]表示i、j之间是否可以连接
dp[i][j][0]表示以j+1为根,i~j作为左子树
dp[i][j][1]表示以i-1为根,i~j作为右子树
在(i,j)中间枚举k,dp[i][j][0]由f[i-1][k]&dp[i][k-1][0]&dp[k+1][r][1]转移,即i-1与k可以建边,(i,k-1)是k的左子树,(k+1,r)是k的右子树,那么就可以建一个以i-1为根,(i,j)为右子树的树。左子树建立同理。
最后判断一下(1,n)可不可以建一棵树。
代码
#include