密码学课程设计之公钥加密RSA

前言

你知道什么叫非对称吗？

正文

简述

RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用；

公钥与私钥的产生

1.随机选择两个不同大质数 p和 q，计算 N=p×q

2.根据欧拉函数，求得r=φ(N)=φ(p)φ(q)=(p−1)(q−1)

3.选择一个小于 r 的整数 e，使 e 和 r互质。并求得 e 关于 r 的模反元素，为 d，有 ed≡1 mod red≡1 mod r

4.将 p 和 q 的记录销毁；

此时，(N,e)是公钥，(N,d)是私钥；

消息加密

首先需要将消息 m 以一个双方约定好的格式转化为一个小于 N，且与 N 互质的整数 n。如果消息太长，可以将消息分为几段，这也就是我们所说的分组加密，后对于每一部分利用如下公式加密：n^e≡c(modN)；

消息解密

利用密钥 d 进行解密：c^d≡n(modN)；

代码分析

生成n字节的随机数

调用os.urandom()随机生成n字节的随机数

def getrandom(n):
	data=urandom(n)
	a=int(binascii.hexlify(data),16)
	return a

第一次素性检验

首先进行第一次素性检验，检验100以内的素数是否为n的因数

def test1(n):
	dic_small=[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]
	# print(len(dic_small))
	for x in dic_small:
		if n%x==0:
			return False
	return True

第二次素性检验

用Miller-rabin素性检验算法检验n，检验k次

def test_Miller(n,k):
	if n<2:
		return False
	d=n-1
	r=0
	while not(d&1):
		r+=1
		d>>=1
	for _ in range(k):
		a=getrandom(120)
		x=pow(a,d,n)
		if x==1 or x==n-1:
			continue
		for _ in range(r-1):
			x=pow(x,2,n)
		if x==1:
			return False
		if x==n-1:
			break
	else:
		return False
	return True

通过两次素性检测

产生byte字节的数，并且通过两次素性检测

def getprime(byte):
	while True:
		n=getrandom(byte)
		if test1(n):
			if test_Miller(n,10):
				pass
			else:
				continue
		else:
			continue
		return n

产生公钥e

产生一个和φ(n)互素的公钥e

def gete(ol):
	e=getprime(1)
	if ol%e!=0:
		return e

16进制编码

加密时，先将明文进行16进制编码，然后转化为10进制计算

def hexencode(str0):
	hexcode=base64.b16encode(str0)
	res=int(hexcode,16)
	return res

16进制解码

解密时需要对计算出来的明文编码进行16进制解码

def hexdecode(str0):
	temp=""
	for i in range(len(str0)):
		if ord(str0[i])>96 and ord(str0[i])<123:
			temp+=chr(ord(str0[i])-32)
		else:
			temp+=str0[i]
	res=base64.b16decode(temp)
	return res

分组加密一组

def RSAencrypt_group(m,e,n):
	num1=hexencode(m)                            
 	c=pow(num1,e,n)                    #cipher
	return c

加密全部

5个字符一组进行加密,将所有的密文连接在一起输出，将每个分组的密文存储在cip列表中用于以后的解密

def RSAencrypt_all(m,e,n):
	res=""
	for i in range(0,len(m),5):
		temp=m[i:i+5]
		group_cipher=RSAencrypt_group(temp,e,n)
		cip.append(group_cipher)
		res+=str(group_cipher)
	return res

解密一组

输入数字c进行RSA解密得到num1，然后再转化为16进制，再对16进制数进行解码变成明文

def RSAdecrypt_group(c,e,n,ol):
	d=gmpy2.invert(e,ol)
	num1=pow(c,d,n)
	str1='{:0x}'.format(num1)
	plain=hexdecode(str1)
	return plain

解密全部

def RSAdecrypt_all(e,n,ol):
	res=""
	for i in range(len(cip)):
		temp=RSAdecrypt_group(cip[i],e,n,ol)
		res+=temp
	return res

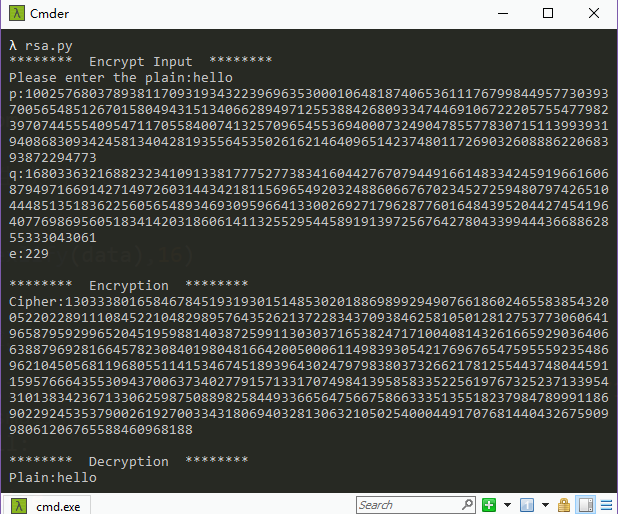
运行结果及正确性验证

理论证明：

即我们要证n^ed≡n(modN)，已知ed≡1modϕ(N)，那么 ed=kϕ(N)+1，即需要证明

n^(kϕ(N)+1)≡n(modN)

这里我们分两种情况证明

第一种情况 gcd(n,N)=1，那么 n^ϕ(N)≡1modN，因此原式成立。

第二种情况 gcd(n,N)!=1，那么 n 必然是 p 或者 q 的倍数，并且 n 小于 N。我们假设n=xp

那么 x 必然小于 q，又由于 q 是素数。那么n^ϕ(q)≡1modq

进而n^kϕ(N)=n^(k(p−1)(q−1))=(n^ϕ(q))^k(p−1)≡1modq

那么n^(kϕ(N)+1)=n+uqn进而nkϕ(N)+1=n+uqxp=n+uxN；所以原式成立。

程序正确性：

程序输入明文hello，加载出1024bit的大素数p和q，继续加载出公钥e，经过加密得到如下密文；就用上面得到的p,q,e,cipher，先计算出私钥d，再解密密文，得到如下明文hello，解密成功，算法正确性得到验证；

安全性分析

RSA 算法的可靠性由极大整数因数分解的难度决定。换言之，对一极大整数做因数分解愈困难，RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今，只有短的 RSA 密钥才可能被强力方式解破，RSA算法选取的两个安全的大素数目前推荐长度为至少为1024比特；到现在为止，还没有任何可靠的攻击 RSA 算法的方式。

RSA的共模攻击分析

攻击原理

当两个用户使用相同的模数 N、不同的私钥时，加密同一明文消息时即存在共模攻击；

设两个用户的公钥分别为 e1和 e2，且两者互质。明文消息为 mm，密文分别为：c1=m^e1(modN) c2=m^e2(modN)

当攻击者截获 c1和 c2后，就可以恢复出明文。用扩展欧几里得算法求出 re1+se2=1modn的两个整数 r 和 s，由此可得：

(c^r1)*(c^s2)≡(m^re1)*(m^se2)modn≡m^(re1+se2)modn≡m(modn)

实例分析

就拿CTF比赛Crypto中的一道题目来说：给出两组密文 message1,message2；给出两组分别的公钥是e1和e2；给出两组加密用的是同一个n；如何去计算出明文呢？

{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,773}
{6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249,839}
message1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
message2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535

可以看出两个公钥的 N 是一样的，并且两者的 e 互素。用上述原理写一个python脚本跑一下：

import gmpy2
n=6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
e1 = 773
e2 = 839
message1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
message2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535
# s & t
gcd, s, t = gmpy2.gcdext(e1, e2)
if s < 0:
    s = -s
    message1 = gmpy2.invert(message1, n)
if t < 0:
    t = -t
    message2 = gmpy2.invert(message2, n)
plain = gmpy2.powmod(message1, s, n) * gmpy2.powmod(message2, t, n) % n
print plain

得出结果明文：

1021089710312311910410111011910111610410511010710511610511511211111511510598108101125

这时候需要考虑当时明文是如何转化为这个数字了，这个应该是 ASCII 字符转换，进而我们使用如下代码得到 flag

i = 0
flag = ""
plain = str(plain)
while i < len(plain):
    if plain[i] == '1':
        flag += chr(int(plain[i:i + 3]))
        i += 3
    else:
        flag += chr(int(plain[i:i + 2]))
        i += 2
print flag

###flag{whenwethinkitispossible}###

有效性和合理性分析

公钥加密中密钥1024bit的密钥强度只能相当于对称加密中几十bit的强度，而且密钥的生成需要时间，所以还是对称加密的效率较高，而且耗时较短，速度比较快；一般通信中采用的就是明文采用对称加密的方法发出，而加解密密钥用公钥加密体制加密后发给接收方，这样效率会比较高；