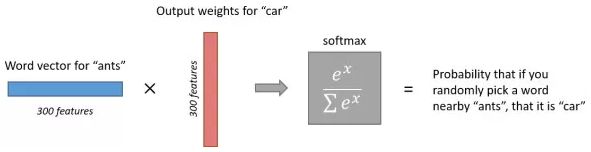
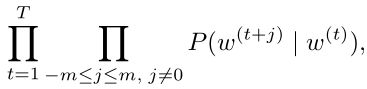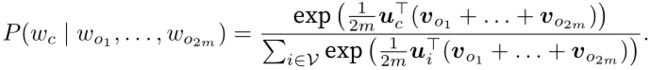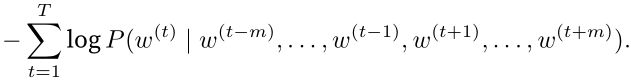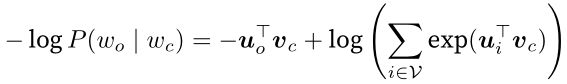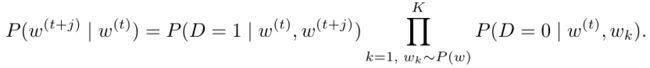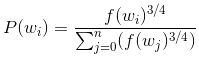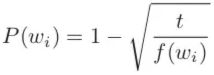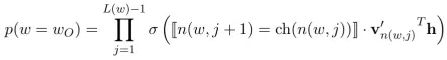词嵌入之Word2vec

one-hot向量的局限性

假设词典大小为N（词典中不同词的数量），每个词可以和从0到N−1的连续整数索引一一对应。使用one-hot方式来表示单词时，词向量维度大小为整个词汇表的大小，改词索引位置为1，其余位置为0，每个词就表示成了一个长度为N的向量，可以直接被神经网络使用。虽然one-hot词向量构造起来很容易，但有两个缺点：

1. 在语料库过大时，词汇表可能达到百万级别，但向量只有一个位置是1，其余的位置全部都是0，这就会导致词向量的长度过大并且是极度稀疏的。
2. one-hot词向量无法准确表达不同词之间的相似度，由于任何两个不同词的one-hot向量的余弦相似度都为0，多个不同词之间的相似度难以通过one-hot向量准确地体现出来。

Word2Vec

把词映射为实数域向量的技术叫词嵌入（word embedding），Word2Vec是解决one-hot表征缺点的一个词嵌入工具。Word2Vec是从大量文本语料中以无监督的方式学习语义知识的一种模型。其核心目标是通过一个嵌入空间将每个词映射到一个空间向量上，它将每个词表示成一个低维度的定长的向量，并且使得语义上相似的单词在该空间内距离很近。并使得这些向量能较好地表达不同词之间的相似和类比关系，不仅存在于语义相似，也存在语法相似。这样词与词之间就可以定量的去度量他们之间的关系，挖掘词之间的联系。由隐特征的表示方式，词向量之间很好地保留了其语义信息，并且这种表示方式没有稀疏的缺点。

如通过Word2Vec的学习，下图将词汇表里的词用Gender，Royal，Age，Food4个维度来表示（在实际情况中，我们并不能对词向量的每个维度做一个很好的解释）。那么可以根据这些的单词所具有的一些属性写出一些特征：，我们希望“国工”和“王子”的数值向量比较接近，而“国王”和“小丑”的数值向量相差较远。数值向量化的操作也能帮助我们得到一些有趣的结论，例如“国王”一“男人”=“女王”一“女人”。

Word2Vec实际是一种浅层的神经网络模型，它有两种网络结构，即跳字模型（Skip-gram）和连续词袋模型（Continues  Bag of Words，CBOW）。CBOW的目标是根据上下文出现的词语来预测当前词的生成概率；Skip-gram是根据当前词来预测上下文中各词的生成概率。

两者都有个共同点就是，input->hidden weights就是我们想要的Embedding权重矩阵，每一行对应一个单词的embedding vector

跳字模型

其思想是在向量空间中，以中心词为输入，最大化上下文单词的相似性。跳字模型假设基于某个词来生成它在文本序列周围的词。举个例子，假设文本序列是“the”“man”“loves”“his”“son”。以“loves”作为中心词，设背景窗口大小为2。跳字模型所关心的是，给定中心词“loves”，生成与它距离不超过2个词的背景词“the”“man”“his”“son”的条件概率，即假设给定中心词的情况下，背景词的生成是相互独立的，那么上式可以改写成

在跳字模型中，每个词被表示成两个d维向量，用来计算条件概率。假设这个词在词典中索引为i，当它为中心词时向量表示为vi，而为背景词时向量表示为ui。设中心词wc在词典中索引为c，背景词wo在词典中索引为o，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

其中词典索引集V={0,1,…,|V|−1}。假设给定一个长度为T的文本序列，设时间步t的词为w(t)。假设给定中心词的情况下背景词的生成相互独立，当背景窗口大小为m时，跳字模型的似然函数即给定任一中心词生成所有背景词的概率

这里小于1和大于T的时间步可以忽略。

训练跳字模型

跳字模型的参数是每个词所对应的中心词向量和背景词向量。训练中我们通过最大化似然函数来学习模型参数，即最大似然估计。这等价于最小化以下损失函数：

如果使用随机梯度下降，那么在每一次迭代里我们随机采样一个较短的子序列来计算有关该子序列的损失，然后计算梯度来更新模型参数。梯度计算的关键是条件概率的对数有关中心词向量和背景词向量的梯度。根据定义，首先看到

通过微分，我们可以得到上式中vc的梯度

它的计算需要词典中所有词以wc为中心词的条件概率。有关其他词向量的梯度同理可得。

训练结束后，对于词典中的任一索引为i的词，我们均得到该词作为中心词和背景词的两组词向量vi和ui。一般使用跳字模型的中心词向量作为词的表征向量。

Skip-gram模型则是利用当前词来预测上下文单词。同样，本文将使用Softmax最为输出层激活函数，这是最基本的模型，使用softmax计算复杂度为O(V)，使用层次softmax或Negative Sampling进行优化，可以将计算复杂度由O(V)降至O(logV) 

朴素Skip-Gram的问题在哪里？问题在于的计算。根据一个词去预测另一个的概率，实际上就是一个多分类问题，多分类问题的输出一般是使用softmax函数来计算的，其输出是一个长度等于类别数的概率向量。对于单词预测，类别数就是词汇表的大小，假设词汇大小为V，单词wi的嵌入表示为zi，那么给定一个中心词w1，预测某一个上下文单词w2的出现概率为：

注意这只是softmax层输出向量中的一个标量而已，完整的softmaxsoftmax层输出为：

不难发现softmax层的计算量非常巨大，因为词汇大小V是巨大的。

 

Skip-gram模型分为建立模型和通过模型获取嵌入词向量两个部分。先基于训练数据构建一个神经网络，训练模型获得模型基于训练数据学得的隐层权重矩阵。

如何来把这些训练样本输入模型呢?首先，我们都知道神经网络只能接受数值输入，我们不可能把一个单词字符串作为输入，因此我们得想个办法来表示这些单词。最常用的办法就是基于训练文档来构建我们自己的词汇表（vocabulary），再对单词进行one-hot编码。假设从我们的训练文档中抽取出L0000个唯一不重复的单词组成词汇表。我们对这10000个单词进行one-hot编码，得到的每个单词都是一个10000维的向量，向量每个维度的值只有0或者1。观察Skih-Cram模型的输入如果为一个10000维的向量.那么输出也是一个10000维词汇表的大小)的向量，它包含了10000个概率，每一个概率代表着当前词是输入样本中output word的概率大小。最终模型的输出是一个概率分布

如果我们现在想用300个特征来表示一个单词(每个单词可以被表示为300维的向量)。那么隐藏层的权重矩阵应该为10000行，300列(隐藏层有300个节点)。这300列的向量就对应了我们输入单词的词向量。
模型的输出是一个概率分布，基于大量的语料数据，“国王”和“王子”前后的词出现的概率比较接近，所以训练得到的词向量也会比较接近，所以“国王”和“王子”的数值向量比较接近，而“国王”和“小丑”的数值向量相差较远。

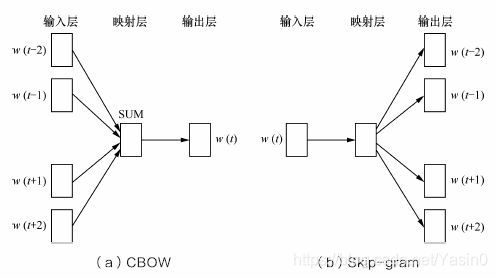
其中w(t)是当前所关注的词，w(t−2)、w(t−1)、w(t+1)、w(t+2)是上下文中出现的词。这里前后滑动窗口大小均设为2。

CBOW和Skip-gram都可以表示成由输入层（Input）、映射层（Projection）和输出层（Output）组成的神经网络。
输入层中的每个词由独热编码方式表示，在映射层（又称隐含层）中，K个隐含单元的取值可以由N维输入向量以及连接输入和隐含单元之间的N×K维权重矩阵计算得到。在CBOW中，还需要将各个输入词所计算出的隐含单元求和。同理，输出层向量的值可以通过隐含层向量（K维），以及连接隐含层和输出层之间的K×N维权重矩阵计算得到。输出层也是一个N维向量，每维与词汇表中的一个单词相对应。最后，对输出层向量应用Softmax激活函数，可以计算出每个单词的生成概率。Softmax激活函数的定义为

其中x代表N维的原始输出向量，x n 为在原始输出向量中，与单词w n 所对应维度的取值。
接下来的任务就是训练神经网络的权重，使得语料库中所有单词的整体生成概率最大化。从输入层到隐含层需要一个维度为N×K的权重矩阵，从隐含层到输出层又需要一个维度为K×N的权重矩阵，学习权重可以用反向传播算法实现，每次迭代时将权重沿梯度更优的方向进行一小步更新。但是由于Softmax激活函数中存在归一化项的缘故，推导出来的迭代公式需要对词汇表中的所有单词进行遍历，使得每次迭代过程非常缓慢，由此产生了Hierarchical  Softmax和NegativeSampling两种改进方法，训练得到维度为N×K和K×N的两个权重矩阵之后，可以选择其中一个作为N个词的K维向量表示。

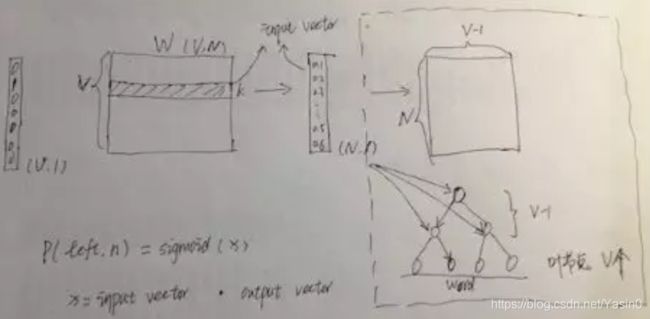
Skip-gram是指根据一个当前词预测多个上下文单词，是一对多的关系。 下图并不是网络结构，只是示意图：

需要注意：

1. 输出是当前单词的one hot向量。跟CBOW一样，input -> hidden weights就是Embedding矩阵，V行N列，每一行对应字典中一个单词的嵌入向量，在Word2Vec中也叫做输入单词的input vector；中间隐藏层到输出层共享权重矩阵W‘ shape=(N,V)，注意与input -> hidden权重矩阵是两个不同的矩阵。W’中每一列也对应一个单词，被称为该单词的output vector；
2. 中间隐藏层没有激活函数，只是线性投影；
3. 输出层将input vector和output vector进行点乘，然后使用softmax进行归一化，就得到了在当前单词输入下，输出是对应单词的概率；
4. Skip-gram在训练的时候，每一个训练样本都是一对单词，输入输出都只是一个单词，其网络结构和CBOW中one context的网络结构是相同的。

可能有小伙伴又问了，既然同一个中心词，权重矩阵W W‘也没有发生变化（共享的），那么是不是针对不同的上下文单词训练样本，每一次网络的输出向量都是一样的那？而上下文单词又是不同的，这难道不会给模型的学习带来混乱吗（到底想让模型输出什么那）？训练完之后，输入中心词，模型又会预测哪个上下文单词那？

先放答案：

1. 同一个中心词，权重是不变的，针对不同上下文单词，网络每次输出向量当然是相同的；但是在论文给出的实现代码中，每一个训练样本之后都会更新一次权重，所以权重不是不变的哦

2. 不会给网络造成混乱。因为模型的目标函数是将整体的交叉熵降到最低，模型会找到一个中间的平衡点，使得loss最低

3. 训练完之后，输入中心词，输出单词跟语料中每个单词的统计次数有关。虽然同一个中心词对应不同的上下文，但是有的上下文单词出现的多，有的出现的少，它们会影响loss的计算。毫无疑问，为了降低loss，模型倾向于预测出现较多的上下文单词。其实并不不关心预测哪个单词，关心的只是使得loss最小的训练后模型的input -> hidden权重。

---

连续词袋模型

连续词袋模型与跳字模型类似。与跳字模型最大的不同在于，连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。在同样的文本序列“the”“man”“loves”“his”“son”里，以“loves”作为中心词，且背景窗口大小为2时，连续词袋模型关心的是，给定背景词“the”“man”“his”“son”生成中心词“loves”的条件概率，也就是

连续词袋模型关心给定背景词生成中心词的条件概率

因为连续词袋模型的背景词有多个，我们将这些背景词向量取平均，然后使用和跳字模型一样的方法来计算条件概率。设vi和ui分别表示词典中索引为ii的词作为背景词和中心词的向量（注意符号的含义与跳字模型中的相反）。设中心词wcwc在词典中索引为c，背景词wo1,…,wo2m在词典中索引为o1,…,o2m，那么给定背景词生成中心词的条件概率

为了让符号更加简单，我们记，且，那么上式可以简写成

给定一个长度为T的文本序列，设时间步tt的词为w(t)，背景窗口大小为m。连续词袋模型的似然函数是由背景词生成任一中心词的概率

训练连续词袋模型

训练连续词袋模型同训练跳字模型基本一致。连续词袋模型的最大似然估计等价于最小化损失函数

注意到

通过微分，我们可以计算出上式中条件概率的对数有关任一背景词向量voi（i=1,…,2m）的梯度

有关其他词向量的梯度同理可得。同跳字模型不一样的一点在于，我们一般使用连续词袋模型的背景词向量作为词的表征向量。

小结

• 词向量是用来表示词的向量。把词映射为实数域向量的技术也叫词嵌入。
• word2vec包含跳字模型和连续词袋模型。跳字模型假设基于中心词来生成背景词。连续词袋模型假设基于背景词来生成中心词。

CBOW模型

CBOW全称是Continuous Bag Of Words, 是指利用上下文单词来预测一个词。这个上下文可以只有上文/下文，也可以上下文都有。具体是多长的上下文，是人为指定的，也称为窗口大小。

CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量，而输出就是这特定的一个词的词向量。比如上下文大小取值为4，共有8个词作为模型的输入，输出词向量是"Learning"。由于CBOW使用的是词袋模型，抛弃了词序信息，不考虑他们和我们关注的词之间的距离大小。

这个CBOW的例子里，输入是8个词向量，输出是所有词的softmax概率（训练的目标是期望训练样本特定词对应的softmax概率最大），对应的CBOW神经网络模型输入层有8个神经元，输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法，可以求出DNN模型的参数，同时得到所有的词对应的词向量。这样当我们有新的需求，要求出某8个词对应的最可能的输出中心词时，我们可以通过一次DNN前向传播算法并通过softmax激活函数找到概率最大的词对应的神经元即可。

Skip-Gram模型输入是特定的一个词的词向量，而输出是特定词对应的上下文词向量。

输入是特定词， 输出是softmax概率排前8的8个词，对应的Skip-Gram神经网络模型输入层有1个神经元，输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法，我们可以求出DNN模型的参数，同时得到所有的词对应的词向量。这样当我们有新的需求，要求出某1个词对应的最可能的8个上下文词时，我们可以通过一次DNN前向传播算法得到概率大小排前8的softmax概率对应的神经元所对应的词即可。

word2vec主要是为了解决DNN模型的这个处理过程非常耗时。我们的词汇表一般在百万级别以上，这意味着我们DNN的输出层需要进行softmax计算各个词的输出概率的的计算量很大。 

输入层:n个节点（one-hot向量的维度），上下文共2 x 滑动窗口个词的词向量的平均值，即上下文2 x 滑动窗口个词的one-liot-representation;
    输入层到输出层的连接边:输出i司矩阵
    输出层:|V|个节点。第i个节点代表中心词是词Wi的概率。

给出当前上下文（只有一个词），求出下一个词是字典中的某个词的概率，概率有大有小，最大的那个就是模型预测出来的下一个词。为了保证这个词真的是语料中下一个词，我们需要调整概率分布使得其概率最大。V是词典中word的数量，N表示词向量的维度/嵌入的维度。

 

输入是多个one hot形式的V维度向量，他们使用同一个input -> hidden layer权重矩阵，选出其中对应的行。然后对其取平均值作为中间隐藏层的输出。中间有一个嵌入维度为N的隐藏层（没有激活函数），输出V维向量（使用softmax激活函数）。
因为onehot向量只有一个非零值且为1，其与任何矩阵相乘起到的是一个查询某行的作用。当使用一个词的onehot向量与嵌入矩阵相乘时（输入到隐藏层的权重矩阵），其实就相当于取出嵌入矩阵的某一行，这输入单词的词的嵌入向量，维度为N。最终想要的就是input -> hidden layer的权重矩阵，矩阵shape=(V,N)，每一行都是一个N维向量，就是对应位置的词向量。

hidden->output layer 矩阵是另外一个矩阵，它完成从隐藏层到输出层的映射。 W’中每一列依次与h相乘，就对应着输出层中每一个神经元的值，而输出层的每一个神经元对应着一个单词。如下图所示。

所以W'每一列也对应着字典中一个单词，我们称该列为对应单词的output vector，维度为N。

CBOW与Skip-gram的区别：

1. CBOW是利用上下文预测中心词，Skip-gram是利用中心词预测上下文

2. Skip-gram效果比CBOW好。 

3. Skip-gram训练时间长，但是对低频词(生僻词)效果好；CBOW训练时间短，对低频词效果比较差。

关于第三点多深挖一下，为什么会这样那？

CBOW是利用上下文预测中心词，训练过程是从输出的中心词的loss来学习上下文的词向量。V个中心词，对应V个训练样本，一共学习V次就结束了。训练复杂度O(V)，训练时间较快。而且上下文词向量是取得平均值，一视同仁的对待，那么低频词训练的少，而且也没有特殊处理，当然效果不好。

Skip-gram利用中心词预测上下文，假设我们考虑前后共K个上下文，那么每一个上下文都会修正一次中心词的词向量表达，训练复杂度是O(KV)训练时间会变长。但是低频词也有多个上下文，相比于CBOW，其词向量会被多次修正，自然效果也就好一些。

在通俗一点来讲，CBOW是一个老师多个学生，每个学生平等对待，学生能学多少，看你上了多少次老师的课（作为上下文被修正了多少次）。Skip-gram是多个老师一个学生，即使这个学生出现的次数很少，但是每次上课都是多个老师在教他，自然就学的多，从整个训练的角度来看，自然花费的时间也就长，毕竟每个学生都要被多个老师教一遍。

---

近似训练

回忆上一节的内容。跳字模型的核心在于使用softmax运算得到给定中心词wc来生成背景词wo的条件概率

该条件概率相应的对数损失

由于softmax运算考虑了背景词可能是词典VV中的任一词，以上损失包含了词典大小数目的项的累加。在上一节中我们看到，不论是跳字模型还是连续词袋模型，由于条件概率使用了softmax运算，每一步的梯度计算都包含词典大小数目的项的累加。对于含几十万或上百万词的较大词典，每次的梯度计算开销可能过大。为了降低该计算复杂度，本节将介绍两种近似训练方法，即负采样（negative sampling）或层序softmax（hierarchical softmax）。由于跳字模型和连续词袋模型类似，本节仅以跳字模型为例介绍这两种方法。

负采样

负采样修改了原来的目标函数。给定中心词wc的一个背景窗口，我们把背景词wo出现在该背景窗口看作一个事件，并将该事件的概率计算为，其中的σ函数与sigmoid激活函数的定义相同

我们先考虑最大化文本序列中所有该事件的联合概率来训练词向量。具体来说，给定一个长度为T的文本序列，设时间步tt的词为w(t)且背景窗口大小为m，考虑最大化联合概率

然而，以上模型中包含的事件仅考虑了正类样本。这导致当所有词向量相等且值为无穷大时，以上的联合概率才被最大化为1。很明显，这样的词向量毫无意义。负采样通过采样并添加负类样本使目标函数更有意义。设背景词wowo出现在中心词wcwc的一个背景窗口为事件PP，我们根据分布P(w)P(w)采样KK个未出现在该背景窗口中的词，即噪声词。设噪声词wk（k=1,…,K）不出现在中心词wc的该背景窗口为事件Nk。假设同时含有正类样本和负类样本的事件P,N1,…,NK相互独立，负采样将以上需要最大化的仅考虑正类样本的联合概率改写为

其中条件概率被近似表示为

设文本序列中时间步tt的词w(t)在词典中的索引为it，噪声词wk在词典中的索引为hk。有关以上条件概率的对数损失为

现在，训练中每一步的梯度计算开销不再与词典大小相关，而与KK线性相关。当KK取较小的常数时，负采样在每一步的梯度计算开销较小。

 

Negative Sampling

Skip-Gram模型的思路是使用一个中心词去预测上下文词，word2vec将其转成了预测两个单词是否具有上下文关系，即把无监督多分类问题转成了有监督二分类问题。解决extreme multiclass问题所用到的技术叫负采样(negative sampling)。

假设文本数据中有这么一段：

… a glass of orange juice …

假设以orange为中心词，窗口为1，那么能得到一个正样本

[(orange, juice), 1]

这里暂时不考虑[orange, of]。假设负采样率k=3，那么在词汇中取出3个与orange无上下文关系的单词组成三个负样本：

[(orange, king), 0]

[(orange, book), 0]

[(orange, boy), 0]

那么现在现在只需要计算k+1个概率：

在该轮只需要把这四个输出当做是四个二分类器来更新参数即可。损失函数可以写成：

其中D代表词组对的关系，如果两单词具有上下文关系则D=1，反之D=0；pairpos代表正样本单词对，pairneg代表负样本单词对；N表示样本数。

那么如何选取单词区构成负样本？原论文中给出的建议是，在生成负样本时，单词wi被选中的概率为：

其中f(wi)表示单词wi在整个文本数据中出现的频数；|V|表示词汇大小。

 

Negative Sampling

Negative Sampling（简称NEG）是NCE（Noise Contrastive Estimation）的简化版本，目的是提高训练速度并改善所得词向量的质量。与Hierarchical Softmax相比，NEG不再采用复杂的霍夫曼树，而是利用相对简单的随机负采样，能大幅提升性能，因而可以作为Hierarchical Softmax的一种替代。

针对一个样本(WI, W)，Negative Sampling的目标函数如下所示：

现在的目标就是利用logistic regression，从带有噪声（负样本）的目标中找到正样本（Wo），其中K是负样本采样的数量。作者指出在小训练集上，k取5-20比较合适；大训练集上k取2-5即可。和SGD的思想非常像，不再是利用所有的负样本进行参数的更新，而是只利用负采样出来的K个来进行loss的计算，参数的更新。只不过SGD每次只用一个样本，而不是K个。

负样本采样服从分布Pn(W)，经过试验发现unigram分布效果最好，如下：

其中f(wi)表示单词wi在语料中出现的频率。3/4这个值是通过实验发现的经验值。

Subsampling of Frequent Wrods

大语料集中，像the a in之类的单词出现频率非常高几乎是很多单词的上下文，造成其携带的信息非常少。对这些单词进行下采样不仅可以加快训练速度还可以提高低频词训练词向量的质量。

为了平衡高频与低频词，对训练集中的单词按照下述公式决定是否保留该单词：

其中f(wi)是单词wi出现的频率，t凭经验值取10的-5次方。该公式保证出现频率超过t的单词将被下采样，并且不会影响原有的单词的频率相对大小（rank）。先生成（target， context），比如（love，[ I,China]），然后依次遍历他们，小于P(wi)的训练样本将被从训练样本中去掉。

词组Phrases

词组并不能简单的将单词分开解释，而是应该看做一个整体，例如“New York”。把这样的词组看成是一个整体，用特殊的符号代替不会过多的增加词汇表的大小，但效果是很显著的。

---

层序softmax

层序softmax是另一种近似训练法。它使用了二叉树这一数据结构，树的每个叶结点代表词典VV中的每个词。

图 10.3 层序softmax。二叉树的每个叶结点代表着词典的每个词

假设L(w)为从二叉树的根结点到词ww的叶结点的路径（包括根结点和叶结点）上的结点数。设n(w,j)为该路径上第jj个结点，并设该结点的背景词向量为un(w,j)。以图10.3为例，L(w3)=4。层序softmax将跳字模型中的条件概率近似表示为

其中σ函数sigmoid激活函数，leftChild(n)是结点nn的左子结点：如果判断xx为真，[[x]]=1；反之[[x]]=−1。 让我们计算图10.3中给定词wc生成词w3的条件概率。我们需要将wcwc的词向量vc和根结点到w3路径上的非叶结点向量一一求内积。由于在二叉树中由根结点到叶结点w3的路径上需要向左、向右再向左地遍历（图10.3中加粗的路径），我们得到

由于σ(x)+σ(−x)=1，给定中心词wc生成词典V中任一词的条件概率之和为1这一条件也将满足：

此外，由于L(wo)−1的数量级为O(log2|V|)，当词典V很大时，层序softmax在训练中每一步的梯度计算开销相较未使用近似训练时大幅降低。

小结

• 负采样通过考虑同时含有正类样本和负类样本的相互独立事件来构造损失函数。其训练中每一步的梯度计算开销与采样的噪声词的个数线性相关。
• 层序softmax使用了二叉树，并根据根结点到叶结点的路径来构造损失函数。其训练中每一步的梯度计算开销与词典大小的对数相关。

word2vec

为了优化Skip-Gram在计算softmax时的计算负担，word2vec提出了两种优化方法：Hierarchical Softmax与Negative Sampling。层次Softmax与负采样策略

Hierarchical Softmax

word2vec也使用了CBOW与Skip-Gram来训练模型与得到词向量，但是并没有使用传统的DNN模型。最先优化使用的数据结构是用霍夫曼树来代替隐藏层和输出层的神经元，霍夫曼树的叶子节点起到输出层神经元的作用，叶子节点的个数即为词汇表的小大。 而内部节点则起到隐藏层神经元的作用。

一次性平行地计算所有单词的概率值然后取最大概率太低效，那么可以使用分层的思想来计算概率。如果使用一颗平衡二叉树，每个叶节点代表一个单词，那么找到目标单词只需要计算从root到leaf的一条路径，计算复杂度就可以从V降低到log2V。把所有单词映射到二叉树的叶节点上，目标是找到最有可能出现的目标单词。

Hierarchical Softmax把神经网络的full softmax层转成了一个树形结构，该树的每个叶子节点代表一个词，该树的结构采用根据词频生成的霍夫曼树。

每个非叶节点即是一个神经元，其权重参数为θi。假设wi是一个中心词，w2是其一个上下文单词，那么根节点的输入为wi的嵌入向量zi，那么计算P(w2|wi)需要经过一条路径：

在Hierarchical Softmax训练过程中，期望最大化P(w2|wi)就只需要计算一条路径即可，计算复杂度的期望值为log2V，同样通过梯度下降法来优化。

Hierarchical Softmax

原始的Word2Vec使用softmax得到最种的词汇概率分布，词汇表往往包含上百万个单词，如果针对输出中每一个单词都要用softmax计算概率的话，计算量是非常大的。解决办法之一就是Hierarchical Softmax。相比于原始的Softmax直接计算每个单词的概率，Hierarchical Softmax使用一颗二叉树来得到每个单词的概率。被验证的效果最好的二叉树类型就是霍夫曼树：

霍夫曼树中有V-1个中间节点，V个叶节点。叶节点与单词表中V个单词一一对应。首先根据单词出现的频率构造一颗霍夫曼树，出现频率高的单词霍夫曼编码就短，更加靠近根节点。
原来的Word2Vec模型结构会被改变，隐藏层后直接和霍夫曼树中每一个非叶节点相连，如下图所示（相当于输出层中只有V-1个神经元节点）。然后再每一个非叶节点上计算二分概率（也就是用Sigmoid函数进行激活），这个概率是指从当前节点随机游走的概率，可以任意指定是向左游走的概率，还是向右游走的概率。从根节点到目标单词的路径是唯一的，将中间非叶节点的游走概率相乘就得到了最终目标单词的概率。

这样只用计算树深度个输出节点的概率就可以得到目标单词的概率。霍夫曼树的深度基本是logV，所以此时的计算复杂度就降为了O(logV)。另外，高频词非常接近树根，其所需要的计算次数将进一步减少，这也是使用霍夫曼树的一个优点。此时的目标函数为：

L(w)是树深度；n(w,j)表示从根节点到目标单词w的路径上第j个节点；ch(n)表示节点n的孩子节点。中间的尖括号表示是否成立的判断，结果无非是+1，或-1。注意sigmoid的特性：
Sigmoid(-x) = 1 - Sigmoid(x)
Vwi表示输入单词的input vector，Vn’表示霍夫曼树中间节点的output vector。

---

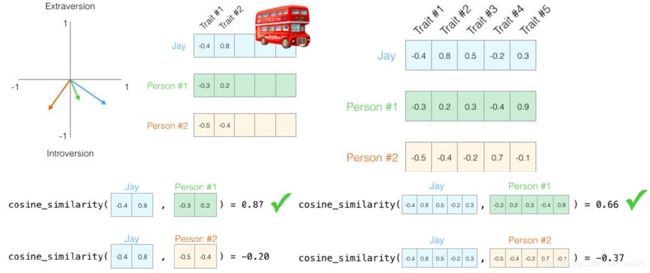
一个人的个性的向量表示中获得了很多有用的信息。代表了我的个性。比较中使用所有五个维度：处理向量时，计算相似度得分的常用方法是余弦相似度：一号人物与我的余弦相似度得分高，所以我们的性格比较相似。

 

使用滑动窗口产生样本：

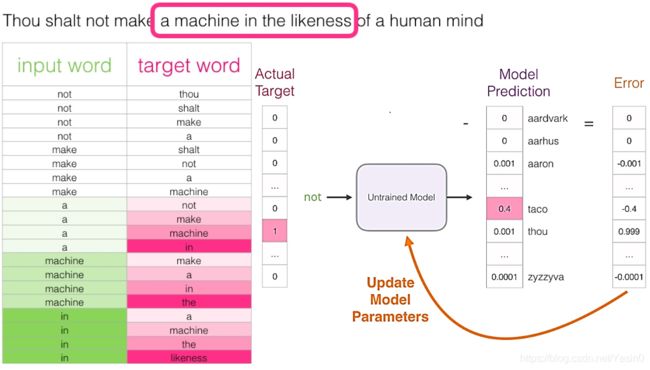
现在我们已经从现有的运行文本中提取了我们的skipgram训练数据集，让我们看看我们如何使用它来训练预测相邻单词的基本神经语言模型。我们从数据集中的第一个样本开始。我们把特征提供给未经训练的模型，要求它预测一个合适的相邻单词。

 

该模型进行三个步骤并输出预测向量（概率分配给其词汇表中的每个单词）。由于该模型未经过训练，因此在此阶段的预测肯定是错误的。但那没关系。我们知道应该它将猜到哪个词：我们目前用于训练模型的行中的标签/输出单元格：

“目标向量”的词（字）概率为1，其他词（字）的概率都是0。我们减去两个向量，得到一个误差向量：
现在可以使用此误差向量来更新模型，以便下次当“not”作为输入时，模型更有可能猜测“thou”。

 

这就是训练的第一步。我们继续使用数据集中的下一个样本进行相同的处理，然后是下一个样本，直到我们覆盖了数据集中的所有样本。这就结束了一个epcho的训练。我们继续训练多个epcho，然后我们就有了训练好的模型，我们可以从中提取嵌入矩阵并将其用于任何其他应用。这加深了我们对该过程的理解，但仍然不是word2vec实际上的训练过程。

负采样
从计算的角度来看，第三步非常消耗资源：尤其是我们将在数据集中为每个训练样本做一次（很可能数千万次）。
一种方法是将目标分成两个步骤：

1. 生成高质量的单词嵌入（不要担心下一个单词预测）。
2. 使用这些高质量的嵌入来训练语言模型（进行下一个单词预测）。

我们将专注于第1步，因为我们专注于嵌入。要使用高性能模型生成高质量嵌入，我们可以从预测相邻单词切换模型的任务：

并将其切换到一个取输入和输出字的模型，并输出一个分数，表明它们是否是邻居（0表示“不是邻居”，1表示“邻居”）。

这个简单的改变，将我们需要的模型从神经网络改为逻辑回归模型：因此它变得更简单，计算速度更快。
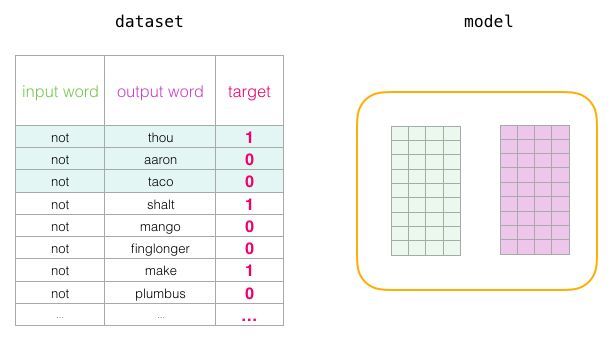
这个改变要求我们切换数据集的结构 - 标签现在是一个值为0或1的新列。它们将全部为1，因为我们添加的所有单词都是邻居。

现在可以以极快的速度计算 - 在几分钟内处理数百万个示例。但是我们需要关闭一个漏洞。如果我们所有的例子都是正面的（目标：1），我们打开自己的智能模型的可能性总是返回1 - 达到100％的准确性，但什么都不学习并生成垃圾嵌入。

为了解决这个问题，我们需要在数据集中引入负样本 - 不是邻居的单词样本。我们的模型需要为这些样本返回0。现在这是一个挑战，模型必须努力解决，而且速度还要快。

图：对于我们数据集中的每个样本，我们添加了负样本。它们具有相同的输入词和0标签。但是我们填写什么作为输出词？我们从词汇表中随机抽取单词

将实际信号（相邻单词的正例）与噪声（随机选择的不是邻居的单词）进行对比。这是计算量和统计效率的巨大折衷。

Word2vec训练流程

现在我们已经建立了skipgram和负采样的两个中心思想，我们可以继续仔细研究实际的word2vec训练过程。
在训练过程开始之前，我们预先处理我们正在训练模型的文本。在这一步中，我们确定词汇量的大小（我们称之为vocab_size，比如说，将其视为10,000）以及哪些词属于它。 在训练阶段的开始，我们创建两个矩阵 - Embedding矩阵和Context矩阵。这两个矩阵在我们的词汇表中嵌入了每个单词（这vocab_size是他们的维度之一）。 第二个维度是我们希望每次嵌入的时间长度（embedding_size- 300是一个常见值，但我们在本文前面的例子是50。）。

在训练过程开始时，我们用随机值初始化这些矩阵。然后我们开始训练过程。在每个训练步骤中，我们采取一个正样本及其相关的负样本。我们来看看我们的第一组：

现在我们有四个单词：输入单词not和输出/上下文单词:( thou实际邻居）,aaron，和taco（负样本）。我们继续查找它们的嵌入 - 对于输入词，我们查看Embedding矩阵。对于上下文单词，我们查看Context矩阵（即使两个矩阵都在我们的词汇表中嵌入了每个单词）。

然后，我们计算输入嵌入与每个上下文嵌入的点积。。在每种情况下，会产生一个数字，该数字表示输入和上下文嵌入的相似性。现在我们需要一种方法将这些分数转化为看起来像概率的东西 ：使用sigmoid函数把概率转换为0和1。
现在我们可以将sigmoid操作的输出视为这些样本的模型输出。您可以看到taco得分最高aaron，并且在sigmoid操作之前和之后仍然具有最低分。 既然未经训练的模型已做出预测，并且看到我们有一个实际的目标标签要比较，那么让我们计算模型预测中的误差。为此，我们只从目标标签中减去sigmoid分数。error=target−sigmoid
这是“机器学习”的“学习”部分。现在，我们可以利用这个错误分数调整not，thou，aaron和taco的嵌入,使下一次我们做出这一计算，结果会更接近目标分数。

训练步骤到此结束。我们从这一步骤中得到稍微好一点的嵌入（not，thou，aaron和taco）。我们现在进行下一步（下一个正样本及其相关的负样本）,并再次执行相同的过程。

当我们循环遍历整个数据集多次时，嵌入继续得到改进。然后我们可以停止训练过程，丢弃Context矩阵，并使用Embeddings矩阵作为下一个任务的预训练嵌入。

窗口大小和负样本数量
word2vec训练过程中的两个关键超参数是窗口大小和负样本的数量。

不同的窗口大小可以更好地提供不同的任务。
一种启发式方法是较小的窗口嵌入（2-15），其中两个嵌入之间的高相似性得分表明这些单词是可互换的（注意，如果我们只查看周围的单词，反义词通常可以互换 - 例如，好的和坏的经常出现在类似的情境中）。
使用较大的窗口嵌入（15-50，甚至更多）会得到相似性更能指示单词相关性的嵌入。实际上，您通常需要对嵌入过程提供注释指导，为您的任务带来有用的相似感。
Gensim默认窗口大小为5（输入字本身加上输入字之前的两个字和输入字之后的两个字）。

负样本的数量是训练过程的另一个因素。原始论文里负样本数量为5-20。它还指出，当你拥有足够大的数据集时，2-5似乎已经足够了。Gensim默认为5个负样本。

层次softmax的执行流程、公式推导层次softmax、为什么建哈夫曼树，哈夫曼树的建立、霍夫曼树的伪代码，负采样、时间复杂度的分析，样本不均衡的处理，损失函数 ？word2vec的输入输出层是什么样的？

博客

1. CBOW与Skip-gram比较      https://zhuanlan.zhihu.com/p/37477611
2. Hierarchical softmax and negative sampling: short notes worth telling  
3. https://towardsdatascience.com/hierarchical-softmax-and-negative-sampling-short-notes-worth-telling-2672010dbe08
4. [ Word embeddings: exploration, explanation, and exploitation (with code in Python)]
5. https://towardsdatascience.com/word-embeddings-exploration-explanation-and-exploitation-with-code-in-python-5dac99d5d795
6. [ Word2Vec Tutorial - The Skip-Gram Model ]      http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/
7. [ Word2Vec Tutorial Part 2 - Negative Sampling ]http://mccormickml.com/2017/01/11/word2vec-tutorial-part-2-negative-sampling/
8. [秒懂词向量Word2Vec的本质]   https://zhuanlan.zhihu.com/p/26306795
9. [ A Beginner's Guide to Word2Vec and Neural Word Embeddings ]  https://skymind.ai/wiki/word2vec
10. 一个正儿八经的word2vec示例见此。
11. https://blog.csdn.net/itplus/article/details/37969519
12. https://daya-jin.github.io/2019/02/02/WordEmbedding