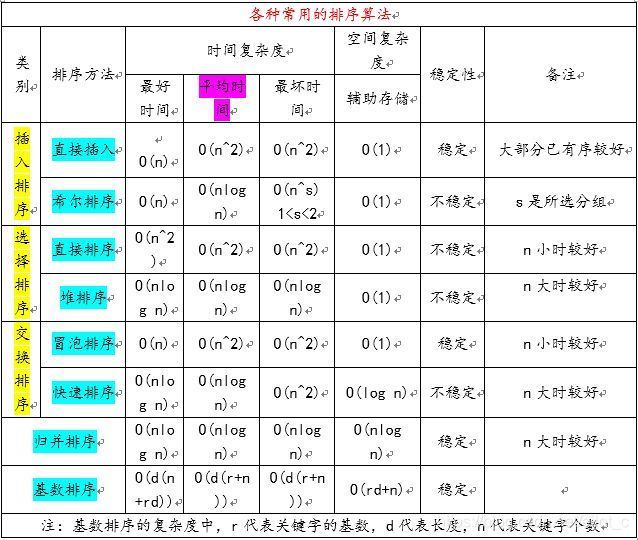
常用的几种排序算法
常用的几种排序算法
什么是算法的稳定性?
稳定性的定义:
排序前后两个相等的数相对位置不变,则算法稳定。
那么稳定有什么好处吗?
从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用
各排序算法的稳定性:
- 堆排序、快速排序、希尔排序、直接选择排序不是稳定的排序算法;
- 基数排序、冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。
1. 冒泡排序算法
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
它的时间复杂度为o(n^2)
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
![]()
def bubbleSort(arr):
for i in range(len(arr)-1):
found = False
for j in range(0,len(arr)-i-1):
if arr[j] >arr[j+1]:
arr[j],arr[j+1] = arr[j+1],arr[j]
found = True
if not found:
break
return arr
if __name__ == "__main__":
arr =[26,93,17,77,31,44,55,20,33,2,2,2,3,4,5555,6,6,6,66,67,67,76,77,3,34,34,23,232,3,3]
print(arr)
arr=bubbleSort(arr)
print(arr)
[26, 93, 17, 77, 31, 44, 55, 20, 33, 2, 2, 2, 3, 4, 5555, 6, 6, 6, 66, 67, 67, 76, 77, 3, 34, 34, 23, 232, 3, 3]
[2, 2, 2, 3, 3, 3, 3, 4, 6, 6, 6, 17, 20, 23, 26, 31, 33, 34, 34, 44, 55, 66, 67, 67, 76, 77, 77, 93, 232, 5555]
这是一种稳定的排序算法
2. 快速排序算法
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists).
它的时间复杂度为O(nlogn)
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
- 递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
![]()
def quick_sort(alist, start, end):
"""快速排序"""
if start >= end: # 递归的退出条件
return
mid = alist[start] # 设定起始的基准元素
low = start # low为序列左边在开始位置的由左向右移动的游标
high = end # high为序列右边末尾位置的由右向左移动的游标
while low < high:
# 如果low与high未重合,high(右边)指向的元素大于等于基准元素,则high向左移动
while low < high and alist[high] >= mid:
high -= 1
alist[low] = alist[high] # 走到此位置时high指向一个比基准元素小的元素,将high指向的元素放到low的位置上,此时high指向的位置空着,接下来移动low找到符合条件的元素放在此处
# 如果low与high未重合,low指向的元素比基准元素小,则low向右移动
while low < high and alist[low] < mid:
low += 1
alist[high] = alist[low] # 此时low指向一个比基准元素大的元素,将low指向的元素放到high空着的位置上,此时low指向的位置空着,之后进行下一次循环,将high找到符合条件的元素填到此处
# 退出循环后,low与high重合,此时所指位置为基准元素的正确位置,左边的元素都比基准元素小,右边的元素都比基准元素大
alist[low] = mid # 将基准元素放到该位置,
# 对基准元素左边的子序列进行快速排序
quick_sort(alist, start, low - 1) # start :0 low -1 原基准元素靠左边一位
# 对基准元素右边的子序列进行快速排序
quick_sort(alist, low + 1, end) # low+1 : 原基准元素靠右一位 end: 最后
这是一种不稳定的排序算法
举个栗子: 中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为 5 3 3 4 3 8 9 10 11, 现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱;
3. 选择排序算法
每个位置选择当前元素最小的。
它的时间复杂度为o(n^2)
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置;
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。;
![]()
def selectionsort(arr):
for i in range(len(arr)-1):
# 记录最小值的索引
minIndex = i
for j in range(i+1,len(arr)):
if arr[j] <arr[minIndex]:
minIndex = j
# i 不是最小数是,将i和最小数进行交换
if i!= minIndex:
arr[i],arr[minIndex] = arr[minIndex],arr[i]
return arr
这是一种稳定的排序算法
4. 插入排序算法
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
它的时间复杂度为o(n^2)
- 将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
- 从头到尾依次扫描未排序序列,
- 将扫描到的每个元素插入有序序列的适当位置。
- 如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。
![]()
def insertionsort(arr):
for i in range(1,len(arr)):
preIndex = i-1
current = arr[i]
while preIndex>=0 and arr[preIndex]>current:
arr[preIndex+1] =arr[preIndex]
preIndex-=1
arr[preIndex]= current
这是一种稳定的排序算法
5. 归并排序算法
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
自下而上的迭代;
它的时间复杂度为o(n^2)
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序,
- 将两个排序好的子序列合并成一个最终的排序序列。
表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间。
![]()
def mergeSort(arr):
left,right = 0, len(arr)-1
temp = [0 for _ in range(len(arr))]
return count_reverse_pairs(arr,left,right,temp)
def count_reverse_pairs(nums, left, right, temp):
if right==left: return
mid = (left+right)>>1
count_reverse_pairs(nums,left,mid,temp)
count_reverse_pairs(nums,mid+1,right,temp)
# print(left,right,mid)
if nums[mid]<nums[mid+1]: return nums
merge_and_count(nums,left,mid,right,temp)
return nums
def merge_and_count(nums, left,mid, right, temp):
"""
[left, mid] 有序,[mid + 1, right] 有序
前:[2, 3, 5, 8],后:[4, 6, 7, 12]
只在后面数组元素出列的时候,数一数前面这个数组还剩下多少个数字,
由于"前"数组和"后"数组都有序,
此时"前"数组剩下的元素个数 mid - i + 1 就是与"后"数组元素出列的这个元素构成的逆序对个数
"""
for i in range(left,right+1): temp[i] = nums[i]
i = left
j = mid+1
for k in range(left,right+1):
if i>mid:
# 说明左边结束,将右边直接赋值
nums[k] = temp[j]
j += 1
elif j>right:
# 说明右边没了,将左边赋值
nums[k] =temp[i]
i += 1
elif temp[i]> temp[j]:
# 如果左边的值比右边的大,则直接赋值
nums[k] = temp[j]
j += 1
else:
i+=1
if __name__ == '__main__':
arr = [3,44,38,5,47,15,36,26,27,3,46,4,19,50,48]
print(mergeSort(arr))
这是一种稳定的排序算法
6. 堆排序算法
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
堆排序的平均时间复杂度为 Ο(nlogn)。
- 将待排序序列构建成一个堆 H[0……n-1],根据(升序降序需求)选择大顶堆或小顶堆;
- 把堆首(最大值)和堆尾互换;
- 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
- 重复步骤 2,直到堆的尺寸为 1。
def buildMaxHeap(arr):
import math
for i in range(math.floor(len(arr)/2),-1,-1):
heapify(arr,i)
def heapify(arr, i):
left = 2*i+1
right = 2*i+2
largest = i
if left < arrLen and arr[left] > arr[largest]:
largest = left
if right < arrLen and arr[right] > arr[largest]:
largest = right
if largest != i:
swap(arr, i, largest)
heapify(arr, largest)
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def heapSort(arr):
global arrLen
arrLen = len(arr)
buildMaxHeap(arr)
for i in range(len(arr)-1,0,-1):
swap(arr,0,i)
arrLen -=1
heapify(arr, 0)
return arr
这是一种不稳定的排序算法
各排序算法的优劣
参考链接:
1
2