前面简单介绍了[ 经典的Times 33 哈希算法 ],这篇我们通过分析Java 1.8 String类的哈希算法,继续聊聊对乘数的选择。
String类的hashCode()源码
/**Cachethe hash codeforthestring*/privateinthash;/**Returnsa hash codeforthisstring.Thehash codeforaStringobjectis computedass[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]usingintarithmetic, where s[i] is the ith characterofthestring, n is the lengthofthestring,and^ indicates exponentiation. (Thehashvalueofthe emptystringis zero.) */publicinthashCode(){inth = hash;if(h ==0&&value.length >0) {charval[]=value;for(inti =0; i
可以看到,String的哈希算法也是采用了Times 33的思路,只不过乘数选择了31。
其中
hash默认值为0.
判断h == 0是为了缓存哈希值.
判断value.length > 0是因为空字符串的哈希值为0.
用数据说话
前一篇我们提到:
这个神奇的数字33,为什么用来计算哈希的效果会比其他许多常数(无论是否为质数)更有效,并没有人给过足够充分的解释。因此,Ralf S. Engelschall尝试通过自己的方法解释其原因。通过对1到256中的每个数字进行测试,发现偶数的哈希效果非常差,根据用不了。而剩下的128个奇数,除了1之外,效果都差不多。这些奇数在分布上都表现不错,对哈希表的填充覆盖大概在86%。
从哈希效果来看(Chi^2应该是指卡方分布),虽然33并不一定是最好的数值。但17、31、33、63、127和129等相对其他的奇数的一个很明显的优势是,由于这些奇数与16、32、64、128只相差1,可以通过移位(如1 << 4 = 16)和加减1来代替乘法,速度更快。
那么接下来,我们通过实验数据,来看看偶数、奇数,以及17、31、33、63、127和129等这些神奇数字的哈希效果,来验证Ralf S. Engelschall的说法。
环境准备
个人笔记本,Windows 7操作系统,酷睿i5双核64位CPU。
测试数据:CentOS Linux release 7.5.1804的/usr/share/dict/words字典文件对应的所有单词。
由于CentOS上找不到该字典文件,通过yum -y install words进行了安装。
/usr/share/dict/words共有479828个单词,该文件链接的原始文件为linux.words。
计算冲突率与哈希耗时
测试代码
/**
* 以1-256为乘数,分别计算/usr/share/dict/words所有单词的哈希冲突率、总耗时.
*
* @throws IOException
*/@TestpublicvoidtestHash()throwsIOException {List words = getWords();System.out.println();System.out.println("multiplier, conflictSize, conflictRate, timeCost, listSize, minHash, maxHash");for(inti =1; i <=256; i++) {computeConflictRate(words, i);}}/**
* 读取/usr/share/dict/words所有单词
*
* @return
* @throws IOException
*/privateList getWords()throwsIOException {// read fileInputStream is = HashConflictTester.class.getClassLoader().getResourceAsStream("linux.words");List lines = IOUtils.readLines(is,"UTF-8");returnlines;}/**
* 计算冲突率
*
* @param lines
*/privatevoidcomputeConflictRate(List lines,intmultiplier) {// compute hashlongstartTime = System.currentTimeMillis();List hashList = computeHashes(lines, multiplier);longtimeCost = System.currentTimeMillis() - startTime;// find max and min hashComparator comparator = (x,y) -> x > y ?1: (x < y ?-1:0);intmaxHash = hashList.parallelStream().max(comparator).get();intminHash = hashList.parallelStream().min(comparator).get();// hash setSet hashSet = hashList.parallelStream().collect(Collectors.toSet());intconflictSize = lines.size() - hashSet.size();floatconflictRate = conflictSize *1.0f / lines.size();System.out.println(String.format("%s, %s, %s, %s, %s, %s, %s", multiplier, conflictSize, conflictRate, timeCost, lines.size(), minHash, maxHash));}/**
* 根据乘数计算hash值
*
* @param lines
* @param multiplier
* @return
*/privateList computeHashes(List lines,intmultiplier) {Function hashFunction = x -> {inthash =0;for(inti =0; i < x.length(); i++) {hash = (multiplier * hash) + x.charAt(i);}returnhash;};returnlines.parallelStream().map(hashFunction).collect(Collectors.toList());}复制代码
执行测试方法testHash(),稍等片刻后,我们将得到一份测试报告。
哈希冲突率降序排序
通过对哈希冲突率进行降序排序,得到下面的结果。
结果分析
偶数的冲突率基本都很高,只有少数例外。
较小的乘数,冲突率也比较高,如1至20。
乘数1、2、256的分布不均匀。Java哈希值为32位int类型,取值范围为[-2147483648,2147483647]。
哈希耗时降序排序
我们再对冲突数量为1000以内的乘数进行分析,通过对执行耗时进行降序排序,得到下面的结果。
分析17、31、33、63、127和129
17在上一轮已经出局。
63执行计算耗时比较长。
31、33的冲突率分别为0.13%、0.14%,执行耗时分别为10、11,实时基本相当。
127、129的冲突率分别为0.01%、0.004%,执行耗时分别为9、10。
总体上看,129执行耗时低,冲突率也是最小的,似乎先择它更为合适?
哈希分布情况
将整个哈希空间[-2147483648,2147483647]分为128个分区,分别统计每个分区的哈希值数量,以此来观察各个乘数的分布情况。每个分区的哈希桶位为2^32 / 128 = 33554432。
之所以通过分区来统计,主要是因为单词数太多,尝试过画成图表后密密麻麻的,无法直观的观察对比。
现在加群即可获取Java工程化、高性能及分布式、高性能、高架构。性能调 优、Spring,MyBatis,Netty源码分析和大数据等多个知识点高级进阶干货 的直播免费学习权限及领取相关资料,群号:835638062 点击链接加入群聊 【Java高级架构】:https://jq.qq.com/?_wv=1027&k=5S3kL3v
计算哈希分布代码
@TestpublicvoidtestHashDistribution()throwsIOException {int[] multipliers = {2,17,31,33,63,127,73,133,237,161};List words = getWords();for(intmultiplier : multipliers) {List hashList = computeHashes(words, multiplier);Map hashMap = partition(hashList);System.out.println("\n"+ multiplier +"\n,count");hashMap.forEach((x, y) -> System.out.println(x +","+ y));}}/**
* 将整个哈希空间等分成128份,统计每个空间内的哈希值数量
*
* @param hashs
*/publicstaticMap partition(List hashs) {// step = 2^32 / 128 = 33554432finalintstep =33554432;List nums =newArrayList<>();Map statistics =newLinkedHashMap<>();intstart =0;for(longi = Integer.MIN_VALUE; i <= Integer.MAX_VALUE; i += step) {finallongmin= i;finallongmax=min+ step;intnum = (int) hashs.parallelStream().filter(x -> x >=min&& x x + y).get();asserthashNum == hashs.size();returnstatistics;}复制代码
生成数据之后,保存文本为csv后缀,通过Excel打开。再通过Excel的图表功能,选择柱状图,生成以下图表。
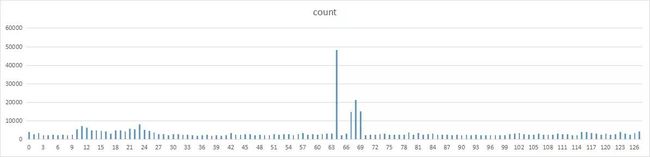
乘数2
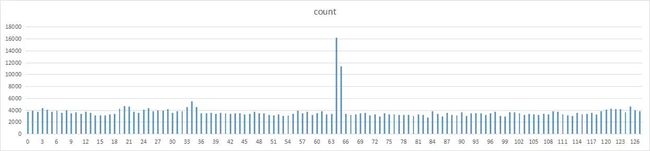
乘数17
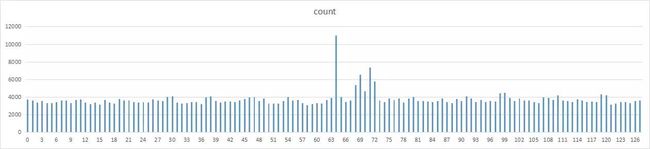
乘数31
乘数33
乘数73
乘数127
乘数133
乘数161
乘数237
除了2和17,其他数字的分布基本都比较均匀。
总结
现在我们基本了解了Java String类的哈希乘数选择31的原因了,主要有以下几点。
31是奇素数。
哈希分布较为均匀。偶数的冲突率基本都很高,只有少数例外。较小的乘数,冲突率也比较高,如1至20。
哈希计算速度快。可用移位和减法来代替乘法。现代的VM可以自动完成这种优化,如31 * i = (i << 5) - i。
31和33的计算速度和哈希分布基本一致,整体表现好,选择它们就很自然了。
当参与哈希计算的项有很多个时,越大的乘数就越有可能出现结果溢出,从而丢失信息。我想这也是原因之一吧。
尽管从测试结果来看,比31、33大的奇数整体表现有更好的选择。然而31、33不仅整体表现好,而且32的移位操作是最少的,理论上来讲计算速度应该是最快的。
最后说明一下,我通过另外两台Linux服务器进行测试对比,发现结果基本一致。但以上测试方法不是很严谨,与实际生产运行可能存在偏差,结果仅供参考。
几个常用实现选项
其中
INITIAL_VALUE:哈希初始值。Java String的初始值hash=0。
a:哈希乘数。Java String的哈希乘数为31。
参考
stackoverflow.com/questions/2…
segmentfault.com/a/119000001…
en.wikipedia.org/wiki/Univer…
《Effective Java中文版本》第2版
现在加群即可获取Java工程化、高性能及分布式、高性能、高架构。性能调 优、Spring,MyBatis,Netty源码分析和大数据等多个知识点高级进阶干货 的直播免费学习权限及领取相关资料,群号:835638062 点击链接加入群聊 【Java高级架构】:https://jq.qq.com/?_wv=1027&k=5S3kL3v