决策树

决策树

1.定义
决策树是基于树形结构进行决策的一种机器学习方法。

在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。

一般，一颗决策树包含一个根结点、若干个内部结点和若干个叶节点。叶节点对应于决策结果，其他每个节点对应于一个属性测试。每个结点包含的样本集合根据属性测试结果被划分到子节点中；根结点包含全部样本集。从根结点到每个叶结点的路径对应了一个判定测试序列。

决策树的生成是一个自顶向下的递归过程，其基本思想是以信息熵为度量构造一颗熵值下降最快的树，到叶子节点处的熵值为零。

在决策树算法中有三种情形导致递归返回：
1）当前节点包含的样本属于同一类，无需划分；
2）当前属性集为空，无法划分。此情况下，将当前结点标记为叶节点，并将其类别设定为所含样本最多的类别；利用当前结点的后验分布；（有样本无属性进行划分）
3）当前结点包含的样本集合为空，不能划分。此情况下，将当前结点标记为叶节点，将其类别设定为其父结点所含样本最多的类别；利用父结点的先验分布（无样本有属性）

2.决策树算法特点
1）决策树学习算法的最大优点是，它可以自学习。在学习过程中，不需要使用者了解过多背景知识，只需要对训练实例进行良好的标注，就能够进行学习。
2）属于有监督学习
3）从一类无序、无规则的事物（概念）中推理出决策树表示的分类规则

3.决策树学习的生成算法

关键点：如何选择最优 划分属性
目标：决策树分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”越来越高。

根据不同的目标函数，建立决策树主要有以下三种算法：

• ID3（Iterative Dichotomiser）：使用信息增益\互信息进行特征选择

取值多的属性，更容易使数据更纯，其信息增益更大。
训练得到的是一颗庞大且深度浅的树：不合理。

• C4.5：信息增益率

• CART（Classification And Regression Tree）：Gini系数

一个属性的信息增益（或信息增益率、Gini系数的降低值）越大，表明属性对样本的熵减少的能力更强，这个属性使得数据由不确定性变成确定性的能力更强。

1）信息增益

2）增益率

增益率准则对可取值数目较少的属性有所偏好。因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式，从候选划分属性中找出增益信息高于平均水平的属性，再从中选择增益率最高的。

C4.5算法继承了ID3算法的优点，并在以下几方面对ID3算法进行了改进：

1) 用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；

2) 在树构造过程中进行剪枝；

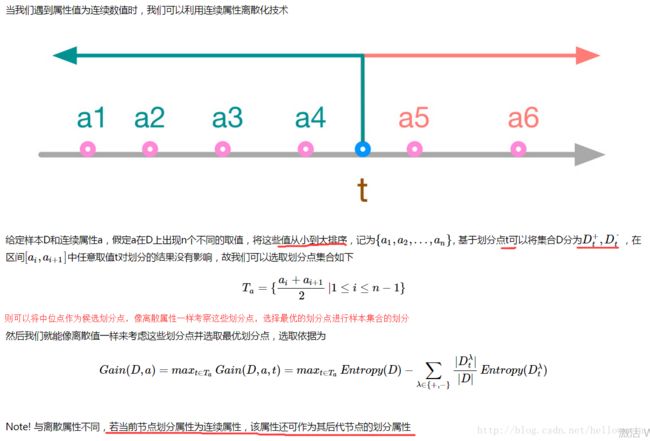
3) 能够完成对连续属性的离散化处理：以二值离散的方式处理连续型数据。

 二值离散：对连续属性值进行排序，得到多个候选阈值，选取产生最大信息增益的阈值作为分裂阈值。

连续属性离散化处理步骤：

 a）对属性的取值进行排序
 b）两个属性取值之间的中点作为可能的分裂点，将数据集分成两部分，计算每个可能的分裂点的信息增益（InforGain）
 c）对每个分裂点的信息增益(InforGain)就行修正：减去log2(N-1)/|D|
 d）选择修正后信息增益(InforGain)最大的，分裂点作为该属性的最佳分裂点
 e）计算最佳分裂点的信息增益率（Gain Ratio）作为属性的Gain Ratio
 f）选择Gain Ratio最大的属性作为分裂属性

   其中，c）、d）两点在93年Quinlan的C4.5算法中并没有体现，后来Quinlan在96年发表文章，对C4.5进行了改进，这两点是主要的修改。

   Quinlan的主要理由是数据集中同时出现连续属性和离散属性时，原始的C4.5算法倾向于选择连续的属性作为分裂属性，因此连续属性的信息增益需要减去log2(N-1)/|D|作为修正，其中N为可能的分裂点个数，|D|是数据集大小。

   第二个修改是，选择最佳分裂点不用信息增益率(Gain Ratio)，而用信息增益（Information Gain），然后用最大的信息增益对应的Gain Ratio作为属性的Gain Ratio.

4) 能够对不完整数据进行处理。

三种情况：

a）在具有缺失值的属性上如何计算信息增益率
    -忽略该类样本
    -选择常用值或均值填充
    -依据缺失比例，折算信息增益\信息增益率
    -对缺失值赋予独特的值，参与训练

b）具有缺失值的样本在进行数据分裂时，分配给哪个子数据集
    -忽略该类样本
    -选择常用值或均值填充
    -根据其他非缺失属性的比例，分配到子数据集中
    -为缺失值建立单独分支
    -确定最可能的取值，按比例仅分配给一个子数据集中

c）对新样本进行分类时，缺失值导致样本到达叶子节点，如何处理
    -有缺失值单独分支，走单独分支
    -走最常见的值的分支
    -确定最可能取值，走相应分支
    -走所有分支，根据不同输出结果进行概率组合
    -不进行分类，直接赋给最有可能的值

C4.5算法优点：产生的分类规则易于理解，准确率较高。

缺点：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。

此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

3）基尼指数

CART（Classification and Regression Tree）

4.决策树的过拟合

决策树对训练数据有很好的分类能力，但对未知测试数据未必有很好的分类能力，泛化能力弱，即可能发生过拟合现象。

• 剪枝
• 随机森林

5.剪枝策略

三种决策树的剪枝过程算法相同，区别仅是对于当前树的评价标准不同。
信息增益、信息增益率、基尼系数

1）预剪枝
定义：在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能的提升，则停止划分并并将当前结点标记为叶节点。控制决策树的生长。

a）数据划分法。将数据划分成训练样本和测试样本，使用训练样本进行训练，使用测试样本进行树生长检验。
b）阈值法。当节点的信息增益|信息增益率小于某阈值时，停止生长。
c）信息增益的统计显著性分析。统计从已有节点获得的所有信息增益|信息增益率分布，如果继续生长得到的信息增益|信息增益率与该分布相比不显著，则停止树的生长。

优点：简单、直接
缺点：对于不回溯的贪婪算法，缺乏后效性考虑，可能导致树提前停止。

2）后剪枝
定义：先从训练集生成一颗完整的决策树，然后自底向上对非叶子结点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化能力的提升，则将该子树替换为叶节点。对完全生成的决策树进行剪枝。

a）减少分类错误修剪法。使用独立的剪枝集估计剪枝前后的分类错误率，基于此进行剪枝。
b）最小代价与复杂性折中的剪枝。对剪枝后的树综合评价错误率和复杂性，决定是否剪枝。
c）最小描述长度准则。最简单的树就是最好的树，对决策树进行编码，通过剪枝得到编码最小的树。
d）规则后剪枝。将训练完的决策树转化成规则，通过删除不会降低估计精度的前件修剪每一条规则。

优点：实际应用中有效
缺点：数据量大时，计算代价较大

用留出法判断泛化性能。

6.连续值处理

7.缺失值处理

1） 删除缺失项

删除含有特征参数缺失的数据（但是如果很多数据特征参数缺失，我们会删除大量数据，一般超过三分之一的数据被删除的话不宜采用此法）

删除某个特征（如果仅仅是缺失项集中在了某几个特征，我们可以把所有数据的这些特征参数都删除，但是删除特征过多的时候不宜采用此法）

2） 猜测参数

　　我们可以根据其他项猜测缺失项可能的值。比如可以用平均值，多数法。

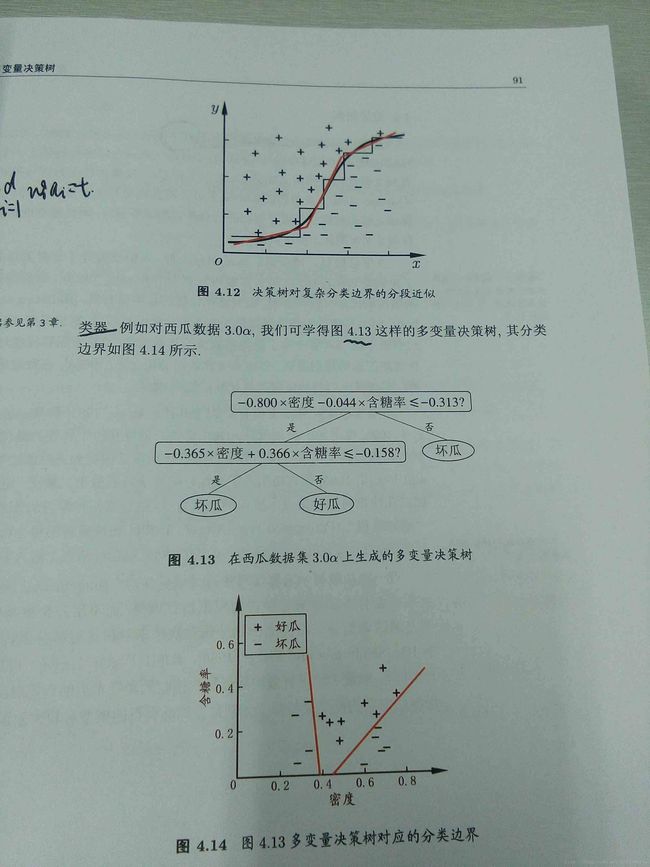
8.多变量决策树
n个变量——n维空间
与传统的“单变量决策树”不同，在多变量决策树学习过程中，不是为每个非叶结点寻找一个 最优划分属性，而是试图建立一个合适的分类器。