强网杯-JustRe

Windows32位程序，无壳，编译器版本还算高。

主函数除了CFG有点诡异外，流程十分简单。

进入第一个check函数，可以看到大量SSE指令，前面一些基本的判断很不好看，直接调试看结果

.text:00401682 060                 movd    xmm0, eax
.text:00401686 060                 pshufd  xmm5, xmm0, 0
.text:0040168B 060                 test    ecx, ecx
.text:0040168D 060                 jz      loc_401

到达以上基本块时可以发现，第一行eax的结果是string2hex(input[0:8])，刚好32字节，这说明我们的输入必须为十六进制字符。之后可以看到一堆复杂的运算，且都是通过xmm寄存器来实现的

 

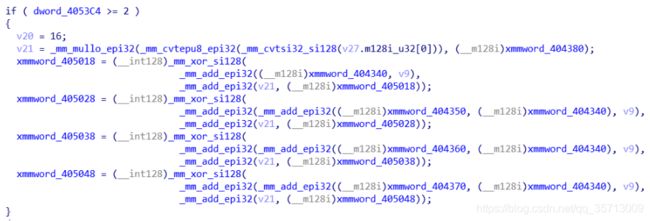
这里操作的变量均为128位，v21是input[8:10]两个字符一直重复8次的hex值，而v9则是之前所说的前8个字符的hex值。最终运算的结果会与一个函数的数据进行比较，如果完全匹配则将这些数据写入到另一个函数中，如下

也就是说，这里可以通过类似解方程的方式来求出v9和v21，这样就能得到前10字节的输入

虽然这里还有以上一个约束条件，不过由于v9和v21的十六进制形式有特定的重复模式，所以可以不用这个。最终可以通过模拟SSE指令的运算，然后使用z3来约束求解，求出前10字节。模拟这个运算还是挺麻烦的，应该还有更轻松的解法。脚本如下

from z3 import *

flag = ''

def xmm2dwords(value):
    temp = []
    for i in range(4):
        temp.append(value >> (i*32))
    return temp

def dwords2xmm(dwords):
    ret = 0
    for i in range(4):
        ret += dwords[i] << (i*32)
    return ret

def xmm_add32(a, b):
    for i in range(4):
        a[i] += b[i]
        a[i] &= 0xffffffff
    return a

def xmm_xor(a, b):
    for i in range(4):
        a[i] ^= b[i]

def xmm_caculate(key, value):
    global v9, v21
    keys = xmm2dwords(key)
    values = xmm2dwords(value)
    temp9 = xmm2dwords(v9)
    temp21 = xmm2dwords(v21)
    xmm_add32(keys, temp9)
    xmm_add32(temp21, values)
    xmm_xor(temp21, keys)
    return dwords2xmm(temp21)

key = [0x3000000020000000100000000, 0x4000000040000000400000004, 0x8000000080000000800000008, 0x0C0000000C0000000C0000000C]

xmm_data = [0x3E5F11D5FE0F0B1DEA90BD987BB39408, 0x3E507535EE160D39FC3AF1B485CAFC37,
            0x5816BBEF29EB512E075D0CFC3DCF6D3B, 0x64194E32074EF0FDB0162F403E50853C]
xmm_func = [0x405004a100000278ec81f0e483ec8b55, 0x4041a805100f00000274248489c43300,
            0x7e0ff3572c2444110f56004041c0a000, 0x6a0a41100f402444d60f66004041b805]

v21 = BitVec('v21', 16*8)
v9 = BitVec('v9', 16*8)

solver = Solver()
solver.add(xmm_func[0] == xmm_caculate(key[0], xmm_data[0]))
solver.add(xmm_func[1] == xmm_caculate(dwords2xmm(xmm_add32(xmm2dwords(key[1]), xmm2dwords(key[0]))), xmm_data[1]))
solver.add(xmm_func[2] == xmm_caculate(dwords2xmm(xmm_add32(xmm2dwords(key[2]), xmm2dwords(key[0]))), xmm_data[2]))
solver.add(xmm_func[3] == xmm_caculate(dwords2xmm(xmm_add32(xmm2dwords(key[3]), xmm2dwords(key[0]))), xmm_data[3]))
solver.add(v9&0xffffffff == (v9 >> 32)&0xffffffff)
solver.add(v9&0xffffffff == (v9 >> 32*2)&0xffffffff)
solver.add(v9&0xffffffff == (v9 >> 32*3)&0xffffffff)

temp = v21
for i in range(15):
    solver.add(temp&0xff == (temp>>8)&0xff)
    temp >>= 8
print solver.check()
m = solver.model()
print hex(int(str(m[v9])))[2:8+2] + hex(int(str(m[v21])))[2:2+2]

接着我们来分析覆盖后的函数，可以用IDC脚本直接将正确的函数数据patch到目标函数中，然后来分析。可以看到该函数连续调用了0x401000这个函数3次，进去看了后很复杂，估计是某种加密方式，用插件看一眼是DES

 

而前面又存在明文，并分3次写入缓冲区

那么可以确定0x401000函数就是密钥扩展了，前面的明文就是3个密钥了，而这里进行了3次密钥扩展，可以想到三重DES.

密钥扩展结束后就是加密过程了，稍微跟踪下就会发现这个过程是在0x401500函数进行的，跟进之后先对输入进行漂白，然后调用3次0x401250函数，然后漂回去。那么0x401250就是加密函数了。但这里有个小坑

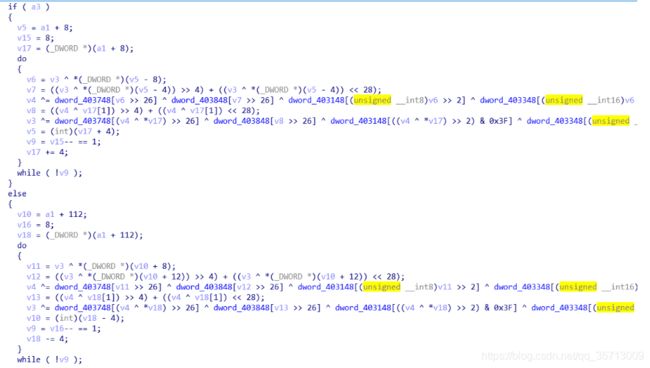
第3个参数用来决定是DES加密还是解密，1表示加密，0表示解密。我们知道DES的加密解密过程是相同的，只是扩展的子密钥是相反的

可以看到参数3为1时在这里子密钥每次增加4个dword即48位，为0时则是减少48位，由此可看出加密和解密的模式。

了解了这些就可以直接对最后的密文解密了，脚本如下

from Crypto.Cipher import DES
s = '\x50\x7C\xA9\xE6\x87\x09\xCE\xFA\x20\xD5\x0D\xCF\x90\xBB\x97\x6C'
des0 = DES.new('AFSAFCED', DES.MODE_ECB)
des1 = DES.new('YCXCXACN', DES.MODE_ECB)
des2 = DES.new('DFKDCQXC', DES.MODE_ECB)
text = des0.decrypt(des1.encrypt(des2.decrypt(s)))
print text