强化学习策略梯度梳理1 - REINFORCE（附代码）

主要参考文献 Reinforcement Learning: An introduction，Sutton
主要参考课程 Intro to Reinforcement Learning，Bolei Zhou
相关文中代码 https://github.com/ThousandOfWind/RL-basic-alg.git

策略梯度（PG）

首先定义遵从一般约定
$s\in \mathcal{S},a\in \mathcal{A}(s),\mathbf{\theta }\in {\mathbb{R}}^{d^{\prime }}$

既然策略是 $\pi (a\mid s,\mathbf{\theta })=\mathrm{Pr}\left\{A_t=a\mid S_t=s,{\mathbf{\theta }}_t=\mathbf{\theta }\right\}$
我们假设这个策略有表现$J\left(\mathbf{\theta }\right)$
我们希望能够根据$J$的梯度更新策略 ${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t+\alpha \nabla J\left({\mathbf{\theta }}_t\right)$

方向导数本质上研究的是函数在某点处沿某特定方向上的变化率问题，梯度反映的是空间变量变化趋势的最大值和方向。方向导数与梯度在微分学中有重要的运用。
具体等我把相关算法搞定再去看高数

这样问题就变成了怎么把表现和策略联合起来
然后sutton就说了，既然如此
$J(\mathbf{\theta })\doteq v_{{\pi }_{\mathbf{\theta }}}\left(s_0\right)$
$v_{\pi }(s)=\left[{\sum }_a\pi (a\mid s)q_{\pi }(s,a)\right]$
⚠️用状态$s_0$的价值是因为他还假设了条件$\gamma =1$，所以$v_{{\pi }_{\mathbf{\theta }}}\left(s_0\right)$ 实际上能够代表轨迹上的收益和
因此$J$的梯度可以参考状态值的梯度

$$\begin{array}{rl}\nabla v_{\pi }(s)& =\nabla \left[\sum _a\pi (a\mid s)q_{\pi }(s,a)\right],\text{ for all }s\in \mathcal{S}\\ & =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\nabla q_{\pi }(s,a)\right]\\ & =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\nabla \sum _{s^{\prime },r}p\left(s^{\prime },r\mid s,a\right)\left(r+v_{\pi }\left(s^{\prime }\right)\right)\right]\\ & =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\nabla \sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)v_{\pi }\left(s^{\prime }\right)\right]\\ & =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\nabla \sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)\left(\sum _{a^{\prime }}\left[\nabla \pi (a^{\prime }\mid s^{\prime })q_{\pi }(s^{\prime },a^{\prime })+\pi (a^{\prime }\mid s^{\prime })\nabla \sum _{s^{\prime \prime }}p\left(s^{\prime \prime }\mid s^{\prime },a^{\prime }\right)v_{\pi }\left(s^{\prime \prime }\right)\right]\right)\right]\end{array}$$

然后接下这一步其实我没懂。。罪过。我看完这个立刻去学

$$=\sum _{x\in \mathcal{S}}\sum _{k=0}^{\infty }\mathrm{Pr}(s\to x,k,\pi )\sum _a\nabla \pi (a\mid x)q_{\pi }(x,a)$$

anyway，
$$J(\mathbf{\theta })\propto \sum _s\mu (s)\sum _a{q}_{\pi }(s,a)\nabla \pi (a\mid s,\mathbf{\theta })$$
符号$\propto$ 是“正比于”的意思，就很合理，策略梯度也因此有很好的收敛性保证

进一步，我们可以推

$$\begin{array}{rl}\sum _s\mu (s)\sum _a{q}_{\pi }(s,a)\nabla \pi (a\mid s,\mathbf{\theta })& ={\mathbb{E}}_{\pi }\left[\sum _a{q}_{\pi }\left(S_t,a\right)\nabla \pi \left(a\mid S_t,\mathbf{\theta }\right)\right]\\ & ={\mathbb{E}}_{\pi }\left[\sum _a\pi (a\mid S_t,\mathbf{\theta })q_{\pi }(S_t,a)\frac{\nabla \pi (a\mid S_t,\mathbf{\theta })}{\pi (a\mid S_t,\mathbf{\theta })}\right]\\ & ={\mathbb{E}}_{\pi }\left[q_{\pi }(S_t,A_t)\nabla \ln (\pi (A_t\mid S_t,\mathbf{\theta }))\right]\end{array}$$

所以虽然J值是我们用来评估策略表现的，但是很多时候，我们说$\ln (\pi (a\mid s,\mathbf{\theta }))$是score function
(我怀疑我又在胡说八道了。。。。

REINFORCE

如果用真实奖赏估计$v_{\pi }(s)$，我们就得到了这个算法
他的核心思路是用MC方法估计$q_{\pi }(S_t,A_t)$项
也就是说
$$J(\mathbf{\theta })\propto {\mathbb{E}}_{\pi }\left[G(S_t,A_t)\nabla \ln (\pi (A_t\mid S_t,\mathbf{\theta }))\right]$$

突然意识到两年了我都没写过MC的代码，然后决定试试看

首先就是教科书里的伪代码

然后python实现是这个样

    def get_action(self, observation, *arg):
        obs = th.FloatTensor(observation)
        pi = self.pi(obs=obs)
        m = Categorical(pi)
        action_index = m.sample()

        self.log_pi_batch.append((m.log_prob(action_index)))
        return int(action_index), pi

    def learn(self, memory):
        batch = memory.get_last_trajectory()

        # build G_t
        G = copy.deepcopy(batch['reward'][0])
        for index in range(2, len(G)+1):
            G[-index] += self.gamma * G[-index + 1]
        G = th.FloatTensor(G)

        log_pi = th.stack(self.log_pi_batch)
        J = - (G * log_pi).mean()

        self.writer.add_scalar('Loss/J', J.item(), self._episode )
        self.optimiser.zero_grad()
        J.backward()
        grad_norm = th.nn.utils.clip_grad_norm_(self.params, 10)
        self.optimiser.step()

        self._episode += 1

但是但是，
我先试了一下小车爬坡效果很不行，参考了周老师的tutorial里推荐的源码： https://github.com/cuhkrlcourse/RLexample/blob/master/ policygradient/reinforce.py
用的环境是’CartPole-v1’，然而效果还是很糟糕。。。
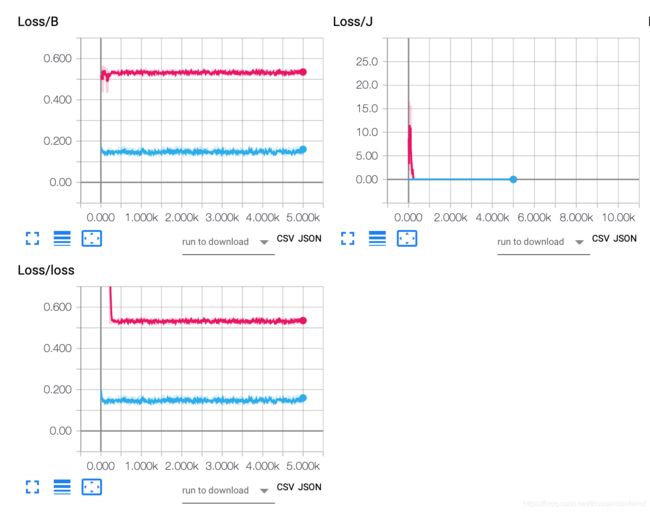
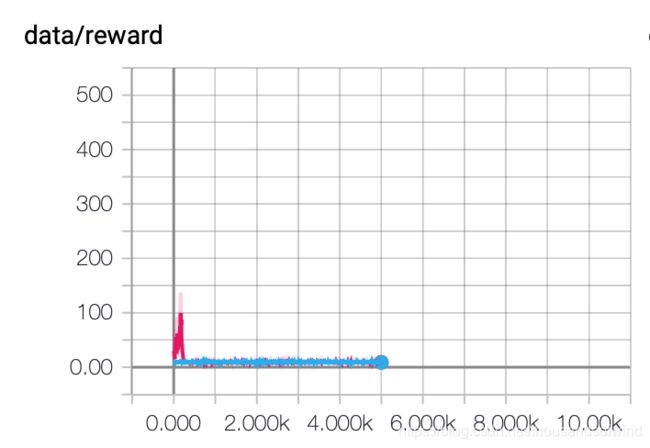
这里贴贴一下结果
loss & score虽然说收敛了但是解很不好， 是我哪里写错了吗。。。

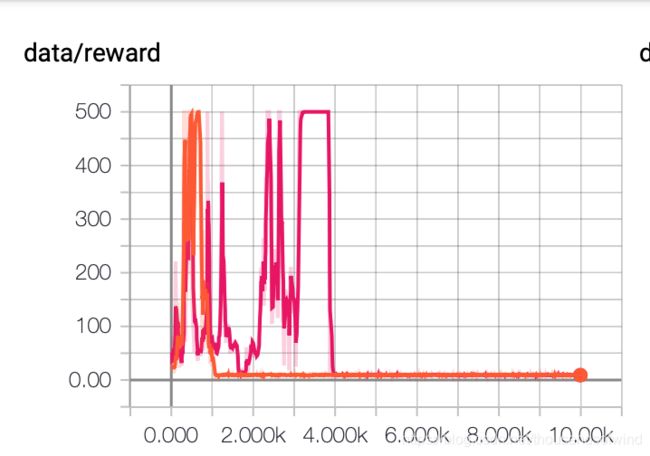
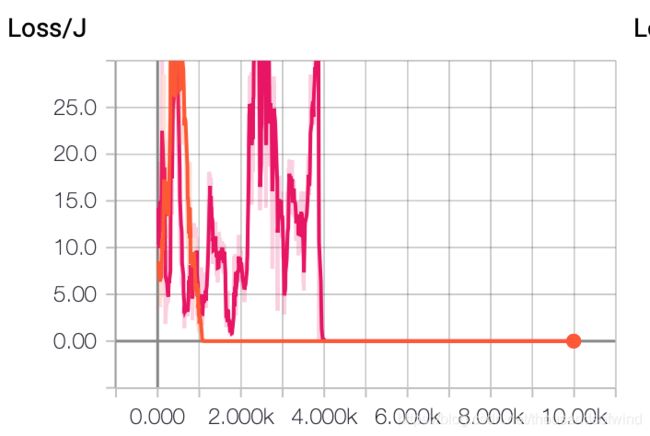
然后可视化了他的行动策略，红色和绿色分别是一个动作
，这样看的话它只有在做一个动作而已

REINFORCE-baseline

因为上文用的是
$$\nabla J(\mathbf{\theta })\propto {\mathbb{E}}_{\pi }\left[G(S_t,A_t)\nabla \ln (\pi (A_t\mid S_t,\mathbf{\theta }))\right]$$
baseline的使用是因为$G(S_t,A_t)$的会带来很高的方差， 为了缓解这个问题我们考虑存在一个baseline 满足
$$\sum _{a}b(s)\nabla \pi (a\mid s,\mathbf{\theta })=b(s)\nabla \sum _a\pi (a\mid s,\mathbf{\theta })=b(s)\nabla 1=0$$
这样
$$\nabla J(\mathbf{\theta })\propto \sum _s\mu (s)\sum _a\left(q_{\pi }(s,a)-b(s)\right)\nabla \pi (a\mid s,\mathbf{\theta })$$
然后一般会用状态值作为baseline

    def get_action(self, observation, *arg):
        obs = th.FloatTensor(observation)
        pi = self.pi(obs=obs)
        m = Categorical(pi)
        action_index = m.sample()

        self.log_pi_batch.append(m.log_prob(action_index))
        self.b_batch.append(self.B(obs=obs))
        return int(action_index), pi

    def learn(self, memory):
        batch = memory.get_last_trajectory()

        # build G_t
        G = copy.deepcopy(batch['reward'][0])
        reward = th.FloatTensor(batch['reward'][0])

        for index in range(2, len(G) + 1):
            G[-index] += self.gamma * G[-index + 1]
        G = th.FloatTensor(G)


        log_pi = th.stack(self.log_pi_batch)
        b = th.stack(self.b_batch)
        J = - ((G-b).detach() * log_pi).mean()
        value_loss = F.smooth_l1_loss(b.squeeze(-1), reward).mean()

        loss = J + value_loss

        self.writer.add_scalar('Loss/J', J.item(), self._episode)
        self.writer.add_scalar('Loss/B', value_loss.item(), self._episode)
        self.writer.add_scalar('Loss/loss', loss.item(), self._episode)


        self.optimiser.zero_grad()
        loss.backward()
        grad_norm = th.nn.utils.clip_grad_norm_(self.params, 10)
        self.optimiser.step()

        self._episode += 1

然而结果也很悲剧

对比DQN

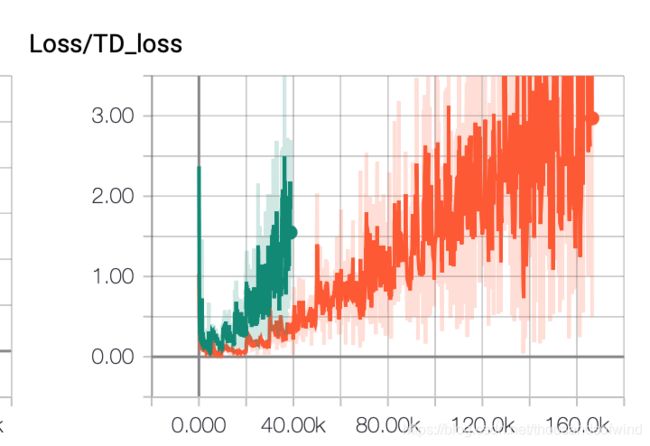
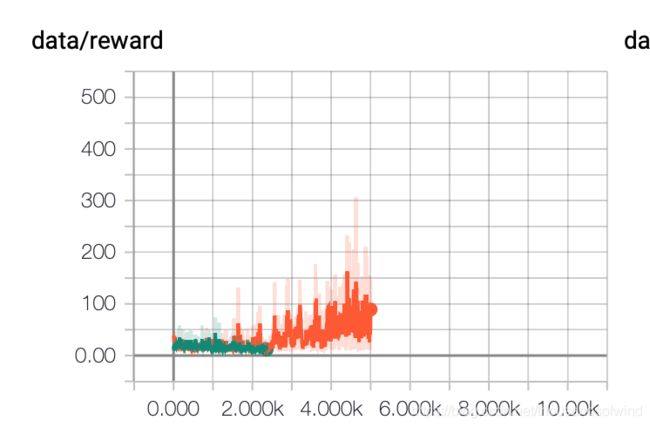
因为我很怀疑是不是我的代码有什么问题就决定对比一下dqn，虽然dqn发散，但是效果果然好很多，而且策略的颜色也是比较理想的那种

总结

onpolicy 果然收敛的很好然而效果不好
offpolicy 虽然不收敛但是又能看到效果
然而两个结果都很糟糕，
可能原因包括

• 可能我的参数不好
• 网络结构不够好，一般经验来看可能换rnn会好一些
• 我写的代码有问题。。。。等我找到原因会回来改改的