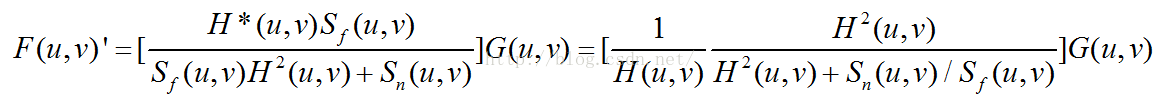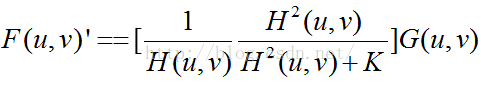维纳滤波在图像复原中的应用

      图像退化/复原模型

     g(x,y) = h(x,y)*f(x,y)+n(x,y)     频域：G(u,v) = H(u,v)F(u,v) +N(u,v)

     其中f(x,y)为原始图像，h(x,y)为退化函数，n(x,y)为噪声函数，目标就是根据观测图像g(x,y)以及一些先验或者估计信息复原f(x,y)

     图像复原的核心内容就是估计退化函数，因为当噪声N为0时，F = G/H，知道了退化函数，即可复原原图像，但是当N不为0时，且H较小时，无法直接使用盲复原（噪声被过度放大）。

     维纳滤波

      维纳滤波又叫最小均方差滤波，它的目标是找到一个原图像f的估计图像f'，使得它们之间的均方误差最小。

      数学表达式：  e^2 = E(（f-f'）^2)

   

      根据假设，推导出估计图像的表达式如下：

      

        从上公式可以看到，该表达式将估计图像和原图像的信噪比相联系，当H(u,v)和信噪比（Sf/Sn）较大时，该公式接近盲复原公式G/H，当信噪比较小时，会对该区域复原图像除以一个大于1的系数（压制作用）。

      当处理白噪声时，噪声功率谱Sn是一个常数，大大简化处理。然而未退化功率谱很少是已知的，一般用下式表示，K是一个特定常数，用来找到最好视觉效果。

    

         维纳滤波是图像复原中常用的一种复原方法，常与其他方法共同使用完成图像复原。此外，盲去卷积算法在图像复原中也有着重要的意义，可参考：盲去卷积在图像复原中的作用，相比维纳来讲，它不需要如此多的先验知识。

     维纳滤波MATLAB实验

     MATLAB关于维纳滤波函数有wiener2和deconvwnr，分别适用于灰度图像和彩色图像，这里只使用wiener2

     实验代码：

     I=imread('lena.jpg');

     noise=5*randn(size(I));
     noise = noise - min(min(noise));

     J  = double(I) +noise;      

     R1=wiener2(J,[10 10]);    %未知噪声

     R2=wiener2(J,[10 10],noise);  %已知噪声分布

     figure
     subplot(2,2,1),imshow(uint8(I));title('原始图像');
     subplot(2,2,2),imshow(uint8(I1));title('退化图像');
     subplot(2,2,3),imshow(uint8(R1));title('盲复原');

     subplot(2,2,4),imshow(uint8(R2));title('非盲复原');

     实验结果