下一个排列

C++有一个 库 algorithm (算法)，里面有关于下一个排列，前一个排列的函数，分别是 next_permutation()、prev_permutation。

• next_permutation()：求一个排序的下一个排列的函数，可以遍历全排列
• prev_permutation：求一个排序的上一个排列的函数

---

 

输入一组数列，下一个排列情况如下：

输入1,2,3，即返回下一组排列刚好大于1,2,3的下一个排列，如果输入的，如3,2,1，已经是最大值，即返回最小值排列。 

1. 1,2,3 -> 1,3,2
2. 1,3,2 -> 2,1,3
3. 2,1,3 -> 2,3,1
4. 2,3,1 -> 3,1,2
5. 3,1,2 -> 3,2,1
6. 3,2,1 -> 1,2,3

首先，这里需要先观察规律，可以多列几组数据，考究一下自身查找思考找到下一个最小值的过程。

1. 是否有边界问题（也就是鲁棒性）
2. 分解自身思考的过程，从前向后找，从后往前找。确定最大数，确定最小数。采取什么的方式确定最小值，思考。

---

 分析：

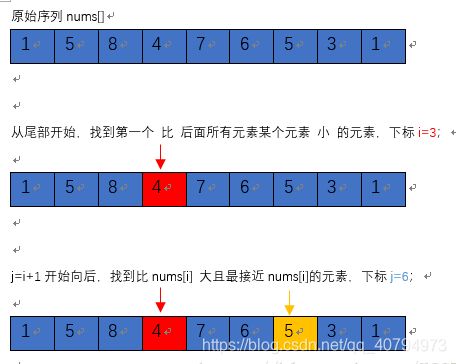
假设此时给出的状态时5 2 4 3 1，那么下一个状态要如何确定呢？首先从人的视角来看，绝对会从序列末尾向前开始查找，例如如果给的状态时1 2 3 4 5，则很容易发现下一个状态应该是1 2 3 5 4，这样就给出了一个策略，第一步应该先找从末尾开始向前第一对非逆序数对，这当然有理由，因为如果是逆序的，说明该种情况一定是已经进行过交换了，则绝对不会是下一种情况交换的候选位置，因此会发现5 2 4 3 1中第一个非逆序数对是2 4，所以交换的候选对象应该是2（2是较小的那一个）；紧接着继续思考，应该和后面的哪一个进行交换。首先显而易见的是，2后面的子序列一定是逆序的。那么如果要和2交换并且使结果是字典序的下一个的话，那么与2交换的一定是2后面的比2大的最小的哪一个数，因此第二步就是从序列末尾开始向前查找第一个比2大的数，与2进行交换（此时为 5 3 4 2 1），那么下一步也是显而易见的，3后面的序列应该是由5 3开始的字典序最小的一个序列，因此要将3后面的序列逆置。最后得到答案5 3 1 2 4。

注：在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。 一个排列中逆序的总数就称为这个排列的逆序数。

图解：

第一种解法的思路：

输入初始排序的数组{
       1.如果数组长度为1或者为0
              直接返回数组
       2.如果数组长度为2
              直接交换数组中两个值的位置
              返回交换后的数组
       3.从最后一个值开始向前查找（循环1）
                 如果[这个值]比[前一个值]大（判断）
                        从最后往前查找截止到[这个值]（循环2）
                                   如果出现有值大于[前一个值]（判断）
                                           交换这两个值的位置
                                           跳出循环2
                        遍历这个值的后一个值到末位（循环）
                                数字从两边分别交换数值，一直到中间
                        返回数组
       4.排除前面三种情况，说明排序已经是从前往后是最大值（由最大变为最小）
          遍历从前到中间的位置(循环)
                 数字从两边分别交换数值，一直到中间
          返回数组
}

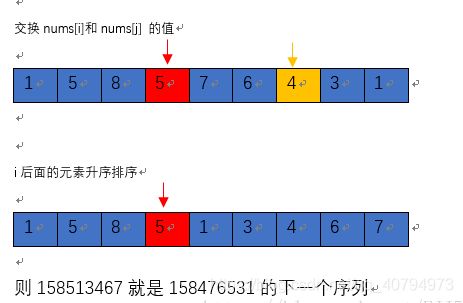
这里最难想象的情况是第三种，我们以 1,3,5,8,4,7,6,5,3,1 这串数字来例子说明，1,3,5,8,4,7,6,5,3,1->1,3,5,8,5,7,6,4,3,1 从后往向前找，找到后数比前数大的情况，找到4比7小，这个确认值就为4，再重新从最后往前找，有第一个数（5）出现比这个确认值（4）大的情况，将这两个值交换。

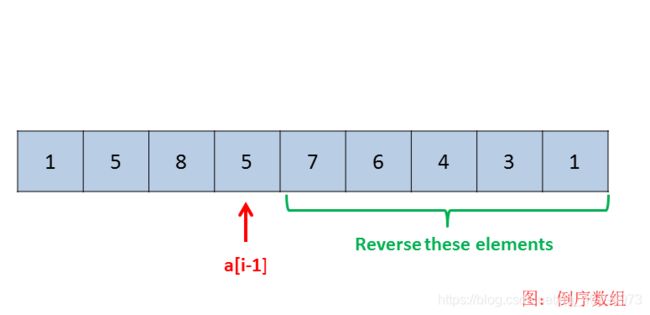
 1,3,5,8,5,7,6,4,3,1->1,3,5,8,5,1,3,4,6,7 然后把7,6,4,3,1倒序之后，就是下一个排列了

输入初始排序的数组
vector nextPermutation(vector &nums) {
   1.如果数组长度为1或者为0
    if(nums.size() == 1 || nums.size() == 0)
        直接返回数组
        return nums;
    2.如果数组长度为2
    if(nums.size() == 2) {
        直接交换数组中两个值的位置
        swap(nums[0], nums[1]);
        返回交换后的数组
        return nums;
    }
    3.从最后一个值开始向前查找（循环1）
    for(int i = nums.size() - 1; i > 0; i--) {
        如果[这个值]比[前一个值]大（判断）
        if(nums[i] > nums[i - 1]) {
            从最后往前查找截止到[这个值]（循环2） 
            for(int j = nums.size() - 1; j >= i; j--)
                如果出现有值大于[前一个值]（判断）
                if(nums[j] > nums[i - 1]) {
                    交换这两个值的位置
                    swap(nums[i - 1], nums[j]);
                    跳出循环2
                    break;
                }
            遍历这个值的后一个值到末位（循环）
            for(int j = 0; j < (nums.size() - i) / 2; j++)
                数字从两边分别交换数值，一直到中间
                swap(nums[i + j], nums[nums.size() - j - 1]);
            return nums;
        }
    }
    4.排除前面三种情况，说明排序已经是最大值
    遍历从前到中间的位置(循环)
    for(int j = 0; j < nums.size() / 2; j++)
        数字从两边分别交换数值，一直到中间
        swap(nums[j], nums[nums.size() - j - 1]);
    返回数组
    return nums;
}

 时间复杂度O(N平方)，空间复杂度是O(1)

是否有更优的解法呢？

第二种解法：时间O(N) 空间O(1)
关键在于将第三个阶段分解，将两个循环拆分，即可减少时间复杂度。

1. 从后往向前找，找到后数比前数大的情况，记住这个值，结束循环
2. 从最后往前找，在第一个出现比这个值大的情况，交换这两个值交换。
3. 将这个值之后的数组倒序排列，就是下一个排列了

public void nextPermutation(vector& nums) {
        i为数组倒数第二个值，j为倒数第一个值
        int n = nums.size(), i = n - 2, j = n - 1;
        找出倒数第二个值比倒数第一个值要小的时候，此时找到确认值（循环）
        while (i >= 0 && nums[i] >= nums[i + 1]) 
        下一个数
              --i;
        如果找到最后能找到需要交换的值
        if (i >= 0) {
           循环查找到确认值之后第一个大于确认值的的数（循环）
            while (nums[j] <= nums[i]) 
            --j;
            交换确认值和这个数的位置
            swap(nums[i], nums[j]);
        }
        倒序确认值之后的数组
        reverse(nums.begin() + i + 1, nums.end());
    }

可以看到没有循环叠加所以时间复杂度是O(n),时间复杂度为O(1)

public void reverse(int []nums,int l,int r){
        while(l=1;i--){
            if(nums[i]>nums[i-1])
                break;
        }
        if(i==0){
            Arrays.sort(nums);
            return;
        }
        int index=i-1;
        int diff=nums[i-1];
        for(i=nums.length-1;i>=0;i--){
            if(nums[i]>diff)
                break;
        }
        int tmp=nums[index];
        nums[index]=nums[i];
        nums[i]=tmp;
        reverse(nums,index+1,nums.length-1);
    }

java实现第一种方法：

/**
 * 1,3,5,8,4,7,6,5,3,1->1,3,5,8,5,7,6,4,3,1  --交换4和5-->  1,3,5,8,5,7,6,4,3,1 --7,6,4,3,1倒序-> 1,3,5,8,5,1,3,4,6,7
 */
@Test
public void test() {
    ArrayList arr = new ArrayList<>();
    arr.add(1);
    arr.add(3);
    arr.add(5);
    arr.add(8);
    arr.add(4);
    arr.add(7);
    arr.add(6);
    arr.add(5);
    arr.add(3);
    arr.add(1);
    ArrayList change = nextPermutation(arr);
    System.out.println(change);

}

/**
 * @param arr 输入初始排序的数组
 * @return
 */
public static ArrayList nextPermutation(ArrayList arr) {
    //1.如果数组长度为1或者为0
    if (arr.size() == 1 || arr.size() == 0) {
        //直接返回数组
        return arr;
    }
    //2.如果数组长度为2
    if (arr.size() == 2) {
        //直接交换数组中两个值的位置  swap(nums[0], nums[1]);
        int t = arr.get(0);
        arr.set(0, arr.get(1));
        arr.set(1, t);
        //返回交换后的数组
        return arr;
    }
    //3.从最后一个值开始向前查找（循环1）
    for (int i = arr.size() - 1; i > 0; i--) {
        //如果[这个值]比[前一个值]大（判断）  1,3,5,8,4,7,6,5,3,1->1,3,5,8,5,7,6,4,3,1  --交换4和5-->  1,3,5,8,5,7,6,4,3,1 --7,6,4,3,1倒序-> 1,3,5,8,5,1,3,4,6,7
        if (arr.get(i) > arr.get(i - 1)) {//这个值下标是 i-1  上面样例中的7
            //从最后往前查找截止到[这个值]（循环2）
            for (int j = arr.size() - 1; j >= i; j--) {
                //如果出现有值大于[前一个值]（判断 i - 1）
                if (arr.get(j) > arr.get(i - 1)) {//找到了 5 > 4  1,3,5,8,4,7,6,5,3,1->1,3,5,8,5,7,6,4,3,1  --交换4和5-->  1,3,5,8,5,7,6,4,3,1
                    //交换这两个值的位置   swap(nums[i - 1], nums[j]);   1,3,5,8,(4),7,6,(5),3,1
                    int t = arr.get(i - 1);
                    arr.set(i - 1, arr.get(j));
                    arr.set(j, t);
                    //跳出循环2
                    break;
                }
            }
            //遍历这个值的后一个值到末位（循环） 7,6,4,3,1  倒序 1,3,5,8,5,7,6,4,3,1 --7,6,4,3,1倒序-> 1,3,5,8,5,1,3,4,6,7
            for (int j = 0; j < (arr.size() - i) / 2; j++) {//现在 i 的下标指向的是 7,6,4,3,1 的 7  (10-6)/2 = 2  就是找一半
                // 数字从两边分别交换数值，一直到中间
                // swap(nums[i + j], nums[nums.size() - j - 1]);
                int t = arr.get(i + j);
                arr.set(i + j, arr.get(arr.size() - j - 1));
                arr.set(arr.size() - j - 1, t);
            }
            return arr;
        }
    }
    //4.排除前面三种情况，说明排序已经是最大值(这个时候已经是最大的了，只需要全部倒叙就成了最小的了)
    // 遍历从前到中间的位置(循环)
    for (int j = 0; j < arr.size() / 2; j++) {
        // 数字从两边分别交换数值，一直到中间
        // swap(nums[j], nums[nums.size() - j - 1]);
        int t = arr.get(j);
        arr.set(j, arr.get(arr.size() - j - 1));
        arr.set(arr.size() - j - 1, t);
    }
    //返回数组
    return arr;
}

---

洛谷：https://www.luogu.org/problemnew/show/P1088

这道题没有上面那么多条件，下一个排序一定是存在的，不会超过最大值。

c++函数解决

#include
#include
using namespace std;
int a[10005], n, m;
int main() {
	scanf("%d%d", &n, &m);
	for (int i = 0; i < n; i++) {
		scanf("%d", &a[i]);
	}
	while (m--) {
		next_permutation(a, a + n);
	}
	for (int i = 0; i < n - 1; i++) {
		printf("%d ", a[i]);
	}
	printf("%d", a[n - 1]);//不能有多余的空格,单独输出
	return 0;
}

java

import java.io.*;
import java.util.Arrays;
/**
 * 把火星人用手指表示的数与科学家告诉你的数相加，并根据相加的结果改变火星人手指的排列顺序
 * 输入数据保证这个结果不会超出火星人手指能表示的范围
 */
public class Main {
    private static int[] arr;
    private static int n;//火星人手指的数目

    public static void main(String[] args) throws IOException {
        StreamTokenizer input = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        int m;//要加上去的小整数
        input.nextToken();
        n = (int) input.nval;
        input.nextToken();
        m = (int) input.nval;
        arr = new int[n];
        for (int i = 0; i < n; i++) {
            input.nextToken();
            arr[i] = (int) input.nval;
        }
        for (int i = 0; i < m; i++) {
            nextPermutation();
        }

        Arrays.stream(arr)
                .forEach((x)->{System.out.print(x+" ");});

    }


    /**
     * 获取下一个排列
     */
    public static void nextPermutation() {
        if (n == 1) {
            return;
        }
        //swap(nums[0], nums[1]);
        if (n == 2) {
            int t = arr[0];
            arr[0] = arr[1];
            arr[1] = t;
            return;
        }

        //i为数组倒数第二个值，j为倒数第一个值
        int i = n - 1;
        while (i >= 1 && arr[i] < arr[i - 1]) { //1,3,5,8,(4),7,6,(5),3,1->1,3,5,8,5,7,6,4,3,1
            --i;
        }
        int j = n - 1;
        --i;//取前面那个小的数
        while (arr[i] > arr[j]) {//重后往前找，找到第一个比这个数大的 下标
            --j;
        }

        //交换 i j
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;

        //i + 1 ~ n -1 逆序
        reverse(i + 1, n - 1);
    }

    private static void reverse(int i, int j) {
        int temp;
        while (i <= j) {
            temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++;
            j--;
        }
    }
}

LeetCode的Next Permutation：https://leetcode.com/problems/next-permutation/description/

---

参考：https://blog.csdn.net/chaoweilanmaohhh/article/details/79690453     https://blog.csdn.net/FJJ543/article/details/82151010

 https://www.jianshu.com/p/0fb544271bb5