改进粒子滤波算计及其matlab实现

Github个人博客：https://joeyos.github.io

基本粒子滤波存在的问题

基本粒子滤波算法中普遍存在的问题是退化现象，这是因为粒子权值的方差会随着时间的迭代而不断增加。退化现象是不可避免的，经过若干次迭代，除了少数粒子外，其他粒子的权值可以忽略不计。退化的意味着如果继续跌代下去，那么大量的计算资源就会消耗在处理那些微不足道的粒子上。可以采取如下措施避免：

（1）增加粒子数
增加粒子数也叫增加采样点，粒子数目多，自然能全面反映粒子多样性，能延缓退化，但运算量增大。

（2）重采样的本质是增加粒子的多样性。SIR粒子滤波在这点上做得比SIS粒子滤波成功。引入重采样机制，基本上避免了粒子丧失多样性的可能。重采样技术和选择合理的建议密度是同时采用的。

（3）选择合理的建议密度
基本粒子滤波的前提假设：重要性重采样能够从一个合理的后验建议密度分布中采样得到一组样本点集合，而且这组样本点集合能够很好地覆盖真实状态。如果这些假设条件不能满足，粒子滤波算法的效果就要下降；因此，如果能找到一个最优的建议密度分布函数，引导重采样做正确的采样分布，那么就能保证样本集合的有效性，也就保证了滤波的最终质量。

建议密度函数

介绍两种从建议密度函数的角度来改进粒子滤波算法的方法，分别用扩展卡尔曼EKF和无迹卡尔曼UKF来做建议密度函数，从而改进算法性能。

EPF算法

扩展卡尔曼是一种局部线性化的方法，它通过一阶泰勒展开式实现，它是一种递归的最小均方误差MMSE估计方法，要求系统是近似高斯后验分布模型。在粒子滤波算法框架下，EKF算法主要用于为每个粒子产生符合建议密度分布，称为扩展卡尔曼粒子滤波（EPF）。初始化-重要性采样-重采样-输出。

UPF算法

无迹卡尔曼滤波也是一种递归的最小均方误差估计，利用UKF来改进粒子滤波算法称为无迹卡尔曼粒子滤波（UPF）。初始化-重要性采样-重采样-输出。

UPF算法的误差较低，但计算时间较长。

算法实现

1.main.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 主函数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能说明：ekf,ukf,pf,epf,upf算法的综合比较程序
function main
 
rand('seed',3);
randn('seed',6);
%error('下面的参数T请参考书中的值设置，然后删除本行代码') 
T = 50;
R =  1e-5;              
                       
g1 = 3;                
g2 = 2;               
 
X = zeros(1,T);
Z = zeros(1,T);
processNoise = zeros(T,1);
measureNoise = zeros(T,1);
X(1) = 1;                         
P0 = 3/4;
 
Qekf=10*3/4;                
Rekf=1e-1;                    
Xekf=zeros(1,T);               
Pekf = P0*ones(1,T);         
Tekf=zeros(1,T);               

 
Qukf=2*3/4;                  
Rukf=1e-1;                    
Xukf=zeros(1,T);               
Pukf = P0*ones(1,T);          
Tukf=zeros(1,T);                

 
N=200;                      
Xpf=zeros(1,T);             
Xpfset=ones(T,N);         
Tpf=zeros(1,T);            

 
Xepf=zeros(1,T);           
Xepfset=ones(T,N);         
Pepf = P0*ones(T,N);          
Tepf=zeros(1,T);               

 
Xupf=zeros(1,T);            
Xupfset=ones(T,N);              
Pupf = P0*ones(T,N);       
Tupf=zeros(1,T);               
 
for t=2:T
    processNoise(t) =  gengamma(g1,g2);  
    measureNoise(t) =  sqrt(R)*randn;    
 
    X(t) = feval('ffun',X(t-1),t) +processNoise(t);
 
    Z(t) = feval('hfun',X(t),t) + measureNoise(t);
    
 
    tic
    [Xekf(t),Pekf(t)]=ekf(Xekf(t-1),Z(t),Pekf(t-1),t,Qekf,Rekf);
    Tekf(t)=toc;
    
 
    tic
    [Xukf(t),Pukf(t)]=ukf(Xukf(t-1),Z(t),Pukf(t-1),Qukf,Rukf,t);
    Tukf(t)=toc;
    
 
    tic
    [Xpf(t),Xpfset(t,:)]=pf(Xpfset(t-1,:),Z(t),N,t,R,g1,g2);
    Tpf(t)=toc;
    
 
    tic
    [Xepf(t),Xepfset(t,:),Pepf(t,:)]=epf(Xepfset(t-1,:),Z(t),t,Pepf(t-1,:),N,R,Qekf,Rekf,g1,g2);
    Tepf(t)=toc;
    
 
    tic
    [Xupf(t),Xupfset(t,:),Pupf(t,:)]=upf(Xupfset(t-1,:),Z(t),t,Pupf(t-1,:),N,R,Qukf,Rukf,g1,g2);
    Tupf(t)=toc;
end;
 
ErrorEkf=abs(Xekf-X); 
ErrorUkf=abs(Xukf-X);  
ErrorPf=abs(Xpf-X);     
ErrorEpf=abs(Xepf-X);   
ErrorUpf=abs(Xupf-X);   
 
figure
hold on;box on;
p1=plot(1:T,X,'-k.','lineWidth',2);
p2=plot(1:T,Xekf,'m:','lineWidth',2);
p3=plot(1:T,Xukf,'--','lineWidth',2);
p4=plot(1:T,Xpf,'-ro','lineWidth',2);
p5=plot(1:T,Xepf,'-g*','lineWidth',2);
p6=plot(1:T,Xupf,'-b^','lineWidth',2);
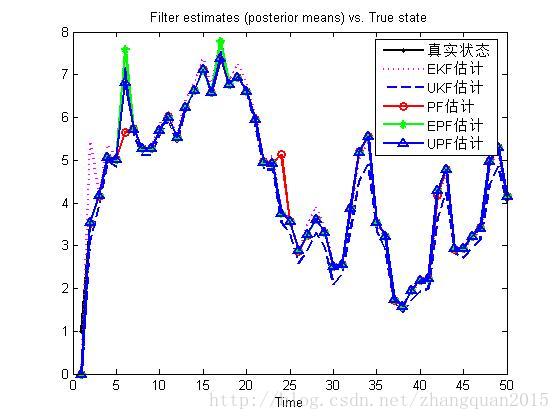
legend([p1,p2,p3,p4,p5,p6],'真实状态','EKF估计','UKF估计','PF估计','EPF估计','UPF估计')
xlabel('Time','fontsize',10)
title('Filter estimates (posterior means) vs. True state','fontsize',10)

 
figure
hold on;box on;
p1=plot(1:T,ErrorEkf,'-k.','lineWidth',2);
p2=plot(1:T,ErrorUkf,'-m^','lineWidth',2);
p3=plot(1:T,ErrorPf,'-ro','lineWidth',2);
p4=plot(1:T,ErrorEpf,'-g*','lineWidth',2);
p5=plot(1:T,ErrorUpf,'-bd','lineWidth',2);
legend([p1,p2,p3,p4,p5],'EKF偏差','UKF偏差','PF偏差','EPF偏差','UPF偏差')

 
figure
hold on;box on;
p1=plot(1:T,Tekf,'-k.','lineWidth',2);
p2=plot(1:T,Tukf,'-m^','lineWidth',2);
p3=plot(1:T,Tpf,'-ro','lineWidth',2);
p4=plot(1:T,Tepf,'-g*','lineWidth',2);
p5=plot(1:T,Tupf,'-bd','lineWidth',2);
legend([p1,p2,p3,p4,p5],'EKF时间','UKF时间','PF时间','EPF时间','UPF时间')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

2.ekf.m

function [Xekf,Pout]=ekf(Xin,Z,Pin,t,Qekf,Rekf)

Xpre=feval('ffun',Xin,t);
Jx=0.5;
 
Pekfpre = Qekf + Jx*Pin*Jx';
 
Zekfpre= feval('hfun',Xpre,t);
 
if t<=30
    Jy = 2*0.2*Xpre;
else
    Jy = 0.5;
end
 
M = Rekf + Jy*Pekfpre*Jy';
 
K = Pekfpre*Jy'*inv(M);
 
 
Xekf=Xpre+K*(Z-Zekfpre);
 
 
Pout = Pekfpre - K*Jy*Pekfpre;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

3.ukf.m

% 无迹卡尔曼滤波算法
function [Xout,Pout]=ukf(Xin,Z,Pin,Qukf,Rukf,t) 
alpha = 1;
beta  = 0;
kappa = 2;

states       = size(Xin(:),1);
observations = size(Z(:),1);
vNoise       = size(Qukf,2);
wNoise       = size(Rukf,2);
noises       = vNoise+wNoise;

 
if (noises)
    N=[Qukf zeros(vNoise,wNoise); zeros(wNoise,vNoise) Rukf];
    PQ=[Pin zeros(states,noises);zeros(noises,states) N];
    xQ=[Xin;zeros(noises,1)];
else
    PQ=Pin;
    xQ=Xin;
end;

 
[xSigmaPts, wSigmaPts, nsp] = scaledSymmetricSigmaPoints(xQ, PQ, alpha, beta, kappa);
 
wSigmaPts_xmat = repmat(wSigmaPts(:,2:nsp),states,1);
wSigmaPts_zmat = repmat(wSigmaPts(:,2:nsp),observations,1);

 
xPredSigmaPts = feval('ffun',xSigmaPts(1:states,:),t)+xSigmaPts(states+1:states+vNoise,:);
zPredSigmaPts = feval('hfun',xPredSigmaPts,t)+xSigmaPts(states+vNoise+1:states+noises,:);

 
xPred = sum(wSigmaPts_xmat .* (xPredSigmaPts(:,2:nsp) - repmat(xPredSigmaPts(:,1),1,nsp-1)),2);
zPred = sum(wSigmaPts_zmat .* (zPredSigmaPts(:,2:nsp) - repmat(zPredSigmaPts(:,1),1,nsp-1)),2);
xPred=xPred+xPredSigmaPts(:,1);
zPred=zPred+zPredSigmaPts(:,1);
 
exSigmaPt = xPredSigmaPts(:,1)-xPred;
ezSigmaPt = zPredSigmaPts(:,1)-zPred;

PPred   = wSigmaPts(nsp+1)*exSigmaPt*exSigmaPt';
PxzPred = wSigmaPts(nsp+1)*exSigmaPt*ezSigmaPt';
S       = wSigmaPts(nsp+1)*ezSigmaPt*ezSigmaPt';

exSigmaPt = xPredSigmaPts(:,2:nsp) - repmat(xPred,1,nsp-1);
ezSigmaPt = zPredSigmaPts(:,2:nsp) - repmat(zPred,1,nsp-1);
PPred     = PPred + (wSigmaPts_xmat .* exSigmaPt) * exSigmaPt';
S         = S + (wSigmaPts_zmat .* ezSigmaPt) * ezSigmaPt';
PxzPred   = PxzPred + exSigmaPt * (wSigmaPts_zmat .* ezSigmaPt)';

 
K  = PxzPred / S;

 
inovation = Z - zPred;

 
Xout = xPred + K*inovation;

 
Pout = PPred - K*S*K';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

4.pf.m

% 基本粒子滤波算法
function [Xo,Xoset]=pf(Xiset,Z,N,k,R,g1,g2)
 
tic
 
resamplingScheme=1;
 
Zpre=ones(1,N);   
Xsetpre=ones(1,N);  
w = ones(1,N);     

 
for i=1:N
    Xsetpre(i) = feval('ffun',Xiset(i),k) + gengamma(g1,g2);
end;

 
for i=1:N,
    Zpre(i) = feval('hfun',Xsetpre(i),k);
    w(i) = inv(sqrt(R)) * exp(-0.5*inv(R)*((Z-Zpre(i))^(2))) ...
        + 1e-99; 
end;
w = w./sum(w);             
 
if resamplingScheme == 1
    outIndex = residualR(1:N,w');       
elseif resamplingScheme == 2
    outIndex = systematicR(1:N,w');  
else
    outIndex = multinomialR(1:N,w');  
end;

 
Xoset = Xsetpre(outIndex); 
Xo=mean(Xoset);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

5.epf.m

% 用EKF改进的粒子滤波算法--EPF
% 用EKF产生建议分布
% 输入参数说明：
%    Xiset是上t-1时刻的粒子集合，Z是t时刻的观测
%    Pin对应Xiset粒子集合的方差\
% 输出参数说明：
%    Xo是epf算法最终的估计结果
%    Xoset是k时刻的粒子集合，其均值就是Xo
%    Pout是Xoset对应的方差
function [Xo,Xoset,Pout]=epf(Xiset,Z,t,Pin,N,R,Qekf,Rekf,g1,g2)
  
 
resamplingScheme=1;

 
Zpre=ones(1,N);     
Xsetpre=ones(1,N);   
w = ones(1,N);      

Pout=ones(1,N);      
Xekf=ones(1,N);     
Xekf_pre=ones(1,N); 

 
for i=1:N
 
    [Xekf(i),Pout(i)]=ekf(Xiset(i),Z,Pin(i),t,Qekf,Rekf);
 
    Xsetpre(i)=Xekf(i)+sqrtm(Pout(i))*randn;
end

 
for i=1:N,
  
    Zpre(i) = feval('hfun',Xsetpre(i),t);
 
    lik = inv(sqrt(R)) * exp(-0.5*inv(R)*((Z-Zpre(i))^(2)))+1e-99;
    prior = ((Xsetpre(i)-Xiset(i))^(g1-1)) * exp(-g2*(Xsetpre(i)-Xiset(i)));
    proposal = inv(sqrt(Pout(i))) * ...
        exp(-0.5*inv(Pout(i)) *((Xsetpre(i)-Xekf(i))^(2)));
    w(i) = lik*prior/proposal;
end;
 
w= w./sum(w);

 
if resamplingScheme == 1
    outIndex = residualR(1:N,w');   
elseif resamplingScheme == 2
    outIndex = systematicR(1:N,w');     
else
    outIndex = multinomialR(1:N,w');    
end;
 
Xoset = Xsetpre(outIndex);  
Pout = Pout(outIndex);      
 
Xo = mean(Xoset);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

6.upf.m

% 用UKF改进的粒子滤波算法--UPF
% 用UKF产生建议分布
% 输入参数说明：
%    Xiset是上t-1时刻的粒子集合，Z是t时刻的观测
%    Pin对应Xiset粒子集合的方差\
% 输出参数说明：
%    Xo是upf算法最终的估计结果
%    Xoset是k时刻的粒子集合，其均值就是Xo
%    Pout是Xoset对应的方差
function [Xo,Xoset,Pout]=upf(Xiset,Z,t,Pin,N,R,Qukf,Rukf,g1,g2)
 
resamplingScheme=1;

 
Xukf=ones(1,N);     
Xset_pre=ones(1,N);  
Zpre=ones(1,N); 
for i=1:N
 
    [Xukf(i),Pout(i)]=ukf(Xiset(i),Z,Pin(i),Qukf,Rukf,t);
  
    Xset_pre(i) = Xukf(i) + sqrtm(Pout(i))*randn;
end

 
for i=1:N
 
    Zpre(i) = feval('hfun',Xset_pre(i),t);
 
    lik = inv(sqrt(R)) * exp(-0.5*inv(R)*((Z-Zpre(i))^(2)))+1e-99;
    prior = ((Xset_pre(i)-Xiset(i))^(g1-1)) * exp(-g2*(Xset_pre(i)-Xiset(i)));
    proposal = inv(sqrt(Pout(i))) * ...
        exp(-0.5*inv(Pout(i)) *((Xset_pre(i)-Xukf(i))^(2)));
    w(i) = lik*prior/proposal;
end;
 
w = w./sum(w);

 
if resamplingScheme == 1
    outIndex = residualR(1:N,w');        
elseif resamplingScheme == 2
    outIndex = systematicR(1:N,w');      
else
    outIndex = multinomialR(1:N,w');     
end;

 
Xoset = Xset_pre(outIndex);  
Pout = Pout(outIndex);     
 
Xo = mean(Xoset);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

7.ffun.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 状态方程函数
function [y] = ffun(x,t);
 
if nargin < 2
    error('Not enough input arguments.'); 
end
beta = 0.5;
y = 1 + sin(4e-2*pi*t) + beta*x;

8.hfun.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 观测方程函数
function [y] = hfun(x,t);
 
if nargin < 2, 
    error('Not enough input arguments.');
end
if t<=30
    y = (x.^(2))/5;
else
    y = -2 + x/2;
end;

9.gengamma.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 产生一个符合gamma分布的噪声
function x = gengamma(alpha, beta)
 
if (alpha==1)
    x = -log(1-rand(1,1))/beta;
    return
end
flag=0;
if (alpha<1)  
    flag=1;
    alpha=alpha+1;
end
gamma=alpha-1;
eta=sqrt(2.0*alpha-1.0);
c=.5-atan(gamma/eta)/pi;
aux=-.5;
while(aux<0)
    y=-.5;
    while(y<=0)
        u=rand(1,1);
        y = gamma + eta * tan(pi*(u-c)+c-.5);
    end
    v=-log(rand(1,1));
    aux=v+log(1.0+((y-gamma)/eta)^2)+gamma*log(y/gamma)-y+gamma;
end;

 
if (flag==1) 
    x = y/beta*(rand(1))^(1.0/(alpha-1));
else
    x = y/beta;
end

10.scaledSymmetricSigmaPoints.m

function [xPts, wPts, nPts] = scaledSymmetricSigmaPoints(x,P,alpha,beta,kappa)
n    = size(x(:),1);
nPts = 2*n+1;           
kappa = alpha^2*(n+kappa)-n;
wPts=zeros(1,nPts);
xPts=zeros(n,nPts);
Psqrtm=(chol((n+kappa)*P))';  
xPts=[zeros(size(P,1),1) -Psqrtm Psqrtm];
xPts = xPts + repmat(x,1,nPts);  
wPts=[kappa 0.5*ones(1,nPts-1) 0]/(n+kappa);
wPts(nPts+1) = wPts(1) + (1-alpha^2) + beta;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

11.multinomialR.m

%% 多项式重采样
function outIndex = multinomialR(inIndex,q);
 
  error('下面的参数nargin请参考书中的值设置，然后删除本行代码') 
if nargin < 0, error('Not enough input arguments.'); end

[S,arb] = size(q);  

 
N_babies= zeros(1,S);
cumDist= cumsum(q');   
 
u = fliplr(cumprod(rand(1,S).^(1./(S:-1:1))));
j=1;
for i=1:S
  while (u(1,i)>cumDist(1,j))
    j=j+1;
  end
  N_babies(1,j)=N_babies(1,j)+1;
end;
 
index=1;
for i=1:S
  if (N_babies(1,i)>0)
    for j=index:index+N_babies(1,i)-1
      outIndex(j) = inIndex(i);
    end;
  end;   
  index= index+N_babies(1,i);   
end

12.residualR.m

%% 随机重采样
function outIndex = residualR(inIndex,q);
if nargin < 2, error('Not enough input arguments.'); end

[S,arb] = size(q); 
 
N_babies= zeros(1,S);
 
q_res = S.*q';  
N_babies = fix(q_res);
 
N_res=S-sum(N_babies);
if (N_res~=0)
  q_res=(q_res-N_babies)/N_res;
  cumDist= cumsum(q_res);   
   
  u = fliplr(cumprod(rand(1,N_res).^(1./(N_res:-1:1))));
  j=1;
  for i=1:N_res
    while (u(1,i)>cumDist(1,j))
      j=j+1;
    end
    N_babies(1,j)=N_babies(1,j)+1;
  end;
end;

 
index=1;
for i=1:S
  if (N_babies(1,i)>0)
    for j=index:index+N_babies(1,i)-1
      outIndex(j) = inIndex(i);
    end;
  end;   
  index= index+N_babies(1,i);   
end

13.systematicR.m

%% 系统重采样
function outIndex = systematicR(inIndex,wn);
 
  error('下面的参数nargin 请参考书中的值设置，然后删除本行代码')  
if nargin < 0, error('Not enough input arguments.'); end

wn=wn';
[arb,N] = size(wn);   

 

N_children=zeros(1,N);
label=zeros(1,N);
label=1:1:N;

s=1/N;
auxw=0;
auxl=0;
li=0;   
T=s*rand(1);
j=1;
Q=0;
i=0;

 
u=rand(1,N);
while (T<1)
   if (Q>T)
      T=T+s;
      N_children(1,li)=N_children(1,li)+1;
   else
 
      i=fix((N-j+1)*u(1,j))+j;
 
      auxw=wn(1,i);
      li=label(1,i);
 
      Q=Q+auxw;
 
      wn(1,i)=wn(1,j);
      label(1,i)=label(1,j);
   
      j=j+1;
   end
end
 
index=1;
for i=1:N
  if (N_children(1,i)>0)
    for j=index:index+N_children(1,i)-1
      outIndex(j) = inIndex(i);
    end;
  end;   
  index= index+N_children(1,i);   
end

此博客均属原创或译文，欢迎转载但请注明出处
Github个人博客：https://joeyos.github.io