- 如何在 Fork 的 GitHub 项目中保留自己的修改并同步上游更新?github_fork_update
iBaoxing
github
如何在Fork的GitHub项目中保留自己的修改并同步上游更新?在GitHub上Fork了一个项目后,你可能会对项目进行一些修改,同时原作者也在不断更新。如果想要在保留自己修改的基础上,同步原作者的最新更新,很多人会不知所措。本文将详细讲解如何在不丢失自己改动的情况下,将上游仓库的更新合并到自己的仓库中。问题描述假设你在GitHub上Fork了一个项目,并基于该项目做了一些修改,随后你发现原作者对
- html 中如何使用 uniapp 的部分方法
某公司摸鱼前端
htmluni-app前端
示例代码:Documentconsole.log(window);效果展示:好了,现在就可以uni.使用相关的方法了
- 腾讯云技术深度探索:构建高效云原生微服务架构
我的运维人生
云原生架构腾讯云运维开发技术共享
腾讯云技术深度探索:构建高效云原生微服务架构在当今快速发展的技术环境中,云原生技术已成为企业数字化转型的关键驱动力。腾讯云作为行业领先的云服务提供商,不断推出创新的产品和技术,助力企业构建高效、可扩展的云原生微服务架构。本文将深入探讨腾讯云在微服务领域的最新进展,并通过一个实际案例展示如何在腾讯云平台上构建云原生应用。腾讯云微服务架构概览腾讯云微服务架构基于云原生理念,旨在帮助企业快速实现应用的容
- Pyecharts数据可视化大屏:打造沉浸式数据分析体验
我的运维人生
信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏:打造沉浸式数据分析体验在当今这个数据驱动的时代,如何将海量数据以直观、生动的方式展现出来,成为了数据分析师和企业决策者关注的焦点。Pyecharts,作为一款基于Python的开源数据可视化库,凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力,成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏,并通过实际代码案例
- Google earth studio 简介
陟彼高冈yu
旅游
GoogleEarthStudio是一个基于Web的动画工具,专为创作使用GoogleEarth数据的动画和视频而设计。它利用了GoogleEarth强大的三维地图和卫星影像数据库,使用户能够轻松地创建逼真的地球动画、航拍视频和动态地图可视化。网址为https://www.google.com/earth/studio/。GoogleEarthStudio是一个基于Web的动画工具,专为创作使用G
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
- DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
- 少了生活气息
我爱大草莓
最近啊,总觉得自己日更的内容缺了点什么。我仔细地想,大概是少了些生活气息。这两三个月减少了许多与别人相处的时间,独自生活,偶尔只是出去买菜,总觉得生活好像变空了许多。买菜的时候会跟档口的阿姨聊一两句话,让自己感觉在真实地生活着。幸好我也不是一宅到底,偶尔周末也会约着跟好朋友见面,面对面交流跟隔着屏幕交流,效果还是不一样的,至少有更为真实的生活感。写作不仅需要有阅读量,有文笔,生活阅历也是非常重要的
- 深入理解 MultiQueryRetriever:提升向量数据库检索效果的强大工具
nseejrukjhad
数据库python
深入理解MultiQueryRetriever:提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域,高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用,但仍存在一些局限性。本文将介绍一种创新的解决方案:MultiQueryRetriever,它通过自动生成多个查询视角来增强检索效果,提高结果的相关性和多样性。MultiQueryRetriever的工
- 在一台Ubuntu计算机上构建Hyperledger Fabric网络
落叶无声9
区块链超级账本Hyperledgerfabric区块链ubuntu构建hyperledgerfabric
在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台,为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时,我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件,部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
- Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
- 基于CODESYS的多轴运动控制程序框架:逻辑与运动控制分离,快速开发灵活操作
GPJnCrbBdl
python开发语言
基于codesys开发的多轴运动控制程序框架,将逻辑与运动控制分离,将单轴控制封装成功能块,对该功能块的操作包含了所有的单轴控制(归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等)。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式,程序状态的跳转都已完成,只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义,能帮助开发者快速
- 基于Python给出的PDF文档转Markdown文档的方法
程序媛了了
pythonpdf开发语言
注:网上有很多将Markdown文档转为PDF文档的方法,但是却很少有将PDF文档转为Markdown文档的方法。就算有,比如某些网站声称可以将PDF文档转为Markdown文档,尝试过,不太符合自己的要求,而且无法保证文档没有泄露风险。于是本人为了解决这个问题,借助GPT(能使用GPT镜像或者有条件直接使用GPT的,反正能调用GPT接口就行)生成Python代码来完成这个功能。笔记、代码难免存在
- BART&BERT
Ambition_LAO
深度学习
BART和BERT都是基于Transformer架构的预训练语言模型。模型架构:BERT(BidirectionalEncoderRepresentationsfromTransformers)主要是一个编码器(Encoder)模型,它使用了Transformer的编码器部分来处理输入的文本,并生成文本的表示。BERT特别擅长理解语言的上下文,因为它在预训练阶段使用了掩码语言模型(MLM)任务,即
- (121)DAC接口--->(006)基于FPGA实现DAC8811接口
FPGA系统设计指南针
FPGA接口开发(项目实战)fpga开发FPGAIC
1目录(a)FPGA简介(b)IC简介(c)Verilog简介(d)基于FPGA实现DAC8811接口(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电
- esp32开发快速入门 8 : MQTT 的快速入门,基于esp32实现MQTT通信
z755924843
ESP32开发快速入门服务器网络运维
MQTT介绍简介MQTT(MessageQueuingTelemetryTransport,消息队列遥测传输协议),是一种基于发布/订阅(publish/subscribe)模式的"轻量级"通讯协议,该协议构建于TCP/IP协议上,由IBM在1999年发布。MQTT最大优点在于,可以以极少的代码和有限的带宽,为连接远程设备提供实时可靠的消息服务。作为一种低开销、低带宽占用的即时通讯协议,使其在物联
- vue项目element-ui的table表格单元格合并
酋长哈哈
vue.jselementuijavascript前端
一、合并效果二全部代码exportdefault{name:'CellMerge',data(){return{tableData:[{id:'1',name:'王小虎',amount1:'165',amount2:'3.2',amount3:10},{id:'1',name:'王小虎',amount1:'162',amount2:'4.43',amount3:12},{id:'1',name:'
- python批量读取tiff文件_Python Pillow批量转换tif格式到jpg
weixin_39557797
最近因为想要整下网站的壁纸,从网站下载了别人整理好的合集压缩包,解压之后,却发现里面的文件都是tif的,tif格式网站和电脑都不认的,根本不能作壁纸。这时候,就需要转换图片格式了,首先我找了几款转换格式的软件,发现效果都不好,要不是不支持tif格式,要不就是转换出来的图片糊的不行。最终,还是决定用Python的Pillow库来写一个脚本,完成这个任务。下面是整个的小脚本----importosim
- android 更改窗口的层次,浮窗开发之窗口层级
Ms.Bu
android更改窗口的层次
最近在项目中遇到了这样的需求:需要在特定的其他应用之上悬浮自己的UI交互(拖动、输入等复杂的UI交互),和九游的浮窗类似,不过我们的比九游的体验更好,我们越过了很多授权的限制。浮窗效果很多人都知道如何去实现一个简单的浮窗,但是却很少有人去深入的研究背后的流程机制,由于项目中浮窗交互比较复杂,遇到了些坑查看了很多资料,故总结浮窗涉及到的知识点:窗口层级关系(浮窗是如何“浮”的)?浮窗有哪些限制,如何
- 2023-06-19【感恩日记】第246篇
o泡沫o
思想日记:坚持下去,相信自己一定可以的【感恩日记】第246篇1.我真是太幸福啦!感恩孩子早起阅读,放学到学生之家完成作业,平安度过美好的一天。感恩!感恩!感恩!❤️2.我真是太幸福啦!感恩自己早起给孩子煮早餐,完成计划的工作,晚上学习。感恩!感恩!感恩!❤️3.我真是太幸福啦!感恩为我设计效果图的老师。感恩!感恩!感恩!❤️4.我真是太幸福啦!感恩父母养育了我,有妈的孩子真幸福。感恩!感恩!感恩!
- 06选课支付模块之基于消息队列发送支付通知消息
echo 云清
学成在线javarabbitmq消息队列支付通知学成在线
消息队列发送支付通知消息需求分析订单服务作为通用服务,在订单支付成功后需要将支付结果异步通知给其他对接的微服务,微服务收到支付结果根据订单的类型去更新自己的业务数据技术方案使用消息队列进行异步通知需要保证消息的可靠性即生产端将消息成功通知到服务端:消息发送到交换机-->由交换机发送到队列-->消费者监听队列,收到消息进行处理,参考文章02-使用Docker安装RabbitMQ-CSDN博客生产者确
- 摄影小白,怎么才能拍出高大上产品图片?
是波妞唉
很多人以为文案只要会码字,会排版就OK了!说实话,没接触到这一行的时候,我的想法更简单,以为只要会写字就行!可是真做了文案才发现,码字只是入门级的基本功。一篇文章离不开排版、配图,说起来很简单!从头做到尾你就会发现,写文章用两个小时,找合适的配图居然要花掉半天的时间,甚至更久!图片能找到合适的就不怕,还有找不到的,比如产品图,只能亲自拍。拿着摆弄了半天,就是拍不出想要的效果,光线不好、搭出来丑破天
- 基于STM32与Qt的自动平衡机器人:从控制到人机交互的的详细设计流程
极客小张
stm32qt机器人物联网人机交互毕业设计c语言
一、项目概述目标和用途本项目旨在开发一款基于STM32控制的自动平衡机器人,结合步进电机和陀螺仪传感器,实现对平衡机器人的精确控制。该机器人可以用于教育、科研、娱乐等多个领域,帮助用户了解自动控制、机器人运动学等相关知识。技术栈关键词STM32单片机步进电机陀螺仪传感器AD采集电路Qt人机界面实时数据监控二、系统架构系统架构设计本项目的系统架构设计包括以下主要组件:控制单元:STM32单片机传感器
- 基于STM32的汽车仪表显示系统:集成CAN、UART与I2C总线设计流程
极客小张
stm32汽车嵌入式硬件物联网单片机c语言
一、项目概述项目目标与用途本项目旨在设计和实现一个基于STM32微控制器的汽车仪表显示系统。该系统能够实时显示汽车的速度、转速、油量等关键信息,并通过CAN总线与其他汽车控制单元进行通信。这种仪表显示系统不仅提高了驾驶的安全性和便捷性,还能为汽车提供更智能的用户体验。技术栈关键词微控制器:STM32显示技术:TFTLCD/OLED传感器:速度传感器、温度传感器、油量传感器通信协议:CAN总线、UA
- Python多线程实现大规模数据集高效转移
sand&wich
网络python服务器
背景在处理大规模数据集时,通常需要在不同存储设备、不同服务器或文件夹之间高效地传输数据。如果采用单线程传输方式,当数据量非常大时,整个过程会非常耗时。因此,通过多线程并行处理可以大幅提升数据传输效率。本文将分享一个基于Python多线程实现的高效数据传输工具,通过遍历源文件夹中的所有文件,将它们移动到目标文件夹。工具和库这个数据集转移工具主要依赖于以下Python标准库:os:用于文件系统操作,如
- 阅读《别说你懂思维导图》21~23章day27
Ling宝尔
合理期待——思维导图的应用效果很多人问我,思维导图真的有用么?我常常回答,如果你觉得是它“没用”,一定是因为你没“用”,有“用”才“有用”。实际上,学习思维导图和学习木工、驾驶等技能型学习一样,都要经历从了解到应用、从应用到受益的过程。在使用前,我们很多人的思维处于“无意识的低效”状态,经过一段时间的学习,虽然掌握了思维导图的基本使用方法,但可能并没有太好的效果,这个阶段可称为“有意识的低效”状态
- ESP32-C3入门教程 网络篇⑩——基于esp_https_ota和MQTT实现开机主动升级和被动触发升级的OTA功能
小康师兄
ESP32-C3入门教程https服务器esp32OTAMQTT
文章目录一、前言二、软件流程三、部分源码四、运行演示一、前言本文基于VSCodeIDE进行编程、编译、下载、运行等操作基础入门章节请查阅:ESP32-C3入门教程基础篇①——基于VSCode构建HelloWorld教程目录大纲请查阅:ESP32-C3入门教程——导读ESP32-C3入门教程网络篇⑨——基于esp_https_ota实现史上最简单的ESP32OTA远程固件升级功能二、软件流程
- 冬练太极虽好,也需做好防护!
武当功夫传人郑师和
俗话说,夏练三伏,冬练三九,练功绝非一日之功,必须持之以恒。太极拳是一项集文化、养生、锻炼于一体的活动。现在已经进入冬季,许多喜爱太极拳的朋友们仍然会到户外进行锻炼。这种精神固然可嘉,但是也一定要注意一些相关事项,以避免影响养生的效果。冬季练拳要“养汗”太极拳一日不练十日空,入冬天冷以后要“守汗”,春生夏长秋收冬藏,冬天练功,万物冬藏,要养阳气,需要藏精,顺天时天利,盘拳时,身体微热要见汗,还没出
- 项目:事半功倍的法宝
小小效能
行动的三大流程:记录、排程和执行,也讲了易效能的4D原则以及T-step标签法。这些流程和方法能够解决我们眼前的一地鸡毛,让我们有更多时间和精力去关注更为长远的事情,完成工作、生活和人生中重要的项目。项目管理能够让我们围绕结果去做事情,达成事半功倍的效果,也就是做更少的事情,但达成更好的效果。如果我们能够不断地达成一个又一个的项目,那么我们的人生无疑会像滚雪球一样,在长坡道上面不断积累。一、项目的
- 对股票分析时要注意哪些主要因素?
会飞的奇葩猪
股票 分析 云掌股吧
众所周知,对散户投资者来说,股票技术分析是应战股市的核心武器,想学好股票的技术分析一定要知道哪些是重点学习的,其实非常简单,我们只要记住三个要素:成交量、价格趋势、振荡指标。
一、成交量
大盘的成交量状态。成交量大说明市场的获利机会较多,成交量小说明市场的获利机会较少。当沪市的成交量超过150亿时是强市市场状态,运用技术找综合买点较准;
- 【Scala十八】视图界定与上下文界定
bit1129
scala
Context Bound,上下文界定,是Scala为隐式参数引入的一种语法糖,使得隐式转换的编码更加简洁。
隐式参数
首先引入一个泛型函数max,用于取a和b的最大值
def max[T](a: T, b: T) = {
if (a > b) a else b
}
因为T是未知类型,只有运行时才会代入真正的类型,因此调用a >
- C语言的分支——Object-C程序设计阅读有感
darkblue086
applec框架cocoa
自从1972年贝尔实验室Dennis Ritchie开发了C语言,C语言已经有了很多版本和实现,从Borland到microsoft还是GNU、Apple都提供了不同时代的多种选择,我们知道C语言是基于Thompson开发的B语言的,Object-C是以SmallTalk-80为基础的。和C++不同的是,Object C并不是C的超集,因为有很多特性与C是不同的。
Object-C程序设计这本书
- 去除浏览器对表单值的记忆
周凡杨
html记忆autocompleteform浏览
&n
- java的树形通讯录
g21121
java
最近用到企业通讯录,虽然以前也开发过,但是用的是jsf,拼成的树形,及其笨重和难维护。后来就想到直接生成json格式字符串,页面上也好展现。
// 首先取出每个部门的联系人
for (int i = 0; i < depList.size(); i++) {
List<Contacts> list = getContactList(depList.get(i
- Nginx安装部署
510888780
nginxlinux
Nginx ("engine x") 是一个高性能的 HTTP 和 反向代理 服务器,也是一个 IMAP/POP3/SMTP 代理服务器。 Nginx 是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的,第一个公开版本0.1.0发布于2004年10月4日。其将源代码以类BSD许可证的形式发布,因它的稳定性、丰富的功能集、示例配置文件和低系统资源
- java servelet异步处理请求
墙头上一根草
java异步返回servlet
servlet3.0以后支持异步处理请求,具体是使用AsyncContext ,包装httpservletRequest以及httpservletResponse具有异步的功能,
final AsyncContext ac = request.startAsync(request, response);
ac.s
- 我的spring学习笔记8-Spring中Bean的实例化
aijuans
Spring 3
在Spring中要实例化一个Bean有几种方法:
1、最常用的(普通方法)
<bean id="myBean" class="www.6e6.org.MyBean" />
使用这样方法,按Spring就会使用Bean的默认构造方法,也就是把没有参数的构造方法来建立Bean实例。
(有构造方法的下个文细说)
2、还
- 为Mysql创建最优的索引
annan211
mysql索引
索引对于良好的性能非常关键,尤其是当数据规模越来越大的时候,索引的对性能的影响越发重要。
索引经常会被误解甚至忽略,而且经常被糟糕的设计。
索引优化应该是对查询性能优化最有效的手段了,索引能够轻易将查询性能提高几个数量级,最优的索引会比
较好的索引性能要好2个数量级。
1 索引的类型
(1) B-Tree
不出意外,这里提到的索引都是指 B-
- 日期函数
百合不是茶
oraclesql日期函数查询
ORACLE日期时间函数大全
TO_DATE格式(以时间:2007-11-02 13:45:25为例)
Year:
yy two digits 两位年 显示值:07
yyy three digits 三位年 显示值:007
- 线程优先级
bijian1013
javathread多线程java多线程
多线程运行时需要定义线程运行的先后顺序。
线程优先级是用数字表示,数字越大线程优先级越高,取值在1到10,默认优先级为5。
实例:
package com.bijian.study;
/**
* 因为在代码段当中把线程B的优先级设置高于线程A,所以运行结果先执行线程B的run()方法后再执行线程A的run()方法
* 但在实际中,JAVA的优先级不准,强烈不建议用此方法来控制执
- 适配器模式和代理模式的区别
bijian1013
java设计模式
一.简介 适配器模式:适配器模式(英语:adapter pattern)有时候也称包装样式或者包装。将一个类的接口转接成用户所期待的。一个适配使得因接口不兼容而不能在一起工作的类工作在一起,做法是将类别自己的接口包裹在一个已存在的类中。 &nbs
- 【持久化框架MyBatis3三】MyBatis3 SQL映射配置文件
bit1129
Mybatis3
SQL映射配置文件一方面类似于Hibernate的映射配置文件,通过定义实体与关系表的列之间的对应关系。另一方面使用<select>,<insert>,<delete>,<update>元素定义增删改查的SQL语句,
这些元素包含三方面内容
1. 要执行的SQL语句
2. SQL语句的入参,比如查询条件
3. SQL语句的返回结果
- oracle大数据表复制备份个人经验
bitcarter
oracle大表备份大表数据复制
前提:
数据库仓库A(就拿oracle11g为例)中有两个用户user1和user2,现在有user1中有表ldm_table1,且表ldm_table1有数据5千万以上,ldm_table1中的数据是从其他库B(数据源)中抽取过来的,前期业务理解不够或者需求有变,数据有变动需要重新从B中抽取数据到A库表ldm_table1中。
- HTTP加速器varnish安装小记
ronin47
http varnish 加速
上午共享的那个varnish安装手册,个人看了下,有点不知所云,好吧~看来还是先安装玩玩!
苦逼公司服务器没法连外网,不能用什么wget或yum命令直接下载安装,每每看到别人博客贴出的在线安装代码时,总有一股羡慕嫉妒“恨”冒了出来。。。好吧,既然没法上外网,那只能麻烦点通过下载源码来编译安装了!
Varnish 3.0.4下载地址: http://repo.varnish-cache.org/
- java-73-输入一个字符串,输出该字符串中对称的子字符串的最大长度
bylijinnan
java
public class LongestSymmtricalLength {
/*
* Q75题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
* 比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
*/
public static void main(String[] args) {
Str
- 学习编程的一点感想
Cb123456
编程感想Gis
写点感想,总结一些,也顺便激励一些自己.现在就是复习阶段,也做做项目.
本专业是GIS专业,当初觉得本专业太水,靠这个会活不下去的,所以就报了培训班。学习的时候,进入状态很慢,而且当初进去的时候,已经上到Java高级阶段了,所以.....,呵呵,之后有点感觉了,不过,还是不好好写代码,还眼高手低的,有
- [能源与安全]美国与中国
comsci
能源
现在有一个局面:地球上的石油只剩下N桶,这些油只够让中国和美国这两个国家中的一个顺利过渡到宇宙时代,但是如果这两个国家为争夺这些石油而发生战争,其结果是两个国家都无法平稳过渡到宇宙时代。。。。而且在战争中,剩下的石油也会被快速消耗在战争中,结果是两败俱伤。。。
在这个大
- SEMI-JOIN执行计划突然变成HASH JOIN了 的原因分析
cwqcwqmax9
oracle
甲说:
A B两个表总数据量都很大,在百万以上。
idx1 idx2字段表示是索引字段
A B 两表上都有
col1字段表示普通字段
select xxx from A
where A.idx1 between mmm and nnn
and exists (select 1 from B where B.idx2 =
- SpringMVC-ajax返回值乱码解决方案
dashuaifu
AjaxspringMVCresponse中文乱码
SpringMVC-ajax返回值乱码解决方案
一:(自己总结,测试过可行)
ajax返回如果含有中文汉字,则使用:(如下例:)
@RequestMapping(value="/xxx.do") public @ResponseBody void getPunishReasonB
- Linux系统中查看日志的常用命令
dcj3sjt126com
OS
因为在日常的工作中,出问题的时候查看日志是每个管理员的习惯,作为初学者,为了以后的需要,我今天将下面这些查看命令共享给各位
cat
tail -f
日 志 文 件 说 明
/var/log/message 系统启动后的信息和错误日志,是Red Hat Linux中最常用的日志之一
/var/log/secure 与安全相关的日志信息
/var/log/maillog 与邮件相关的日志信
- [应用结构]应用
dcj3sjt126com
PHPyii2
应用主体
应用主体是管理 Yii 应用系统整体结构和生命周期的对象。 每个Yii应用系统只能包含一个应用主体,应用主体在 入口脚本中创建并能通过表达式 \Yii::$app 全局范围内访问。
补充: 当我们说"一个应用",它可能是一个应用主体对象,也可能是一个应用系统,是根据上下文来决定[译:中文为避免歧义,Application翻译为应
- assertThat用法
eksliang
JUnitassertThat
junit4.0 assertThat用法
一般匹配符1、assertThat( testedNumber, allOf( greaterThan(8), lessThan(16) ) );
注释: allOf匹配符表明如果接下来的所有条件必须都成立测试才通过,相当于“与”(&&)
2、assertThat( testedNumber, anyOf( g
- android点滴2
gundumw100
应用服务器android网络应用OSHTC
如何让Drawable绕着中心旋转?
Animation a = new RotateAnimation(0.0f, 360.0f,
Animation.RELATIVE_TO_SELF, 0.5f, Animation.RELATIVE_TO_SELF,0.5f);
a.setRepeatCount(-1);
a.setDuration(1000);
如何控制Andro
- 超简洁的CSS下拉菜单
ini
htmlWeb工作html5css
效果体验:http://hovertree.com/texiao/css/3.htmHTML文件:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>简洁的HTML+CSS下拉菜单-HoverTree</title>
- kafka consumer防止数据丢失
kane_xie
kafkaoffset commit
kafka最初是被LinkedIn设计用来处理log的分布式消息系统,因此它的着眼点不在数据的安全性(log偶尔丢几条无所谓),换句话说kafka并不能完全保证数据不丢失。
尽管kafka官网声称能够保证at-least-once,但如果consumer进程数小于partition_num,这个结论不一定成立。
考虑这样一个case,partiton_num=2
- @Repository、@Service、@Controller 和 @Component
mhtbbx
DAOspringbeanprototype
@Repository、@Service、@Controller 和 @Component 将类标识为Bean
Spring 自 2.0 版本开始,陆续引入了一些注解用于简化 Spring 的开发。@Repository注解便属于最先引入的一批,它用于将数据访问层 (DAO 层 ) 的类标识为 Spring Bean。具体只需将该注解标注在 DAO类上即可。同时,为了让 Spring 能够扫描类
- java 多线程高并发读写控制 误区
qifeifei
java thread
先看一下下面的错误代码,对写加了synchronized控制,保证了写的安全,但是问题在哪里呢?
public class testTh7 {
private String data;
public String read(){
System.out.println(Thread.currentThread().getName() + "read data "
- mongodb replica set(副本集)设置步骤
tcrct
javamongodb
网上已经有一大堆的设置步骤的了,根据我遇到的问题,整理一下,如下:
首先先去下载一个mongodb最新版,目前最新版应该是2.6
cd /usr/local/bin
wget http://fastdl.mongodb.org/linux/mongodb-linux-x86_64-2.6.0.tgz
tar -zxvf mongodb-linux-x86_64-2.6.0.t
- rust学习笔记
wudixiaotie
学习笔记
1.rust里绑定变量是let,默认绑定了的变量是不可更改的,所以如果想让变量可变就要加上mut。
let x = 1; let mut y = 2;
2.match 相当于erlang中的case,但是case的每一项后都是分号,但是rust的match却是逗号。
3.match 的每一项最后都要加逗号,但是最后一项不加也不会报错,所有结尾加逗号的用法都是类似。
4.每个语句结尾都要加分
![]() are spectra. Provided that
are spectra. Provided that ![]() is optimal, then the minimum mean-square error equation reduces to
is optimal, then the minimum mean-square error equation reduces to![]() is the inverse two-sided Laplace transform of
is the inverse two-sided Laplace transform of ![]() .
.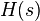 consists of the causal part of
consists of the causal part of 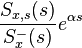 (that is, that part of this fraction having a positive time solution under the inverse Laplace transform)
(that is, that part of this fraction having a positive time solution under the inverse Laplace transform)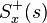 is the causal component of
is the causal component of 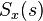 (i.e., the inverse Laplace transform of
(i.e., the inverse Laplace transform of 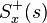 is non-zero only for
is non-zero only for 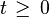 )
)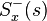 is the anti-causal component of
is the anti-causal component of 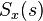 (i.e., the inverse Laplace transform of
(i.e., the inverse Laplace transform of 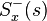 is non-zero only for
is non-zero only for 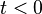 )
)![]() in a specific case, one should follow these steps:[2]
in a specific case, one should follow these steps:[2]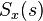 in rational form and factor it into causal and anti-causal components:
in rational form and factor it into causal and anti-causal components:
 contains all the zeros and poles in the left half plane (LHP) and
contains all the zeros and poles in the left half plane (LHP) and 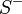 contains the zeroes and poles in the right half plane (RHP). This is called the Wiener–Hopf factorization.
contains the zeroes and poles in the right half plane (RHP). This is called the Wiener–Hopf factorization.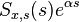 by
by 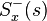 and write out the result as a partial fraction expansion.
and write out the result as a partial fraction expansion.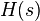 .
.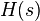 by
by 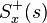 . The result is the desired filter transfer function
. The result is the desired filter transfer function 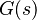 .
.
