算法之排序（三）

  这次主要谈谈大名鼎鼎的快速排序。

快速排序其实也是分治算法的一种应用，它将数组分为两个子数组，然后分别将数组排序，当子数组有序时整个数组也就有序了。在归并排序中，数组被均分为两部分，而在快速排序中切分（partition）取决于数组中的内容。快速排序递归的将子数组a[lo...hi]排序，先用partition()方法将a[j]放到合适的位置，然后再用递归调用将其他元素排序。而快速排序的关键在于切分，这个过程使得数组满足下列条件：

 1.对于某个j，a[j]已经排定；

 2.a[lo]到a[j-1]中的所有元素都不大于a[j];

 3.a[j+1]到a[hi]中的所有元素都不小于a[j]。

 要实现这个方法一般策略是先随意的取a[lo]作为切分元素，即那个将会被排定的元素，然后我们从数组的左端开始扫描直到找到一个大于等于它的元素，再从数组的右端开始找到一个小于等于它的元素。这两个元素显然是没有排定的，因此交换他们的位置，如此继续，就可以保证左指针i的左侧元素都不大于切分元素，右指针j右侧的元素都不小于切分元素。当两个指针相遇时，我们只需要将切分元素a[lo]和左子数组最右侧的元素（a[j]）交换然后返回j即可。

 时间复杂度的讨论：将长度为N的无重复数组排序，快速排序平均需要2NlnN次比较（以及1/6的交换）。快速排序最多需要约N^2/2次比较，但随即打乱能够预防这种情况。（可以使用C++的algorithm库中shuffle函数来进行打乱序列。具体的用法可以Google）

下面给出快速排序的各个方法具体实现代码：

//切分数组
template
int partition(T array[], int lo, int hi) {
    int i = lo;
    int j = hi + 1;
    T v = array[lo];
    while (true) {
        while (array[++i] < v) {
            if (i == hi) {
                break;
            }
        }
        while (v < array[--j]) {
            if (j == lo) {
                break;
            }
        }
        if (i >= j) {
            break;
        }
        std::swap(array[i], array[j]);
    }
    std::swap(array[lo], array[j]);
    return j;
}

//快速排序的递归主程序
template
void qsort_(T array[], int lo, int hi) {
    if (lo >= hi) return;
    int j = partition(array, lo, hi);
    qsort_(array, lo, j - 1);
    qsort_(array, j + 1, hi);
}
//对外提供的接口
template
void quick_sort(T array[], int length) {
    qsort_(array, 0, length - 1);
}

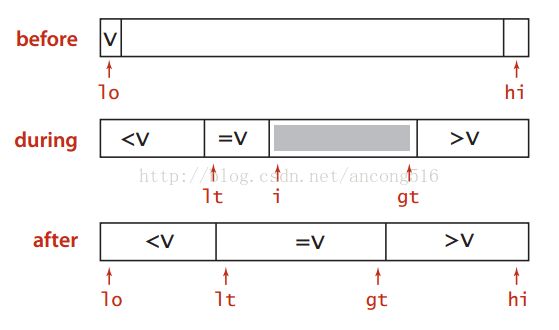
快速排序对于小数组的优势其实并不明显，可以考虑再数组元素小于20时改用插入排序。下面再考虑一种改进方法，名为“三向切分的快速排序”，它从左向右遍历数组一次，维护一个指针lt使得a[lo...lt-1]中的所有元素都小于v，一个指针gt使得a[gt+1...hi]中的所有元素都大于v，一个指针i使得a[lt...i-1]中的元素都等于v。

下面给出“三向切分快速排序的递归例程”：

//三向切分的快速排序
template
void qsort_3way_(T array[], int lo, int hi) {
    if (hi <= lo) return;
    int lt = lo, i = lo + 1, gt = hi;
    T v = array[lo];
    while (i <= gt) {
        if (array[i] < v) {
            std::swap(array[lt++], array[i++]);
        } else if (array[i] > v) {
            std::swap(array[i], array[gt--]);
        } else {
            i++;
        }
    }
    qsort_3way_(array, lo, lt - 1);
    qsort_3way_(array, gt + 1, hi);
}

时间复杂度分析：

  对于大小为N的数组，三向切分的快速排序需要(2ln2)NH次比较，其中H是主键值出现的频率定义的香农信息量。

其实对于标准的快速排序，随着数组规模的增大其运行时间会趋于平均运行时间。对于包含大量重复元素的数组，三向切分快速排序将时间复杂度从线性对数级降到线性级别。快速排序已经在计算机界得到了广泛使用。说到这里，很多人以为排序算法到这里就结束了，其实不然，排序其实不一定要建立在比较的基础上，后面还会讨论这些巧妙的排序算法。