最短路的四种求法详解+模板
欢迎访问https://blog.csdn.net/lxt_Lucia~~
宇宙第一小仙女\(^o^)/~~萌量爆表求带飞=≡Σ((( つ^o^)つ~dalao们点个关注呗~~
一.最短路之Floyd算法
Floyd算法虽然时间复杂度不是最短的,但是代码是最简单的最短的啦~
1.介绍
floyd算法只有五行代码,代码简单,三个for循环就可以解决问题,所以它的时间复杂度为O(n^3),可以求多源最短路问题。
2.思想:
Floyd算法的基本思想如下:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点X到B。所以,我们假设Dis(AB)为节点A到节点B的最短路径的距离,对于每一个节点X,我们检查Dis(AX) + Dis(XB) < Dis(AB)是否成立,如果成立,证明从A到X再到B的路径比A直接到B的路径短,我们便设置Dis(AB) = Dis(AX) + Dis(XB),这样一来,当我们遍历完所有节点X,Dis(AB)中记录的便是A到B的最短路径的距离。
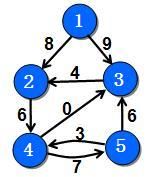
举个例子:已知下图,
如现在只允许经过1号顶点,求任意两点之间的最短路程,只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点,再从1号顶点到j号顶点的路程之和。其中i是1~n循环,j也是1~n循环,代码实现如下。
for(i=1; i<=n; i++)
{
for(j=1; j<=n; j++)
{
if ( e[i][j] > e[i][1]+e[1][j] )
e[i][j] = e[i][1]+e[1][j];
}
}接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。在只允许经过1号顶点时任意两点的最短路程的结果下,再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小,代码实现为如下。
//经过1号顶点
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if (e[i][j] > e[i][1]+e[1][j])
e[i][j]=e[i][1]+e[1][j];
//经过2号顶点
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if (e[i][j] > e[i][2]+e[2][j])
e[i][j]=e[i][2]+e[2][j];最后允许通过所有顶点作为中转,代码如下:
for(k=1; k<=n; k++)
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if(e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。与上面相同
3.代码模板:
#include
#define inf 0x3f3f3f3f
int map[1000][1000];
int main()
{
int k,i,j,n,m;
//读入n和m,n表示顶点个数,m表示边的条数
scanf("%d %d",&n,&m);
//初始化
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if(i==j)
map[i][j]=0;
else
map[i][j]=inf;
int a,b,c;
//读入边
for(i=1; i<=m; i++)
{
scanf("%d %d %d",&a,&b,&c);
map[a][b]=c;//这是一个有向图
}
//Floyd-Warshall算法核心语句
for(k=1; k<=n; k++)
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if(map[i][j]>map[i][k]+map[k][j] )
map[i][j]=map[i][k]+map[k][j];
//输出最终的结果,最终二维数组中存的即使两点之间的最短距离
for(i=1; i<=n; i++)
{
for(j=1; j<=n; j++)
{
printf("%10d",map[i][j]);
}
printf("\n");
}
return 0;
}
二.最短路之Bellman-Ford算法
1.说明:
Dijkstra算法是处理单源最短路径的有效算法,但它局限于边的权值非负的情况,若图中出现权值为负的边,Dijkstra算法就会失效,求出的最短路径就可能是错的。
这时候,就需要使用其他的算法来求解最短路径,Bellman-Ford算法就是其中最常用的一个。
2.适用条件&范围:
单源最短路径(从源点s到其它所有顶点v);
有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);
边权可正可负(如有负权回路输出错误提示);
3.思想:
我们规定节点都有一个key值,key值记录的是开始节点到本节点的最小距离,每个节点也都有一个p指针指向他的前驱节点。这里我们规定一个操作叫做松弛操作,我们的算法也是最终基于这个操作的。松弛操作就是去更新key的值。
![]()
节点B的key值为8,表示从开始节点到B节点之前的最短估计距离是8,而节点A的key值3,是说从开始节点到A节点最短估计是3,当我们发现这个边时,从A到B的距离比较近,所以我们去更新B的key值,同时把B的前驱节点设置成A。这个过程就是松弛操作。
我们说的Bellman-Ford算法是最简单的算法,就是从开始节点开始循环每一条边,对他进行松弛操作。最后得到的路径就是最短路径。过程如图:
![]()
4.算法步骤:
1.初始化:将除源点外的所有顶点的最短距离估计值 d[v] ← +∞, d[s] ←0;
2.迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
3.检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中
#include
#include
using namespace std;
#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点,边,起点
typedef struct Edge //边
{
int u, v;
int cost;
} Edge;
Edge edge[N];
int dis[N], pre[N];
bool Bellman_Ford()
{
int ok;
for(int i = 1; i <= nodenum; ++i) //初始化,起点本身赋值为0,其余赋值为最大
dis[i] = (i == original ? 0 : MAX);
for(int i = 1; i <= nodenum - 1; ++i)
{
ok=1;
for(int j = 1; j <= edgenum; ++j)
if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛(顺序一定不能反)
{
dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
pre[edge[j].v] = edge[j].u;//这里用来存储路径
ok=0;
}
if(ok==1) //优化这里,如果这趟没跟新任何节点就可以直接退出了。
break;
}
bool flag = 1; //判断是否含有负权回路
for(int i = 1; i <= edgenum; ++i)
if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
{
flag = 0;
break;
}
return flag;
}
void print_path(int root) //打印最短路的路径(反向)
{
while(root != pre[root]) //前驱
{
printf("%d-->", root);
root = pre[root];
}
if(root == pre[root])
printf("%d\n", root);
}
int main()
{
scanf("%d%d%d", &nodenum, &edgenum, &original);//输入点边起点,一般起点规定为1
pre[original] = original;//为了输出最短路用的,前驱为本身
for(int i = 1; i <= edgenum; ++i)
{
scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);//有向图
}
if(Bellman_Ford())//如果没有负权
for(int i = 1; i <= nodenum; ++i) //每个点最短路
{
printf("%d\n", dis[i]);
printf("Path:");
print_path(i);
}
else
printf("have negative circle\n");
return 0;
}
三.最短路之dijkstra算法
1.定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
2.算法描述
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
执行动画过程如下图
![]()
动图太快可以看下面的例子:
![]()
重点需要理解这句拗口的”按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度”
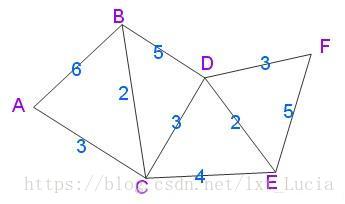
实际上,Dijkstra算法是一个排序过程,就上面的例子来说,是根据A到图中其余点的最短路径长度进行排序,路径越短越先被找到,路径越长越靠后才能被找到,要找A到F的最短路径,我们依次找到了
A–> C 的最短路径3
A–> C –> B 的最短路径5
A–> C –> D 的最短路径6
A–> C –> E 的最短路径7
A–> C –> D –> F 的最短路径9
3.解释说明
为什么Dijkstra算法不适用于带负权的图?
就上个例子来说,当把一个点选入集合S时,就意味着已经找到了从A到这个点的最短路径,比如第二步,把C点选入集合S,这时已经找到A到C的最短路径了,但是如果图中存在负权边,就不能再这样说了。举个例子,假设有一个点Z,Z只与A和C有连接,从A到Z的权为50,从Z到C的权为-49,现在A到C的最短路径显然是A–> Z –> C
再举个例子:
![]()
在这个图中,求从A到C的最短路,如果用Dijkstra根据贪心的思想,选择与A最接近的点C,长度为7,以后不再变化。但是很明显此图最短路为5。归结原因是Dijkstra采用贪心思想,不从整体考虑结果,只从当前情况考虑选择最优。
4.代码模板
#include
#include
using namespace std;
#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点,边,起点
typedef struct Edge //边
{
int u, v;
int cost;
} Edge;
Edge edge[N];
int dis[N], pre[N];
bool Bellman_Ford()
{
int ok;
for(int i = 1; i <= nodenum; ++i) //初始化,起点本身赋值为0,其余赋值为最大
dis[i] = (i == original ? 0 : MAX);
for(int i = 1; i <= nodenum - 1; ++i)
{
ok=1;
for(int j = 1; j <= edgenum; ++j)
if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛(顺序一定不能反)
{
dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
pre[edge[j].v] = edge[j].u;//这里用来存储路径
ok=0;
}
if(ok==1) //优化这里,如果这趟没跟新任何节点就可以直接退出了。
break;
}
bool flag = 1; //判断是否含有负权回路
for(int i = 1; i <= edgenum; ++i)
if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
{
flag = 0;
break;
}
return flag;
}
void print_path(int root) //打印最短路的路径(反向)
{
while(root != pre[root]) //前驱
{
printf("%d-->", root);
root = pre[root];
}
if(root == pre[root])
printf("%d\n", root);
}
int main()
{
scanf("%d%d%d", &nodenum, &edgenum, &original);//输入点边起点,一般起点规定为1
pre[original] = original;//为了输出最短路用的,前驱为本身
for(int i = 1; i <= edgenum; ++i)
{
scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);//有向图
}
if(Bellman_Ford())//如果没有负权
for(int i = 1; i <= nodenum; ++i) //每个点最短路
{
printf("%d\n", dis[i]);
printf("Path:");
print_path(i);
}
else
printf("have negative circle\n");
return 0;
}
5.用vector实现dijkstra代码
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
struct node
{
int end;//终点
int power;//权值
} t;
int n;//n为边数
vectorq[500001];//邻接表存储图的信息
int dis[500001];//距离数组
bool vis[500001];//标记数组
void Dijkstra(int start, int end)
{
memset(vis, false, sizeof(vis));
for(int i=0; i<=n; i++)
{
dis[i] = INF;
}
int len=q[start].size();
for(int i=0; iq[pos][j].power+dis[pos] )
dis[q[pos][j].end ] = q[pos][j].power + dis[pos];
}
}
printf("%d\n", dis[end] );
}
int main()
{
int m;
while(scanf("%d %d", &n, &m)&&n&&m)//输入点和边
{
for(int i=0; i<=n; i++)
q[i].clear();//将vector数组清空
for(int i=0; i
四.SPFA算法(最快最便捷咯~)
求单源最短路的SPFA算法的全称是:Shortest Path Faster Algorithm。
SPFA算法是西南交通大学段凡丁于1994年发表的。
从名字我们就可以看出,这种算法在效率上一定有过人之处。
很多时候,给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便派上用场了。有人称spfa算法是最短路的万能算法。
简洁起见,我们约定有向加权图G不存在负权回路,即最短路径一定存在。当然,我们可以在执行该算法前做一次拓扑排序,以判断是否存在负权回路。
我们用数组dis记录每个结点的最短路径估计值,可以用邻接矩阵或邻接表来存储图G,推荐使用邻接表。
1.spfa的算法思想(动态逼近法):
设立一个先进先出的队列q用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
松弛操作的原理是著名的定理:“三角形两边之和大于第三边”,在信息学中我们叫它三角不等式。所谓对结点i,j进行松弛,就是判定是否dis[j]>dis[i]+w[i,j],如果该式成立则将dis[j]减小到dis[i]+w[i,j],否则不动。
下面举一个实例来说明SFFA算法是怎样进行的:
2.和广搜bfs的区别:
SPFA 在形式上和广度(宽度)优先搜索非常类似,不同的是bfs中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是一个点改进过其它的点之后,过了一段时间可能本身被改进(重新入队),于是再次用来改进其它的点,这样反复迭代下去。
3.算法的描述:
void spfa(s); //求单源点s到其它各顶点的最短距离
for i=1 to n do { dis[i]=∞; vis[i]=false; } //初始化每点到s的距离,不在队列
dis[s]=0; //将dis[源点]设为0
vis[s]=true; //源点s入队列
head=0; tail=1; q[tail]=s; //源点s入队, 头尾指针赋初值
while headdis[v]+a[v][i]) //如果不满足三角形性质
dis[i] = dis[v] + a[v][i] //松弛dis[i]
if (vis[i]=false) {tail+1; q[tail]=i; vis[i]=true;} //不在队列,则加入队列
}
4.最短路径本身怎么输出?
在一个图中,我们仅仅知道结点A到结点E的最短路径长度,有时候意义不大。这个图如果是地图的模型的话,在算出最短路径长度后,我们总要说明“怎么走”才算真正解决了问题。如何在计算过程中记录下来最短路径是怎么走的,并在最后将它输出呢?
我们定义一个path[]数组,path[i]表示源点s到i的最短路程中,结点i之前的结点的编号(父结点),我们在借助结点u对结点v松弛的同时,标记下path[v]=u,记录的工作就完成了。
如何输出呢?我们记录的是每个点前面的点是什么,输出却要从最前面到后面输出,这很好办,递归就可以了:
void printpath(int k){
if (path[k]!=0) printpath(path[k]);
cout << k << ' ';
}
pascal code:
procedure printpath(k:longint);
begin
if path[k]<>0 then printpath(path[k]);
write(k,' ');
end;
spfa算法模板(邻接矩阵):
c++ code:
void spfa(int s){
for(int i=0; i<=n; i++) dis[i]=99999999; //初始化每点i到s的距离
dis[s]=0; vis[s]=1; q[1]=s; 队列初始化,s为起点
int i, v, head=0, tail=1;
while (head0 && dis[i]>dis[v]+a[v][i]){
dis[i] = dis[v]+a[v][i]; 修改最短路
if (vis[i]==0){ 如果扩展结点i不在队列中,入队
tail++;
q[tail]=i;
vis[i]=1;
}
}
}
}
pascal code:
procedure spfa(s:longint);
var i,j,v,head,tail:longint;
begin
for i:=0 to n do dis[i]:=99999999;
dis[s]:=0; vis[s]:=true; q[1]:=s;
head:=0;tail:= 1;
while headdis[v]+a[v,i] then
begin
dis[i]:= dis[v]+a[v,i];
if not vis[i] then
begin
inc(tail);
q[tail]:=i;
vis[i]:=true;
end;
end;
end;
end;
5.HINT:对于最短路,可以用Dijkstra或者SPFA算法来实现,这个简单。
问题是如何去遍历这些点,找到任意两点间最短的那一条。
首先要明白,在用Dijkstra或者SPFA算法求解最短路时,不但可以求出任意一点到源点的最短路,它还可以被用来求解一个集合到另一个集合间的最短路。
(集合间的最短路的定义:对于其中一个集合的任一点到另一个集合中的任一点中的最短路径中最短的一条。)
如何求?
很简单,只需要把一个集合里所有的点的dis数组初值赋为0。这样集合里的任意一点到其它点的距离都为0,等价于把集合里所有点认为是一个点x,这样最后求出来的dis数组里存的就是另一个集合里的每一个点到点x的最短路,再找出dis数组里最小的路径,即为集合间的最短路。
现在我们知道了如何求集合间的最短路,那么问题就变成了把k个点划分成两个集合,然后求集合间的最短路。可是每次划分集合,要保证任意两个点之间的最短路都能求到,这样时间复杂度又是巨大的未知数。
下面就是这个问题最关键的地方:二进制划分集合。
对于每一组数,按照他们的二进制从低位到高位划分,把当前位上为1的数放到一个集合里,为0的放到另一个集合。这样就保证了划分之后,任意两个点都会匹配到,当然可能会重复,不过在大问题里,这种小问题可忽略不计,不影响总体的时间复杂度。
数据最大为1e5,在经过这样的划分之后,最多划分17次就能求解出答案。
在划分完集合之后,问题就变得很简单,只需要每次划分集合后,一个集合作为起点另一个集合作为终点,跑一遍SPFA,然后反过来再跑一遍SPFA。每次找到最小值即为答案。
例题可参考:https://blog.csdn.net/Akatsuki__Itachi/article/details/79965636
6.spfa优化——深度优先搜索dfs
在上面的spfa标准算法中,每次更新(松弛)一个结点u时,如果该结点不在队列中,那么直接入队。
但是有负环时,上述算法的时间复杂度退化为O(nm)。能不能改进呢?
那我们试着使用深搜,核心思想为每次从更新一个结点u时,从该结点开始递归进行下一次迭代。
使用dfs优化spfa算法:
pascal code:
procedure spfa(s:longint);
var i:longint;
begin
for i:=1 to b[s,0] do //b[s,0]是从顶点s发出的边的条数
if dis[b[s,i]]>dis[s]+a[s,b[s,i]] then //b[s,i]是从s发出的第i条边的另一个顶点
begin
dis[b[s,i]]:=dis[s]+a[s,b[s,i]];
spfa(b[s,i]);
end;
end;
C++ code:
void spfa(int s){
for(int i=1; i<=b[s][0]; i++) //b[s,0]是从顶点s发出的边的条数
if (dis[b[s][i]>dis[s]+a[s][b[s][i]]){ //b[s,i]是从s发出的第i条边的另一个顶点
dis[b[s][i]=dis[s]+a[s][b[s][i]];
spfa(b[s][i]);
}
}
判断存在负环的条件:重新经过某个在当前搜索栈中的结点。
7.spfa优化——前向星优化
星形(star)表示法的思想与邻接表表示法的思想有一定的相似之处。对每个结点,它也是记录从该结点出发的所有弧,但它不是采用单向链表而是采用一个单一的数组表示。也就是说,在该数组中首先存放从结点1出发的所有弧,然后接着存放从节点2出发的所有孤,依此类推,最后存放从结点n出发的所有孤。对每条弧,要依次存放其起点、终点、权的数值等有关信息。这实际上相当于对所有弧给出了一个顺序和编号,只是从同一结点出发的弧的顺序可以任意排列。此外,为了能够快速检索从每个节点出发的所有弧,我们一般还用一个数组记录每个结点出发的弧的起始地址(即弧的编号)。在这种表示法中,可以快速检索从每个结点出发的所有弧,这种星形表示法称为前向星形(forward star)表示法。
例如,在下图中,仍然假设弧(1,2),(l,3),(2,4),(3,2),(4,3),(4,5),(5,3)和(5,4)上的权分别为8,9,6,4,0,7,6和3。此时该网络图可以用前向星形表示法表示如下:
前向星存储图:
#include
using namespace std;
int first[10005];
struct edge{
int point,next,len;
} e[10005];
void add(int i, int u, int v, int w){
e[i].point = v;
e[i].next = first[u];
e[i].len = w;
first[u] = i;
}
int n,m;
int main(){
int u,v,w;
cin >> n >> m;
for (int i = 1; i <= m; i++){
cin >> u >> v >> w;
add(i,u,v,w);
} //这段是读入和加入
for (int i = 0; i <= n; i++){
cout << "from " << i << endl;
for (int j = first[i]; j; j = e[j].next) //这就是遍历边了
cout << "to " << e[j].point << " length= " << e[j].len << endl;
}
}
以上便是最短路的四种算法,所涉及的参考资料有:
http://www.cnblogs.com/aiguona/p/7226446.html
https://www.cnblogs.com/aiguona/p/7226533.html
http://www.cnblogs.com/aiguona/p/7226341.html
http://www.cnblogs.com/aiguona/p/7229189.html
https://blog.csdn.net/xunalove/article/details/70045815
https://blog.csdn.net/Akatsuki__Itachi/article/details/79965636