基于慢特征分析(Slow Feature Analysis, SFA)的变化检测方法

前段时间阅读了两篇利用慢特征分析进行变化检测的论文，其中一篇是利用慢特征分析进行变化检测，另一篇则是在前一篇提出的算法的基础上进行相对辐射校正。下面对这一基于慢特征分析的变化检测方法进行介绍。

1 慢特征分析

慢特征分析(slow feature analysis, SFA)是一种非监督学习方法,它可以从时间序列中提取变化缓慢的特征。在数学上，SFA可以表示成为一个最优化问题，在保持信号信息量的前提下，最小化输出信号的变化频率。
给定一个n维的时序输入信号$[x_1(t),x_2(t),...,x_n(t)]$ ，SFA旨在找到一组函数$[g_1(x),g_2(x),...,g_M(x)]$ ，通过这组函数得到输出信号 ，这些信号变化得尽可能慢但是又包含了重要的信息。SFA的线性模型可以写成如下形式：
$$min{\Delta }_j=\Delta (z_j)=<\dot{z_j^2}>$$

$$s.t.\{\begin{array}{c}<z_j{>}_t=0\\ <z_j^2{>}_t=1\\ \forall i<j,<z_i{z}_j{>}_t=0\end{array}$$

$<\cdot {>}_t$ 表示序列的期望，$\dot{z}$表示时序差分，在线性的情况下，$g_j(x)=w_j^{T}x$ 。
我们对x进行中心化，这样即可满足约束(1)，目标函数和后两个约束可重写为
$$\Delta (z_j)=<\dot{z_j^2}{>}_t=<(w_j^T\dot{x}{)}^2{>}_t=w_j^T<\dot{x}{\dot{x}}^T{>}_t{w}_j=w_j^{T}A{w}_j$$

$$<z_j^2{>}_t=<(w_j^{T}x{)}^2{>}_t=w_j^T<x{x}^T{>}_t{w}_j=w_j^{T}B{w}_j$$

$$<z_i{z}_j{>}_t=<(w_i^{T}x{)}^2{>}_t=w_i^T<x{x}^T{>}_t{w}_j=w_i^{T}B{w}_j$$

将约束(2)加入目标函数(1)中，则目标函数可以重写为
$$\Delta (z_j)=\frac{w_j^{T}A{w}_j}{w_j^{T}B{w}_j}$$

这个优化问题可以转化为一个广义特征值问题
$$AW=BW\Lambda$$

其中W是广义特征向量组成的矩阵，广义特征向量即为$w_j$，$\Lambda$是广义特征值组成的对角矩阵且$\Delta (z_j)={\lambda }_j$。
慢特征的顺序由特征值的顺序决定，最慢的输出信号$\Delta (z_1)<\Delta (z_2)<\cdots <\Delta (z_N)$具有最小的特征值${\lambda }_1<{\lambda }_2<\cdots <{\lambda }_N$。

2 遥感慢特征分析理论

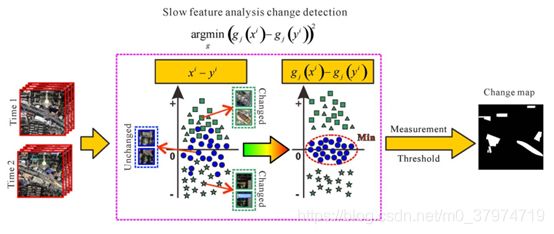
遥感慢特征分析理论能够在多时相遥感影像数据中提取不变特征，减小未变化像素的辐射差异，提高变化像素和未变化像素之间的可分性。利用遥感慢特征分析理论进行变化检测的原理如图2.1所示。

图2.1 基于SFA的变化检测原理

在原始的光谱空间中，由于辐射差异的存在，未变化像素的差值不等于0。变化像素和未变化像素之间的可分性也不够高。SFA变化检测旨在寻找一个新的特征空间，在新的空间中，未变化像素的差值最小，从而更好地突出变化区域。
和原始的SFA不同，在变化检测问题中不存在连续的时间序列结构，因此基于SFA的变化检测技术可以重新表达为如下形式。
给定一对同一位置的光谱向量$x^i=[x_1^i(t),x_2^i(t),...,x_n^i(t)]$和$y^i=[y_1^i(t),y_2^i(t),...,y_n^i(t)]$,首先对其进行标准化
$$x_j^i=\frac{x_j^i-{\mu }_{x_j}}{{\sigma }_{x_j}}and{y}_j^i=\frac{y_j^i-{\mu }_{y_j}}{{\sigma }_{y_j}}$$

然后SFA的线性模型可以重写成如下形式:
$$min\frac{1}{P}\sum _{i=1}^P{\left(g_j(x^i)-g_j(y^i)\right)}^2$$

$$s.t.\{\begin{array}{c}\frac{1}{2P}\left[{\sum }_{i=1}^P{g}_j(x^i)+{\sum }_{i=1}^P{g}_j(y^i)\right]=0\\ \frac{1}{2P}\left[{\sum }_{i=1}^P{g}_j^2(x^i)+{\sum }_{i=1}^P{g}_j^2(y^i)\right]=1\\ \forall i<l,\frac{1}{2P}\left[{\sum }_{i=1}^P{g}_j(x^i)g_l(x^i)+{\sum }_{i=1}^P{g}_j(y^i)g_l(y^i)\right]=0\end{array}$$

A和B可以表示为
$$A=\frac{1}{P}\sum _{i=1}^P\left(x^i-y^i\right){\left(x^i-y^i\right)}^T={\Sigma }_{\Delta }$$

$$B=\frac{1}{2P}\left[\sum _{i=1}^P\left(x^i\right){\left(x^i\right)}^T+\sum _{i=1}^P\left(y^i\right){\left(y^i\right)}^T\right]=\frac{1}{2}\left({\Sigma }_x+{\Sigma }_y\right)$$

优化问题可以表示为
$$\frac{w_j^{T}A{w}_j}{w_j^{T}B{w}_j}=\frac{w_j^T{\Sigma }_{\Delta }{w}_j}{w_j^T\frac{1}{2}\left({\Sigma }_x+{\Sigma }_y\right)w_j}$$

优化问题可以转化为广义特征值问题
$${\Sigma }_{\Delta }W=\frac{1}{2}\left({\Sigma }_x+{\Sigma }_y\right)W\Lambda$$

求解即可得到投影矩阵W。最终SFA变量可以由下式计算
$$SFA=W^{T}x-W^{T}y$$

本质上来说，遥感慢特征分析就是希望能够寻找到一组函数，在包含大量信息的同时，令投影后的不变特征差值有着最小的方差。
根据上述遥感慢特征分析理论，论文中具体提出了三种变化检测算法，分别是非监督慢特征分析(USFA)、监督慢特征分析(SSFA)和迭代慢特征分析(ISFA)。
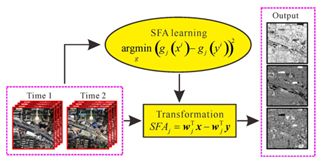
USFA是将整个多时相遥感影像作为输入来学习投影矩阵，所以如果真实变化相较于整个影像而言并不是特别异常，真实变化就会明显影响投影矩阵，使变化检测精度降低。

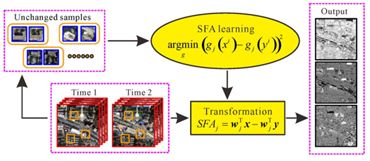
SSFA则是从影像上人工选取未变化像元作为训练样本来学习投影矩阵，与USFA相比，SSFA能够应用到常规变化检测问题中，但是SSFA需要大量有代表性的未变化样本，这些样本必须尽量包含所有类型的未变化地物。

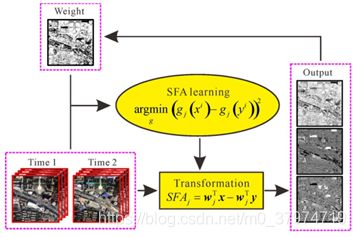
ISFA的基本思想和IRMAD相似，通过迭代定权的方式，令未变化像素在计算中越来越重要，变化像素在计算中的影响越来越小，从而学习到最佳的投影矩阵。

由于SFA变量是X和Y的线性组合，根据中心极限定理，SFA变量近似满足正态分布，因此SFA变量的平方除以方差之和服从自由度为p的卡方分布
$$T_j=\sum _{i=1}^P\left(\frac{SF{A}_{ij}^2}{\lambda }\right)\in {\chi }^2\left(p\right)$$

根据$T_j$即可判断各个像素是否发生变化。
ISFA就是在USFA的基础上根据$T_j$距离进行加权迭代
$$w_j=P\left\{T_j>t\right\}=P\left\{{\chi }^2\left(p\right)>T_j\right\}$$

然后让$w_j$参与到下一次的均值、方差以及矩阵A、B的计算中
$$\overline{X_i}=\frac{{\sum }_{j=1}^N{w}_j{X}_{ji}}{{\sum }_{j=1}^N{w}_j}$$

$$S_{kl}=\frac{{\sum }_{j=1}^N{w}_j\left(X_{jk}-\overline{X_k}\right)\left(X_{jl}-\overline{X_l}\right)}{(N-1){\sum }_{j=1}^N{w}_j/N}$$

$$A=\frac{{\sum }_{i=1}^P{w}^i\left(x^i-y^i\right){\left(x^i-y^i\right)}^T}{{\sum }_{i=1}^P{w}^i}$$

$$B=\frac{1}{2{\sum }_{i=1}^P{w}^i}\left[\sum _{i=1}^P{w}^i\left(x^i\right){\left(x^i\right)}^T+\sum _{i=1}^P{w}^i\left(y^i\right){\left(y^i\right)}^T\right]$$

得到A、B后根据广义特征值问题求解得到投影矩阵，接着继续计算$T_j$和$w_j$，反复迭代直到$\lambda$收敛。

3 基于ISFA的相对辐射校正

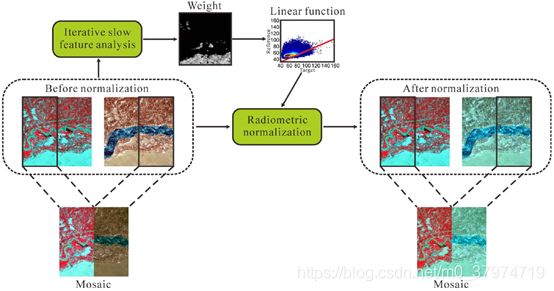
在第二节ISFA部分我们提到，ISFA算法通过迭代定权的方式，令未变化像素在计算中越来越重要，变化像素在计算中的影响越来越小，从而学习到最佳的投影矩阵，因此变化像素最终的权值会接近0，而不变的像素的权值将接近1。而相对辐射校正需要提取两景影像中伪不变特征(Pseudo-Invariant Features, PIFs)，利用PIFs计算两景影像的线性关系从而完成相对辐射校正。
在论文[2]这篇文章中，作者提出了一种基于ISFA的相对辐射自动校正算法，将ISFA得到的权值结果直接参与到相对辐射校正中。对于变化区域在影像中所占比重较大情况，作者在ISFA的基础上提出了基于初始种子的ISFA的相对辐射校正算法(S-ISFA)，通过给少部分变化区域赋权为1作为初始种子，使得算法可以很好的用于变化区域在影像中所占比重较大情况，并且实验结果显示最终的迭代结果并不依赖于初始种子的选取。
算法的具体流程如下：

1. 对多时相遥感影像X和Y进行赋权，如果无初始种子，则初始权重均为1，如果有初始种子，则将初始种子权值赋为1，其余像素赋为0。
2. 对X和Y进行ISFA，判断特征值 是否收敛，如果不收敛则继续迭代，如果收敛，进行Step 3。
3. 将ISFA得到的权重系数用于计算X和Y的线性关系，得到线性回归系数。
4. 根据线性回归系数和计算校正后的影像 。

4 实验

4.1 SFA

利用Python实现了USFA和ISFA，SSFA由于涉及到样本选取，没有进行实现。算法实现完成后在泰州2000年和2003年的两幅TM遥感影像上进行了实验。
USFA算法在泰州数据上的6个SFA波段如图4.1.1所示。

图4.1.1 USFA 6个波段

图中非常亮的或者非常暗的区域代表变化、灰色区域代表未变化。可以看出在前四个波段，变化区域从未变化区域中被分离出来，后两个波段只包含少量变化信息。
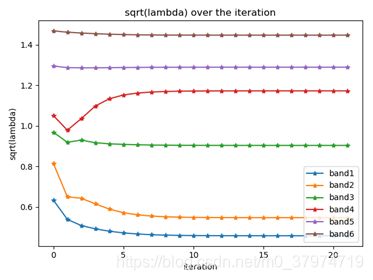
ISFA算法运行了23轮收敛，$\sqrt{\lambda }$迭代趋势如图4.1.2所示。

图4.1.2 sqrt(lambda)迭代趋势

ISFA算法在泰州数据上的6个SFA波段如图4.1.3所示。

图4.1.3 ISFA 6个波段

图中非常亮的或者非常暗的区域代表变化、灰色区域代表未变化。可以看出变化的区域在前三个波段被很好地从未变化地物中分离出来。同时ISFA提取的变化信息要优于USFA。
由于$T_j$包含了6个波段的信息，利用K-means算法对$T_j$进行阈值分割，得到bianry change map如图4.1.4所示。

图4.1.4 binary change map based on K-means(a为USFA，b为ISFA)

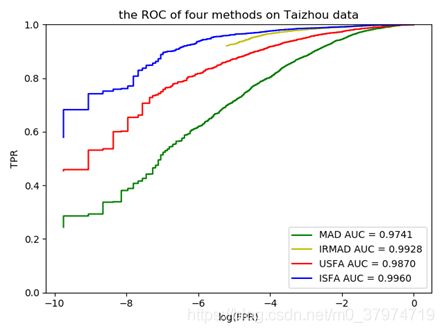
利用ROC曲线将SFA算法和MAD算法进行比较，如图4.1.5所示。

图4.1.5 四种方法的ROC曲线和AUC

从ROC曲线和计算得到的AUC可以看出MAD算法和SFA算法都是非常好的非监督变化检测算法，它们都可以达到很高的精度。相比较而言，SFA算法的结果要略优于MAD算法：USFA的精度要高于MAD算法，ISFA算法的迭代结果也要略优于IRMAD算法。

4.2 相对辐射校正

论文中提到，相对辐射校正有三种线性回归方程，分别是LSR, NR和OR，实验结果显示LSR的效果最好，因此在实验过程中均采用LSR。
对泰州的数据进行相对辐射校正，校正的目标影像为2000年，参考影像为2003年。校正前后第一波段的数据和参考影像如图4.2.1所示。

图4.2.1 目标影像和参考影像的第一波段数据(a为校正前2000TM, b为校正后2000TM, c为2003TM)

由于大气、照明条件、太阳高度角等条件的不同，可以看出校正前a和c在整体色调上存在明显的差异，a整体的灰度值更大，显得更亮。而经过相对辐射校正后，b在整体灰度上和c更为接近，而对于未变化的区域，如影像的四个角点区域，两影像灰度基本一致。
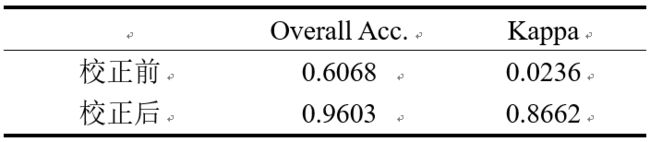
在论文[3]中作者提出了一种基于PCA和K-means的变化检测方法，在泰州数据上PCA&K-means算法得到的结果很差，kappa系数只有0.02，现在对泰州数据进行了相对辐射校正后，在校正后的数据上运行该算法，得到binary change map如图4.2.2所示。

图4.2.2 PCA&K-means算法的binary change map(a为校正前的结果，b为校正后的结果)

从binary change map中我们可以看出未进行相对辐射校正时，由于辐射差异的存在，算法把影像中间大片未变化的区域判定为变化区域，而对于影像右侧的那条道路却判定为未变化，可以看出PCA&K-means算法并不具有仿射无关性。
相对辐射校正前后的精度见表4.2.1。

表4.2.1 校正前后算法的精度

链接

论文[1] Slow Feature Analysis for Change Detection in Multispectral Imagery https://ieeexplore.ieee.org/document/6553145
论文[2] Automatic Radiometric Normalization for Multitemporal Remote Sensing Imagery with ISFA https://ieeexplore.ieee.org/document/6737226
论文[3] Unsupervised Change Detection in Satellite Images Using Principal Component Analysis and k-Means Clustering https://ieeexplore.ieee.org/document/5196726